黄冈市高二月考试卷
图片预览



文档简介
红安三中、大赵家高中高二联考数学试卷(文)
参考公式:
用最小二乘法求线性回归方程系数公式
P(K2≥k0)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
一、选择题(本大题共12小题,每小题5分,共60分.在每小题的四个选项中,只有一项符合题目要求.)
1.复数的共轭复数是 ( )
A. B. C. D.
2.已知x与y之间的一组数据:
x
0
1
2
3
y
1
3
5
7
则y与x的线性回归方程为必过点 ( )
A .(2,2) B.(1,2) C.(1.5,0) D.(1.5,4)
3.用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是 ( )
A.假设三内角都不大于60度; B.假设三内角都大于60度;
C.假设三内角至多有一个大于60度; D.假设三内角至多有两个大于60度
4.下列表述正确的是 ( )
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理。
A.①②③ B.②③④ C.②④⑤ D.①③⑤
5.若 ( )
A. B. C.6 D.8
6.在复平面内,复数对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.在下列表格中,每格填上一个数字后,使每一行
成等差数列,每一列成等比数列,则a+b+c的值是( )
1
?
2
?
?
0.5
?
1
?
?
?
?
a
?
?
?
?
?
b
?
?
?
?
?
c
A. 1 B. 2
C. 3 D. 4
8.从装有除颜色外完全相同的2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的两个事件是( ).
A.至少有1个白球,都是白球 B.至少有1个白球,至少有1个红球
C.恰有1个白球,恰有2个白球 D.至少有1个白球,都是红球
9.现有五个球分别记为A,C,J,K,S,随机放进三个盒子,每个盒子只能放一个球,则K或S在盒中的概率是( )
A. B. C. D.
10.从{a,b,c,d,e}的所有子集中任取一个,这个集合恰是集合{a,b,c}的子集的概率是( )
A. B. C. D.
11. 给出下列命题
(1)实数的共轭复数一定是实数;
(2)复数与其共轭复数的差是纯虚数:
(3)若,则
其中正确命题的序号是( )
A B C D
12.在区间上随机取一个数x,的值介于0到之间的概率为( ).
A. B. C. D.
二、填空题(本大题共4小题,每小题4分,共16分.)
13.若由一个列联表中的数据计算得,那么有_______ _把握认为这两个变量有关系。
14.一同学在电脑中打出如下图若干个圆(○表示空心圆,●表示实心圆)
○●○○●○○○●○○○○●○○○○○●○……
问:到120个圆中有________ 个实心圆。
15完成下面的三段论:
大前提:互为共轭复数的乘积是实数
小前提:与是互为共轭复数
结 论:
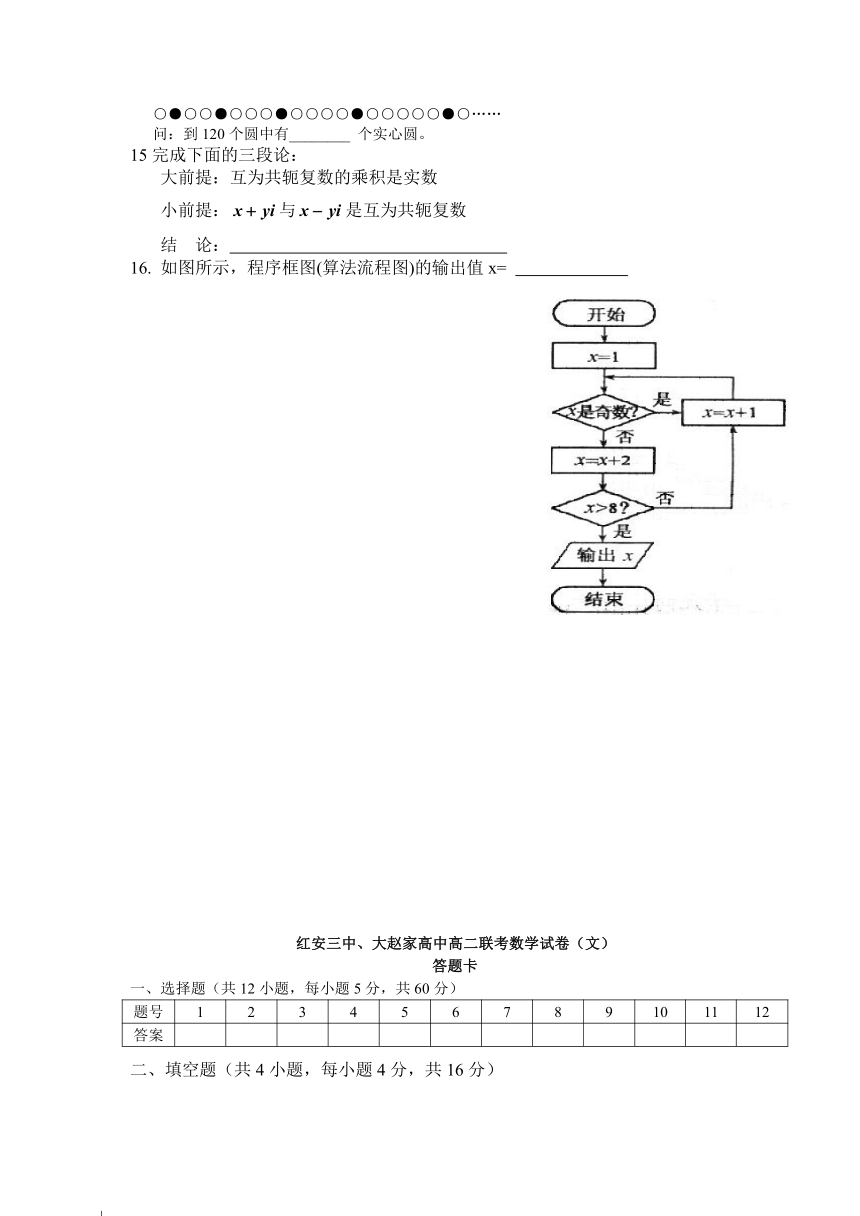
16. 如图所示,程序框图(算法流程图)的输出值x=
红安三中、大赵家高中高二联考数学试卷(文)
答题卡
一、选择题(共12小题,每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题(共4小题,每小题4分,共16分)
13 14
15 16
三、解答题(本大题共6小题,共74分.解答应在答题纸对应区域内写出必要的文字说明、证明过程或演算步骤.)
17.已知复数,,且为纯虚数,求复数.(12分)
18.(12分)已知,,。求证中至少有一个不小于0。
19.(本小题满分12分)
袋中有大小、形状相同的红、黑球各一个,现有放回地随机摸取3次,每次摸取一个球
(I)试问:一共有多少种不同的结果?请列出所有可能的结果;
(Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率。
20.在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
(1).证明:
(2). 求AE与D1F所成的角;(12分)
21.(本小题满分13分)
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
轿车A
轿车B
轿车C
舒适型
100
150
z
标准型
300
450
600
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
求z的值.
用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
22.(本小题满分13分)
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中个抽出500件,量其内径尺寸的结果如下表:
甲厂
分组
[29.86,29.90)
[29.90,29.94)
[29.94,29.98)
[29.98,30.02)
[30.02,30.06)
[30.06,30.10)
[30.10,30.14)
频数
12
63
86
182
92
61
4
乙厂
分组
[29.86,29.90)
[29.90,29.94)
[29.94,29.98)
[29.98,30.02)
[30.02,30.06)
[30.06,30.10)
[30.10,30.14)
频数
29
71
85
159
76
62
18
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由于以上统计数据填下面列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
甲 厂
乙 厂
合计
优质品
非优质品
合计
红安三中、大赵家高中高二联考数学试卷(文)
答案
一、选择题(共12小题,每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
B
D
C
B
A
C
D
C
C
A
二、填空题(共4小题,每小题4分,共16分)
13_____95%_______ 14___14_____
15是实数 16_____12____
三、解答题
17.解:略
18.证明:假设中没有一个不小于0,即, … 4分
所以 …6分
又 …10分
这与假设所得结论矛盾,故假设不成立 … 12分
所以中至少有一个不小于0
19.解:(I)一共有8种不同的结果,列举如下:
(红、红、红、)、(红、红、黑)、(红、黑、红)、(红、黑、黑)、(黑、红、红)、(黑、红、黑)、(黑、黑、红)、(黑、黑、黑) …… 6分
(Ⅱ)记“3次摸球所得总分为5”为事件A
事件A包含的基本事件为:(红、红、黑)、(红、黑、红)、(黑、红、红)事件A包含的基本事件数为3
由(I)可知,基本事件总数为8,所以事件A的概率为 . ………. 12分
20..证明:(1). 正方体ABCD-A1B1C1D1, ,,
………..6分
(2) 取AB的中点,并连接A1P, 易证, 可证;,
即,所以AE与D1F所成的角为 ………12分
21.解: (1).设该厂本月生产轿车为n辆,由题意得,,所以n=2000. z=2000-100-300-150-450-600=400 ……..4分
(2) 设所抽样本中有m辆舒适型轿车,因为用分层抽样的方法在C类轿车中抽取一个容量为5的样本,所以,解得m=2也就是抽取了2辆舒适型轿车,3辆标准型轿车,分别记作S1,S2;B1,B2,B3,则从中任取2辆的所有基本事件为(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),(B1 ,B2), (B2 ,B3) ,(B1 ,B3)共10个,其中至少有1辆舒适型轿车的基本事件有7个基本事件: (S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),所以从中任取2辆,至少有1辆舒适型轿车的概率为…..9分
(3)样本的平均数为,
那么与样本平均数之差的绝对值不超过0.5的数为9.4, 8.6, 9.2, 8.7, 9.3, 9.0这6个数,总的个数为8,所以该数与样本平均数之差的绝对值不超过0.5的概率为. ………13分
22.解:(Ⅰ)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件的优质品率估计为;
乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质品率估计为
……6分
(Ⅱ)
甲厂
乙厂
合计
优质品
360
320
680
非优质品
140
180
320
合计
500
500
1000
……9分
所以有99%的把握认为“两个分厂生产的零件的质量有差异”。 ……13分
参考公式:
用最小二乘法求线性回归方程系数公式
P(K2≥k0)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
一、选择题(本大题共12小题,每小题5分,共60分.在每小题的四个选项中,只有一项符合题目要求.)
1.复数的共轭复数是 ( )
A. B. C. D.
2.已知x与y之间的一组数据:
x
0
1
2
3
y
1
3
5
7
则y与x的线性回归方程为必过点 ( )
A .(2,2) B.(1,2) C.(1.5,0) D.(1.5,4)
3.用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是 ( )
A.假设三内角都不大于60度; B.假设三内角都大于60度;
C.假设三内角至多有一个大于60度; D.假设三内角至多有两个大于60度
4.下列表述正确的是 ( )
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理。
A.①②③ B.②③④ C.②④⑤ D.①③⑤
5.若 ( )
A. B. C.6 D.8
6.在复平面内,复数对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.在下列表格中,每格填上一个数字后,使每一行
成等差数列,每一列成等比数列,则a+b+c的值是( )
1
?
2
?
?
0.5
?
1
?
?
?
?
a
?
?
?
?
?
b
?
?
?
?
?
c
A. 1 B. 2
C. 3 D. 4
8.从装有除颜色外完全相同的2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的两个事件是( ).
A.至少有1个白球,都是白球 B.至少有1个白球,至少有1个红球
C.恰有1个白球,恰有2个白球 D.至少有1个白球,都是红球
9.现有五个球分别记为A,C,J,K,S,随机放进三个盒子,每个盒子只能放一个球,则K或S在盒中的概率是( )
A. B. C. D.
10.从{a,b,c,d,e}的所有子集中任取一个,这个集合恰是集合{a,b,c}的子集的概率是( )
A. B. C. D.
11. 给出下列命题
(1)实数的共轭复数一定是实数;
(2)复数与其共轭复数的差是纯虚数:
(3)若,则
其中正确命题的序号是( )
A B C D
12.在区间上随机取一个数x,的值介于0到之间的概率为( ).
A. B. C. D.
二、填空题(本大题共4小题,每小题4分,共16分.)
13.若由一个列联表中的数据计算得,那么有_______ _把握认为这两个变量有关系。
14.一同学在电脑中打出如下图若干个圆(○表示空心圆,●表示实心圆)
○●○○●○○○●○○○○●○○○○○●○……
问:到120个圆中有________ 个实心圆。
15完成下面的三段论:
大前提:互为共轭复数的乘积是实数
小前提:与是互为共轭复数
结 论:
16. 如图所示,程序框图(算法流程图)的输出值x=
红安三中、大赵家高中高二联考数学试卷(文)
答题卡
一、选择题(共12小题,每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题(共4小题,每小题4分,共16分)
13 14
15 16
三、解答题(本大题共6小题,共74分.解答应在答题纸对应区域内写出必要的文字说明、证明过程或演算步骤.)
17.已知复数,,且为纯虚数,求复数.(12分)
18.(12分)已知,,。求证中至少有一个不小于0。
19.(本小题满分12分)
袋中有大小、形状相同的红、黑球各一个,现有放回地随机摸取3次,每次摸取一个球
(I)试问:一共有多少种不同的结果?请列出所有可能的结果;
(Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率。
20.在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
(1).证明:
(2). 求AE与D1F所成的角;(12分)
21.(本小题满分13分)
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
轿车A
轿车B
轿车C
舒适型
100
150
z
标准型
300
450
600
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
求z的值.
用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
22.(本小题满分13分)
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中个抽出500件,量其内径尺寸的结果如下表:
甲厂
分组
[29.86,29.90)
[29.90,29.94)
[29.94,29.98)
[29.98,30.02)
[30.02,30.06)
[30.06,30.10)
[30.10,30.14)
频数
12
63
86
182
92
61
4
乙厂
分组
[29.86,29.90)
[29.90,29.94)
[29.94,29.98)
[29.98,30.02)
[30.02,30.06)
[30.06,30.10)
[30.10,30.14)
频数
29
71
85
159
76
62
18
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由于以上统计数据填下面列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
甲 厂
乙 厂
合计
优质品
非优质品
合计
红安三中、大赵家高中高二联考数学试卷(文)
答案
一、选择题(共12小题,每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
B
D
C
B
A
C
D
C
C
A
二、填空题(共4小题,每小题4分,共16分)
13_____95%_______ 14___14_____
15是实数 16_____12____
三、解答题
17.解:略
18.证明:假设中没有一个不小于0,即, … 4分
所以 …6分
又 …10分
这与假设所得结论矛盾,故假设不成立 … 12分
所以中至少有一个不小于0
19.解:(I)一共有8种不同的结果,列举如下:
(红、红、红、)、(红、红、黑)、(红、黑、红)、(红、黑、黑)、(黑、红、红)、(黑、红、黑)、(黑、黑、红)、(黑、黑、黑) …… 6分
(Ⅱ)记“3次摸球所得总分为5”为事件A
事件A包含的基本事件为:(红、红、黑)、(红、黑、红)、(黑、红、红)事件A包含的基本事件数为3
由(I)可知,基本事件总数为8,所以事件A的概率为 . ………. 12分
20..证明:(1). 正方体ABCD-A1B1C1D1, ,,
………..6分
(2) 取AB的中点,并连接A1P, 易证, 可证;,
即,所以AE与D1F所成的角为 ………12分
21.解: (1).设该厂本月生产轿车为n辆,由题意得,,所以n=2000. z=2000-100-300-150-450-600=400 ……..4分
(2) 设所抽样本中有m辆舒适型轿车,因为用分层抽样的方法在C类轿车中抽取一个容量为5的样本,所以,解得m=2也就是抽取了2辆舒适型轿车,3辆标准型轿车,分别记作S1,S2;B1,B2,B3,则从中任取2辆的所有基本事件为(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),(B1 ,B2), (B2 ,B3) ,(B1 ,B3)共10个,其中至少有1辆舒适型轿车的基本事件有7个基本事件: (S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),所以从中任取2辆,至少有1辆舒适型轿车的概率为…..9分
(3)样本的平均数为,
那么与样本平均数之差的绝对值不超过0.5的数为9.4, 8.6, 9.2, 8.7, 9.3, 9.0这6个数,总的个数为8,所以该数与样本平均数之差的绝对值不超过0.5的概率为. ………13分
22.解:(Ⅰ)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件的优质品率估计为;
乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质品率估计为
……6分
(Ⅱ)
甲厂
乙厂
合计
优质品
360
320
680
非优质品
140
180
320
合计
500
500
1000
……9分
所以有99%的把握认为“两个分厂生产的零件的质量有差异”。 ……13分
