2.3.1 把握变量之间的依赖关系
图片预览



文档简介
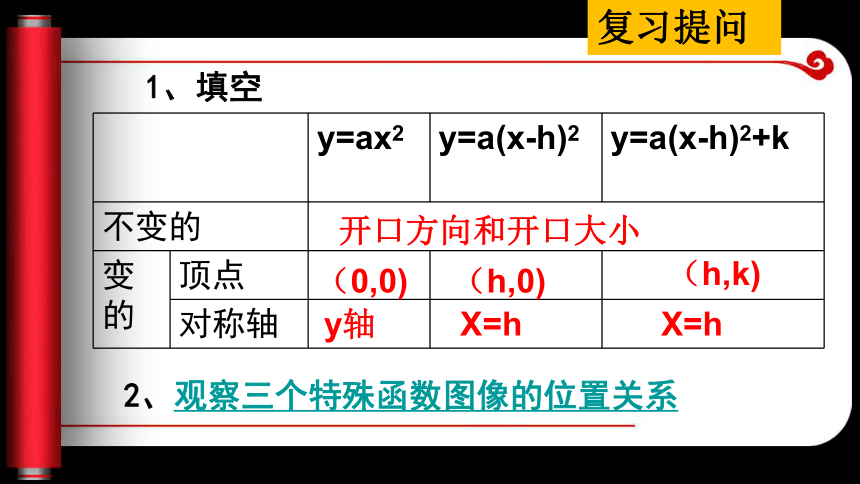
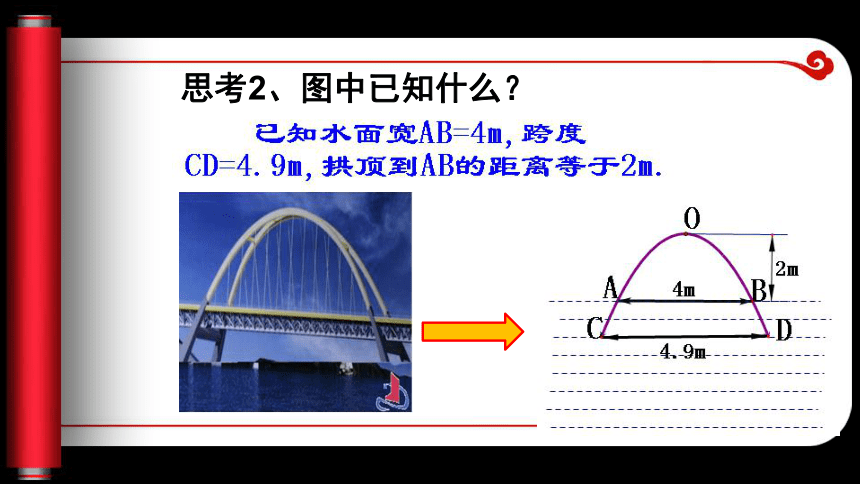
课件22张PPT。湖南省新邵县酿溪中学王军旗复习提问开口方向和开口大小(0,0)(h,0)(h,k)y轴X=hX=h1、填空2、观察三个特殊函数图像的位置关系 一座拱桥的纵截面是抛物线的一段,拱桥的跨度是4.9m,水面宽4m时,拱顶离水面2m,如图,当水面宽度发生变化时,拱顶离水面的高度会发生变化吗?会是怎样的变化?
你能想出办法来吗?动脑筋 这是二次函数的图像,因为它是抛物线的一段。思考1、这是什么函数图像?为什么?
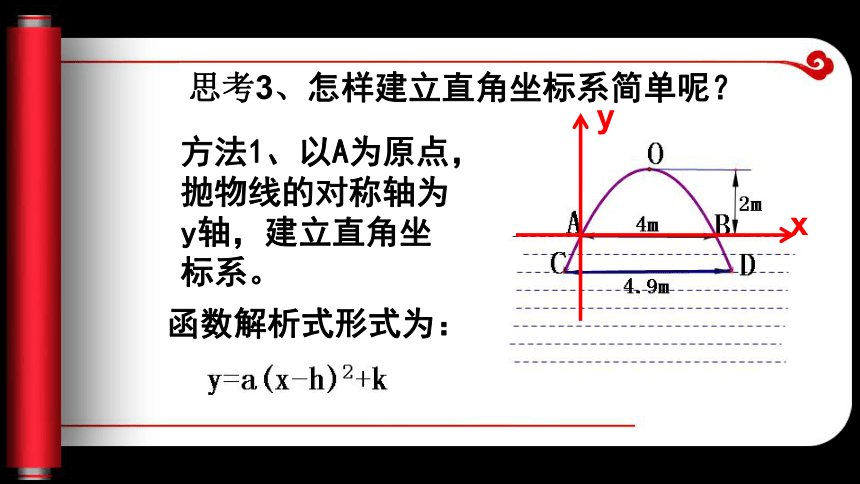
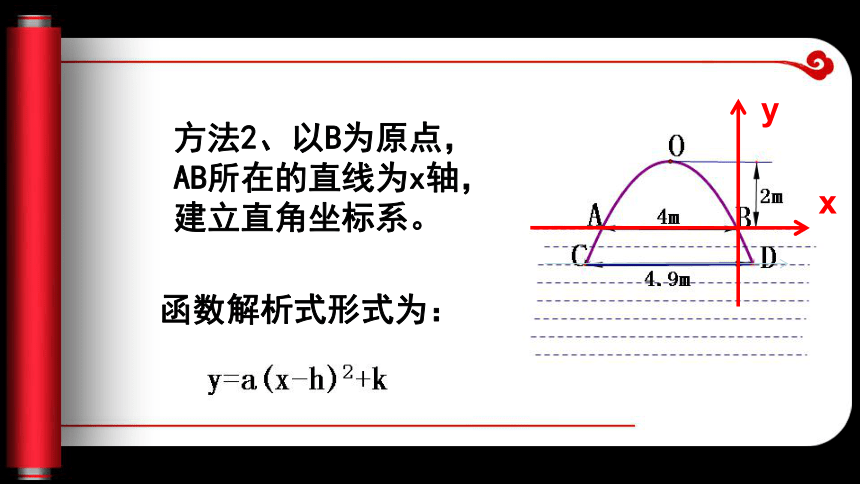
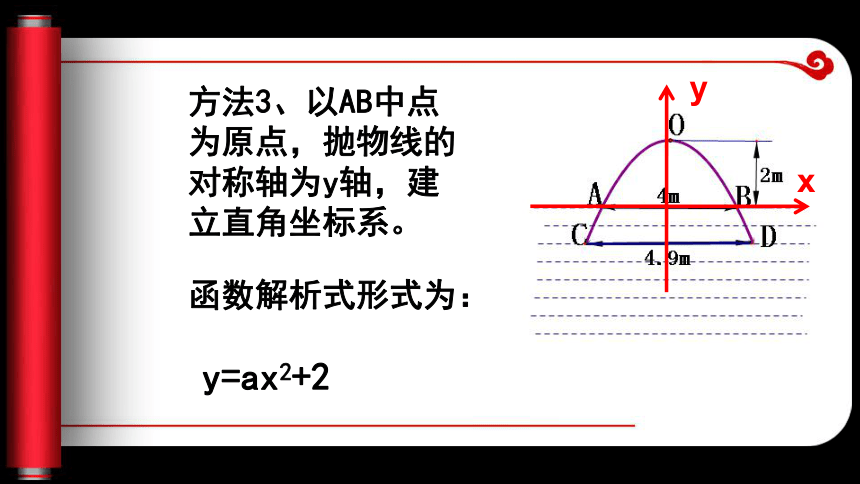
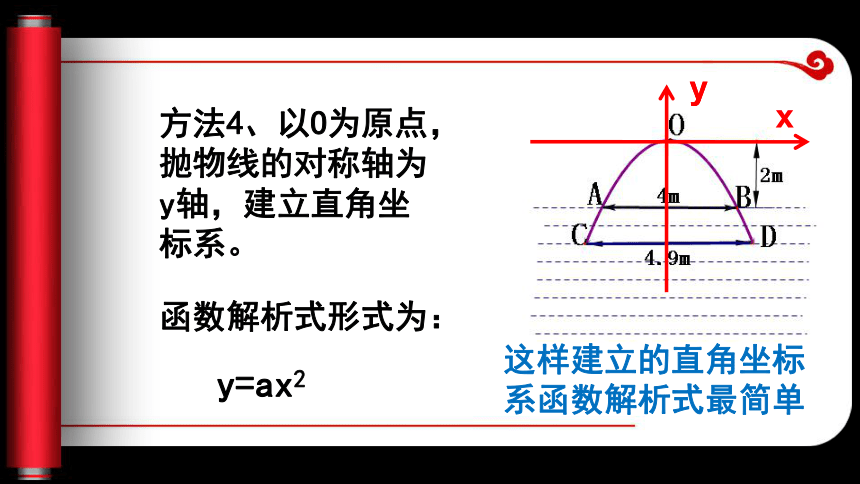
思考2、图中已知什么?思考3、怎样建立直角坐标系简单呢?方法1、以A为原点,抛物线的对称轴为y轴,建立直角坐标系。xy函数解析式形式为:方法2、以B为原点,AB所在的直线为x轴,建立直角坐标系。xy函数解析式形式为:方法3、以AB中点为原点,抛物线的对称轴为y轴,建立直角坐标系。y=ax2+2函数解析式形式为:xy方法4、以O为原点,抛物线的对称轴为y轴,建立直角坐标系。y=ax2xyy函数解析式形式为:这样建立的直角坐标系函数解析式最简单思考4、若设数轴上一个单位代表1m怎样求这个函数的解析式?【分析】关键是知道图像上一个点的坐标,将这个点的坐标代入解析式: y=ax2∵ B(2,-2)在抛物线上,
∴ 22a=-2, ∴a=-0.5∴抛物线的解析式为y=-0.5 x2 思考5、这个函数中x表示什么实际意义?y表示什么实际意义? 表示水面宽度一半。 表示水面与拱顶的距离。思考6、自变量的取值范围是什么?由于桥的跨度是4.9m,所以自变量的取值范围是:-2.45解:当x=1.5时,
y=- 0.5×1.52=-1.125
∴水面宽为3m时,拱顶离水面的高度为1.125m.E 用抛物线的知识解决生活中的一些实际问题的一般步骤:弄清题中量与量之间的依赖关系 建立函数模型利用二次函数图像和性质解决实际问题注意自变量的取值范围 【例1】某厂生产两种产品,价格分别为p1=4万元/吨、p2=8万元/吨。第一种产品的产量为Q1吨,第二种产品的产量为1吨,成本函数为:C=Q12+2Q1+5 (1)当Q1=1吨时,成本C是多少? (2)求利润L与Q1的函数关系式。 (3)当Q1=0.8吨时,利润L是多少?(4)当Q1等于多少时,利润L最大? 【例1】某厂生产两种产品,价格分别为p1=4万元/吨、p2=8万元/吨。第一种产品的产量为Q1吨,第二种产品的产量为1吨,成本函数为:C=Q12+2Q1+5 (1)当Q1=1吨时,成本C是多少?解:(1)当Q1=1吨时,c=12+2×1+5=8(万元)【例1】某厂生产两种产品,价格分别为p1=4万元/吨、p2=8万元/吨。第一种产品的产量为Q1吨,第二种产品的产量为1吨,成本函数为:C=Q12+2Q1+5 (2)求利润L与Q1的函数关系式。解:(2)L=售价-成本=(第一种产品的售价+第二种产品的售价)-成本
∴ L=4 Q1+1×8-(Q12+2Q1+5)=-Q12+2Q1+3解:当Q1=0.8时,
L=-0.82+2×0.8+3=3.06【例1】某厂生产两种产品,价格分别为p1=4万元/吨、p2=8万元/吨。第一种产品的产量为Q1吨,第二种产品的产量为1吨,成本函数为:C=Q12+2Q1+5 (3)当Q1=0.8吨时,利润L是多少?解:(4)L=-(Q12-2Q1)+3
=-( Q12-2Q1+1-1)+3=-(Q1-1)2+4
∴当 Q1=1吨时,利润最大,最大值为4万元。 【例1】某厂生产两种产品,价格分别为p1=4万元/吨、p2=8万元/吨。第一种产品的产量为Q1吨,第二种产品的产量为1吨,成本函数为:C=Q12+2Q1+5 (4)当Q1等于多少时,利润L最大? 一条隧道顶部的纵截面是抛物线形,拱高2.5m,跨度为10m,如图,试建立适当的直角坐标系,求出二次函数,使的图像的一段为拱形抛物线。解:如图建立直角坐标系,
设抛物线解析式为: y=ax2
点A(5,-2.5)在抛物线上
∴-2.5=a×52,a=-0.1
练习:XyA∴y=-0.1x 2 小结
用抛物线的知识解决生活中的一些实际问题的一般步骤是,先弄清题中量与量之间的依赖关系,然后建立函数模型,再利用二次函数图像和性质解决实际问题,但要注意自变量的取值范围。
作业:P 49 1,2,3
思考2、图中已知什么?思考3、怎样建立直角坐标系简单呢?方法1、以A为原点,抛物线的对称轴为y轴,建立直角坐标系。xy函数解析式形式为:方法2、以B为原点,AB所在的直线为x轴,建立直角坐标系。xy函数解析式形式为:方法3、以AB中点为原点,抛物线的对称轴为y轴,建立直角坐标系。y=ax2+2函数解析式形式为:xy方法4、以O为原点,抛物线的对称轴为y轴,建立直角坐标系。y=ax2xyy函数解析式形式为:这样建立的直角坐标系函数解析式最简单思考4、若设数轴上一个单位代表1m怎样求这个函数的解析式?【分析】关键是知道图像上一个点的坐标,将这个点的坐标代入解析式: y=ax2∵ B(2,-2)在抛物线上,
∴ 22a=-2, ∴a=-0.5∴抛物线的解析式为y=-0.5 x2 思考5、这个函数中x表示什么实际意义?y表示什么实际意义? 表示水面宽度一半。 表示水面与拱顶的距离。思考6、自变量的取值范围是什么?由于桥的跨度是4.9m,所以自变量的取值范围是:-2.45
y=- 0.5×1.52=-1.125
∴水面宽为3m时,拱顶离水面的高度为1.125m.E 用抛物线的知识解决生活中的一些实际问题的一般步骤:弄清题中量与量之间的依赖关系 建立函数模型利用二次函数图像和性质解决实际问题注意自变量的取值范围 【例1】某厂生产两种产品,价格分别为p1=4万元/吨、p2=8万元/吨。第一种产品的产量为Q1吨,第二种产品的产量为1吨,成本函数为:C=Q12+2Q1+5 (1)当Q1=1吨时,成本C是多少? (2)求利润L与Q1的函数关系式。 (3)当Q1=0.8吨时,利润L是多少?(4)当Q1等于多少时,利润L最大? 【例1】某厂生产两种产品,价格分别为p1=4万元/吨、p2=8万元/吨。第一种产品的产量为Q1吨,第二种产品的产量为1吨,成本函数为:C=Q12+2Q1+5 (1)当Q1=1吨时,成本C是多少?解:(1)当Q1=1吨时,c=12+2×1+5=8(万元)【例1】某厂生产两种产品,价格分别为p1=4万元/吨、p2=8万元/吨。第一种产品的产量为Q1吨,第二种产品的产量为1吨,成本函数为:C=Q12+2Q1+5 (2)求利润L与Q1的函数关系式。解:(2)L=售价-成本=(第一种产品的售价+第二种产品的售价)-成本
∴ L=4 Q1+1×8-(Q12+2Q1+5)=-Q12+2Q1+3解:当Q1=0.8时,
L=-0.82+2×0.8+3=3.06【例1】某厂生产两种产品,价格分别为p1=4万元/吨、p2=8万元/吨。第一种产品的产量为Q1吨,第二种产品的产量为1吨,成本函数为:C=Q12+2Q1+5 (3)当Q1=0.8吨时,利润L是多少?解:(4)L=-(Q12-2Q1)+3
=-( Q12-2Q1+1-1)+3=-(Q1-1)2+4
∴当 Q1=1吨时,利润最大,最大值为4万元。 【例1】某厂生产两种产品,价格分别为p1=4万元/吨、p2=8万元/吨。第一种产品的产量为Q1吨,第二种产品的产量为1吨,成本函数为:C=Q12+2Q1+5 (4)当Q1等于多少时,利润L最大? 一条隧道顶部的纵截面是抛物线形,拱高2.5m,跨度为10m,如图,试建立适当的直角坐标系,求出二次函数,使的图像的一段为拱形抛物线。解:如图建立直角坐标系,
设抛物线解析式为: y=ax2
点A(5,-2.5)在抛物线上
∴-2.5=a×52,a=-0.1
练习:XyA∴y=-0.1x 2 小结
用抛物线的知识解决生活中的一些实际问题的一般步骤是,先弄清题中量与量之间的依赖关系,然后建立函数模型,再利用二次函数图像和性质解决实际问题,但要注意自变量的取值范围。
作业:P 49 1,2,3
