向量的减法
图片预览





文档简介
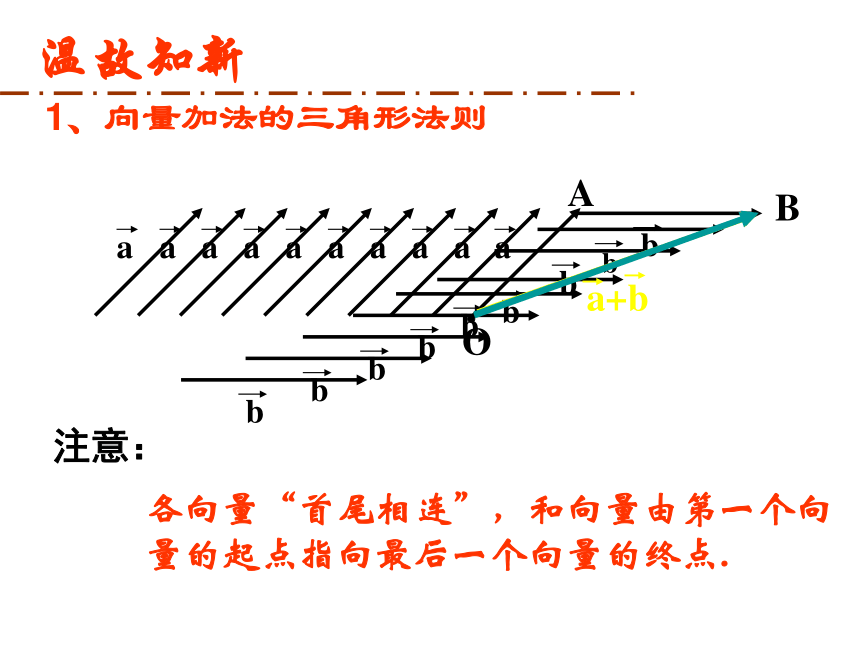
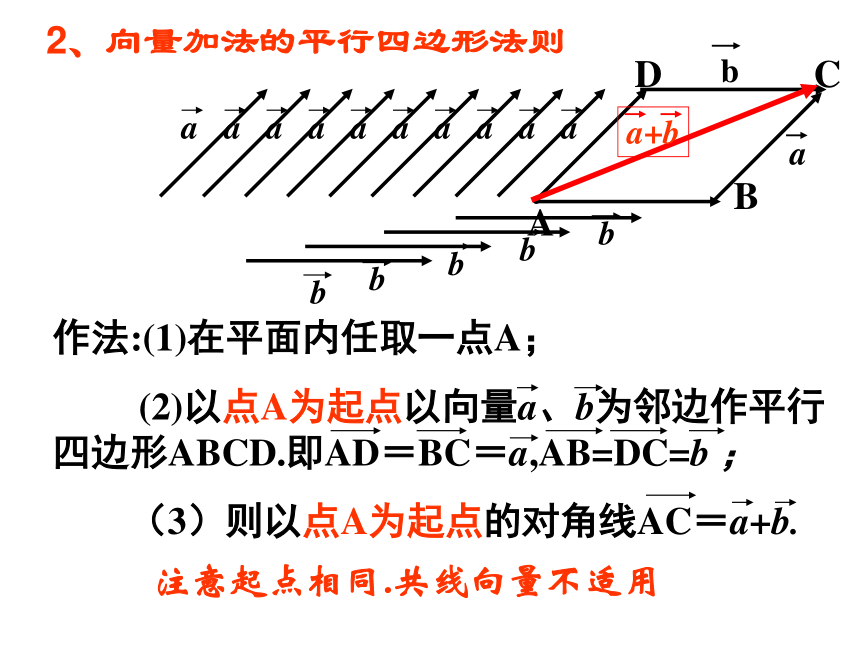
课件25张PPT。 高中数学必修 4国际育才高一数学组2019年3月10日星期日向量减法运算及其几何意义1、向量加法的三角形法则注意:各向量“首尾相连”,和向量由第一个向量的起点指向最后一个向量的终点.温故知新2、向量加法的平行四边形法则注意起点相同.共线向量不适用
走进新课如何理解定义向量的减法呢?数的减法定义即减去一个数等于加上这个数的相反数,如:5-1=5+(-1),因此定义数的减法运算,必须先引入一个相反数的概念.
类似的,请同学们思考:
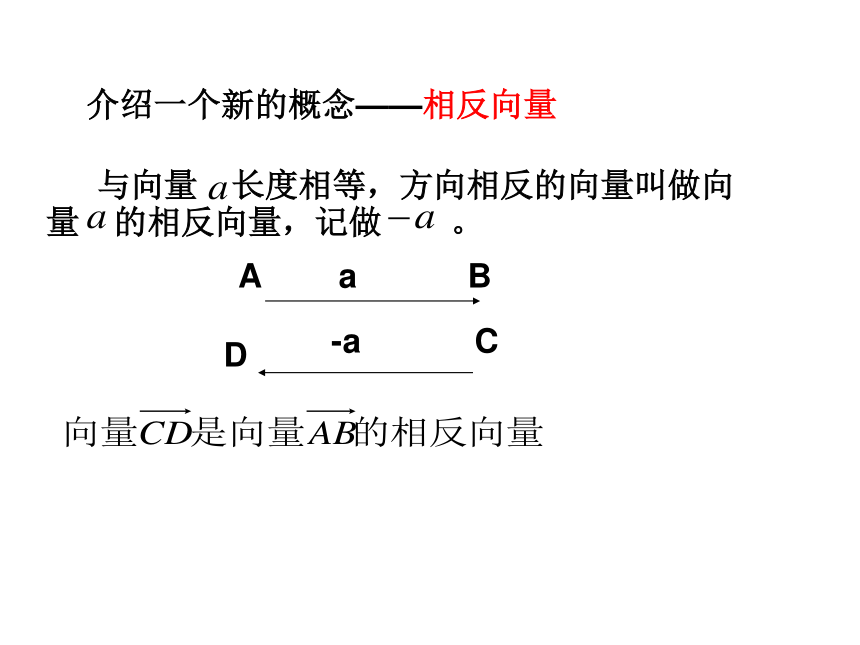
类比数的 减法运算,我们定义向量的减法运算,也应引进一个新的概念,这个概念又如何定义呢? 与向量 长度相等,方向相反的向量叫做向量 的相反向量,记做 。介绍一个新的概念——相反向量练习说明:
1、 与 互为相反向量
2、零向量的相反向量仍是零向量
3、任一向量和它相反向量的和是零向量由此,我们得到:
减去一个向量等于加上这个向量的相反向量CD二、向量减法的三角形法则OAB. 注意:
1、两个向量相减,则表示两个向量起点的字母必须相同
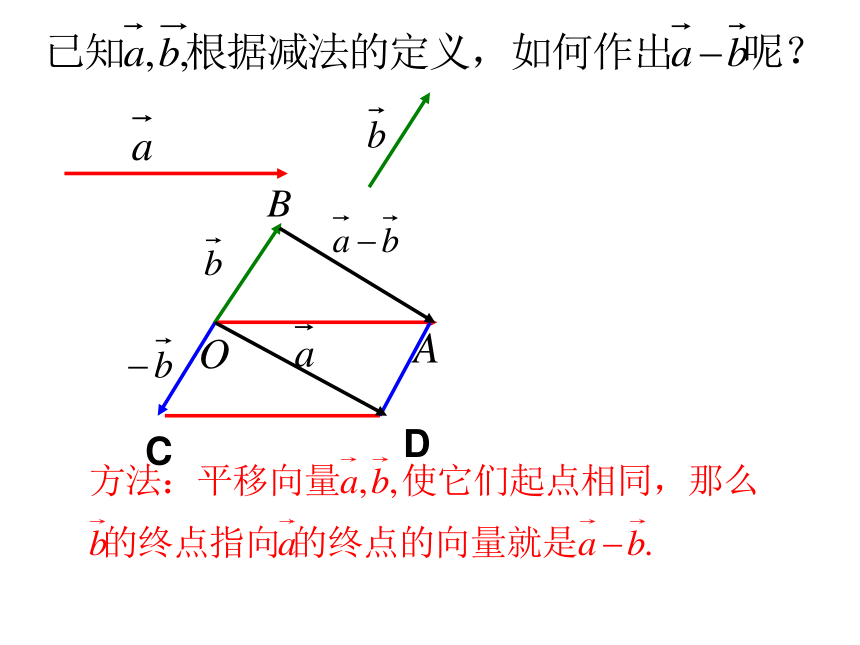
2、差向量的终点指向被减向量的终点向量减法的几何意义:可以表示为从向量 的
终点指向向量 的终点的向量.练习?特殊情况:若 ,怎样做出1.共线同向2.共线反向C例1:如图,已知向量a,b,c,d,
求作向量a-b,c-d.abcdOABCD例2:如图,平行四边形ABCD,AB=a,AD=b,用a、b表示向量AC、DB。ADBCab练习
(1)(2)(3)(4)练习
(1)(2)(3)(4)不可能.因为平行四边形的两条对角线方向不同.变式训练四:变式训练五 30° (一)知识
1.理解相反向量的概念
2. 理解向量减法的定义及其几何意义
3. 正确熟练地掌握向量减法的三角形法则:
1)共起点
2)连终点
3)方向指向被减向量的终点
小结:
(二)方法
类比,数形结合,
几何作图,分类讨论等思想方法练习
走进新课如何理解定义向量的减法呢?数的减法定义即减去一个数等于加上这个数的相反数,如:5-1=5+(-1),因此定义数的减法运算,必须先引入一个相反数的概念.
类似的,请同学们思考:
类比数的 减法运算,我们定义向量的减法运算,也应引进一个新的概念,这个概念又如何定义呢? 与向量 长度相等,方向相反的向量叫做向量 的相反向量,记做 。介绍一个新的概念——相反向量练习说明:
1、 与 互为相反向量
2、零向量的相反向量仍是零向量
3、任一向量和它相反向量的和是零向量由此,我们得到:
减去一个向量等于加上这个向量的相反向量CD二、向量减法的三角形法则OAB. 注意:
1、两个向量相减,则表示两个向量起点的字母必须相同
2、差向量的终点指向被减向量的终点向量减法的几何意义:可以表示为从向量 的
终点指向向量 的终点的向量.练习?特殊情况:若 ,怎样做出1.共线同向2.共线反向C例1:如图,已知向量a,b,c,d,
求作向量a-b,c-d.abcdOABCD例2:如图,平行四边形ABCD,AB=a,AD=b,用a、b表示向量AC、DB。ADBCab练习
(1)(2)(3)(4)练习
(1)(2)(3)(4)不可能.因为平行四边形的两条对角线方向不同.变式训练四:变式训练五 30° (一)知识
1.理解相反向量的概念
2. 理解向量减法的定义及其几何意义
3. 正确熟练地掌握向量减法的三角形法则:
1)共起点
2)连终点
3)方向指向被减向量的终点
小结:
(二)方法
类比,数形结合,
几何作图,分类讨论等思想方法练习
