二次函数y=a(x-h)2的图像和性质
文档属性
| 名称 | 二次函数y=a(x-h)2的图像和性质 |

|
|
| 格式 | rar | ||
| 文件大小 | 44.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-12-19 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
课题:二次函数y=a(x-h)2的图像和性质
学习目标 1、知道二次函数y=a(x-h)2(a≠0)与y=ax2(a≠0)图象之间的关系;2、能说出二次函数y=a(x-h)2(a≠0)的开口方向、对称轴和顶点坐标,理解其增减性;3、学习利用“从特殊到一般”的方法研究问题
重点难点 重点: y=a(x-h)2(a≠0)类型函数的图像特点及性质。难点:灵活运用 y=a(x-h)2(a≠0)类型函数的性质解决问题。
教学过程 修订
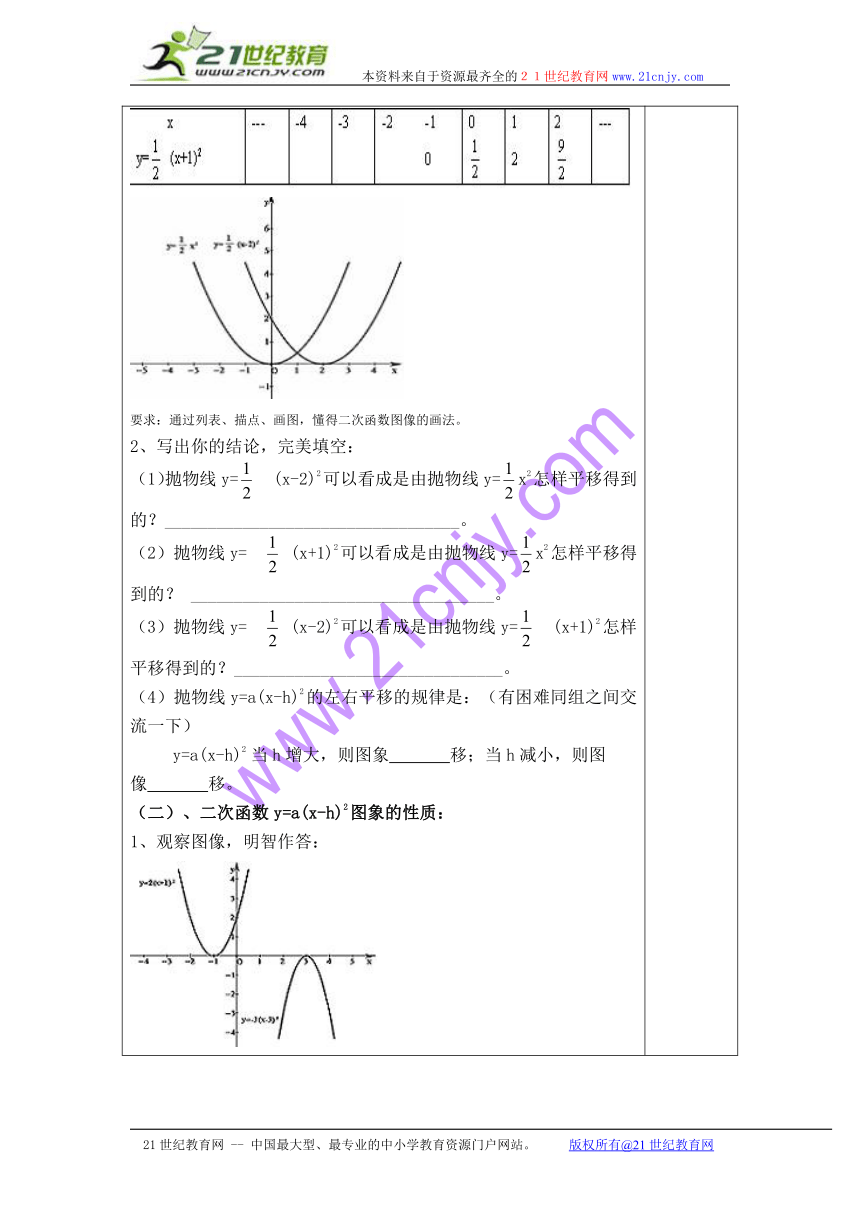
一、温故互查(二人小组完成)1、抛物线y=2x2怎样平移得到抛物线y=2x2-2的?_______________________________________2、抛物线y=2x2-2怎样平移得到抛物线y=2x2+3的? _______________________________________3、y=ax2+k的图象平移规律是:上、下平移改变____值,具体是___________。4、抛物线y= - 4x2的开口方向是__________,对称轴是________,顶点坐标是( )。5、抛物线y=x2-3的开口方向是________,对称轴是____________,顶点坐标是( ),当x_______时,y最____值=_______,当x_______时,y随x的增大而增大,当x_______时,y随x的增大而减小。二、合作探究(四人小组完成)(一)、探究二次函数y=a(x-h)2图象左右平移的规律要求:全体学生完成,小组展示成果。1、图中的坐标系中已画出了二次函数y=x2和y= (x-2)2的图象,请在下面的坐标系中,再画出y= (x+1)2的图象
教学过程 修订
要求:通过列表、描点、画图,懂得二次函数图像的画法。2、写出你的结论,完美填空:(1)抛物线y= (x-2)2可以看成是由抛物线y=x2怎样平移得到的?__________________________________。(2)抛物线y= (x+1)2可以看成是由抛物线y=x2怎样平移得到的? ___________________________________。(3)抛物线y= (x-2)2可以看成是由抛物线y= (x+1)2怎样平移得到的?_______________________________。(4)抛物线y=a(x-h)2的左右平移的规律是:(有困难同组之间交流一下)y=a(x-h)2 当h增大,则图象 移;当h减小,则图像 移。(二)、二次函数y=a(x-h)2图象的性质:1、观察图像,明智作答:
教学过程 修订
(1)、抛物线y=2 (x+1)2 的开口方向是______,顶点坐标( ),对称轴是_____________________,当x_______时,y最____值=_______,当x_______时,y随x的增大而增大,当x_______时,y随x的增大而减小。(2)、抛物线y= -3(x-3)2 的开口方向是______,顶点坐标( ),对称轴是_____________________,当x_______时,y最____值=_______,当x_______时,y随x的增大而增大,当x_______时,y随x的增大而减小。根据刚才的学习,总结一下:y=a(x-h)2(a≠0)开口方向对称轴顶点标增减性a﹥0a﹤0自学检测:要求:在各自独立完成的基础上,以小组为单位进行检查,做得既快又好的同学指导本组学习有困难的同学。将抛物线y= -3x2向右平移1个单位,则所得抛物线的关系式为_________________,平移之后的抛物线的开口__________,对称轴是_____________,顶点坐标是_____________,当x_______时,y最_________值=___________,当x_________时,y随x的增大而增大,当x__________时,y随x的增大而减小。2、将抛物线y= x2+1向右平移2个单位,所得抛物线是________.3、抛物线y= x2先向左平移1个单位,再向右平移4个单位,则平移后的抛物线的解析式为_______________________。4、已知抛物线y=ax2与抛物线y= -2 (x-h)2 的形状相同,且将抛物线y=ax2沿x轴向左平移2个单位,就能与抛物线y= -2 (x-h)2 完全重合,则a=_______,h=______。
教学过程 修订
四、巩固训练:要求:在小组合作完成的基础上,选派代表进行展示,并说明理由,其他小组做补充。1、已知一条抛物线的对称轴是直线x= -3,其开口大小和方向与抛物线y= 2x2的相同,若其顶点在x轴上,则该函数的解析式为___________________________。2、点A(2,y1)和点B(3,y2)是抛物线y= -(x - 1)2的两点,试比较y1,y2的大小。 3、抛物线y=(x-4)2与抛物线___________关于x轴对称;抛物线y=-(x-4)2与抛物线____________关于轴对称。五、拓展延伸:(学有余力的同学相互探究开发思维) 由于被墨水污染,一道数学题仅能见到如下文字:已知二次函数 y=a(x-h)2的图象过点(1,8),---根据现有信息,题中的二次函数图象不具有的性质是( )A、过点(3,0) B、过点(5,8) C、开口向下 D、在对称轴右侧y随x的增大而增大六、课堂小结:以小组为单位,相互交流本节课的收获和困惑,最后由组长收集整理并进行汇报总结。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
课题:二次函数y=a(x-h)2的图像和性质
学习目标 1、知道二次函数y=a(x-h)2(a≠0)与y=ax2(a≠0)图象之间的关系;2、能说出二次函数y=a(x-h)2(a≠0)的开口方向、对称轴和顶点坐标,理解其增减性;3、学习利用“从特殊到一般”的方法研究问题
重点难点 重点: y=a(x-h)2(a≠0)类型函数的图像特点及性质。难点:灵活运用 y=a(x-h)2(a≠0)类型函数的性质解决问题。
教学过程 修订
一、温故互查(二人小组完成)1、抛物线y=2x2怎样平移得到抛物线y=2x2-2的?_______________________________________2、抛物线y=2x2-2怎样平移得到抛物线y=2x2+3的? _______________________________________3、y=ax2+k的图象平移规律是:上、下平移改变____值,具体是___________。4、抛物线y= - 4x2的开口方向是__________,对称轴是________,顶点坐标是( )。5、抛物线y=x2-3的开口方向是________,对称轴是____________,顶点坐标是( ),当x_______时,y最____值=_______,当x_______时,y随x的增大而增大,当x_______时,y随x的增大而减小。二、合作探究(四人小组完成)(一)、探究二次函数y=a(x-h)2图象左右平移的规律要求:全体学生完成,小组展示成果。1、图中的坐标系中已画出了二次函数y=x2和y= (x-2)2的图象,请在下面的坐标系中,再画出y= (x+1)2的图象
教学过程 修订
要求:通过列表、描点、画图,懂得二次函数图像的画法。2、写出你的结论,完美填空:(1)抛物线y= (x-2)2可以看成是由抛物线y=x2怎样平移得到的?__________________________________。(2)抛物线y= (x+1)2可以看成是由抛物线y=x2怎样平移得到的? ___________________________________。(3)抛物线y= (x-2)2可以看成是由抛物线y= (x+1)2怎样平移得到的?_______________________________。(4)抛物线y=a(x-h)2的左右平移的规律是:(有困难同组之间交流一下)y=a(x-h)2 当h增大,则图象 移;当h减小,则图像 移。(二)、二次函数y=a(x-h)2图象的性质:1、观察图像,明智作答:
教学过程 修订
(1)、抛物线y=2 (x+1)2 的开口方向是______,顶点坐标( ),对称轴是_____________________,当x_______时,y最____值=_______,当x_______时,y随x的增大而增大,当x_______时,y随x的增大而减小。(2)、抛物线y= -3(x-3)2 的开口方向是______,顶点坐标( ),对称轴是_____________________,当x_______时,y最____值=_______,当x_______时,y随x的增大而增大,当x_______时,y随x的增大而减小。根据刚才的学习,总结一下:y=a(x-h)2(a≠0)开口方向对称轴顶点标增减性a﹥0a﹤0自学检测:要求:在各自独立完成的基础上,以小组为单位进行检查,做得既快又好的同学指导本组学习有困难的同学。将抛物线y= -3x2向右平移1个单位,则所得抛物线的关系式为_________________,平移之后的抛物线的开口__________,对称轴是_____________,顶点坐标是_____________,当x_______时,y最_________值=___________,当x_________时,y随x的增大而增大,当x__________时,y随x的增大而减小。2、将抛物线y= x2+1向右平移2个单位,所得抛物线是________.3、抛物线y= x2先向左平移1个单位,再向右平移4个单位,则平移后的抛物线的解析式为_______________________。4、已知抛物线y=ax2与抛物线y= -2 (x-h)2 的形状相同,且将抛物线y=ax2沿x轴向左平移2个单位,就能与抛物线y= -2 (x-h)2 完全重合,则a=_______,h=______。
教学过程 修订
四、巩固训练:要求:在小组合作完成的基础上,选派代表进行展示,并说明理由,其他小组做补充。1、已知一条抛物线的对称轴是直线x= -3,其开口大小和方向与抛物线y= 2x2的相同,若其顶点在x轴上,则该函数的解析式为___________________________。2、点A(2,y1)和点B(3,y2)是抛物线y= -(x - 1)2的两点,试比较y1,y2的大小。 3、抛物线y=(x-4)2与抛物线___________关于x轴对称;抛物线y=-(x-4)2与抛物线____________关于轴对称。五、拓展延伸:(学有余力的同学相互探究开发思维) 由于被墨水污染,一道数学题仅能见到如下文字:已知二次函数 y=a(x-h)2的图象过点(1,8),---根据现有信息,题中的二次函数图象不具有的性质是( )A、过点(3,0) B、过点(5,8) C、开口向下 D、在对称轴右侧y随x的增大而增大六、课堂小结:以小组为单位,相互交流本节课的收获和困惑,最后由组长收集整理并进行汇报总结。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
