北师版九下二次函数与一元二次方程第1课时
文档属性
| 名称 | 北师版九下二次函数与一元二次方程第1课时 |  | |
| 格式 | rar | ||
| 文件大小 | 129.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-12-19 20:30:00 | ||
图片预览



文档简介
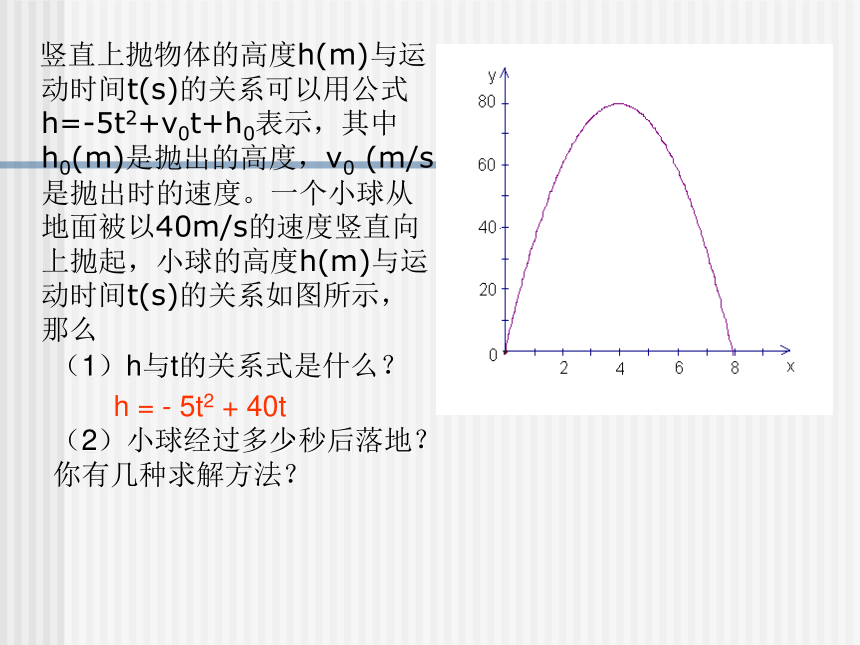
课件12张PPT。二次函数与一元二次方程第一课时 竖直上抛物体的高度h(m)与运动时间t(s)的关系可以用公式h=-5t2+v0t+h0表示,其中h0(m)是抛出的高度,v0 (m/s)是抛出时的速度。一个小球从地面被以40m/s的速度竖直向上抛起,小球的高度h(m)与运动时间t(s)的关系如图所示,那么
(1)h与t的关系式是什么?(2)小球经过多少秒后落地?你有几种求解方法?
h = - 5t2 + 40t议一议
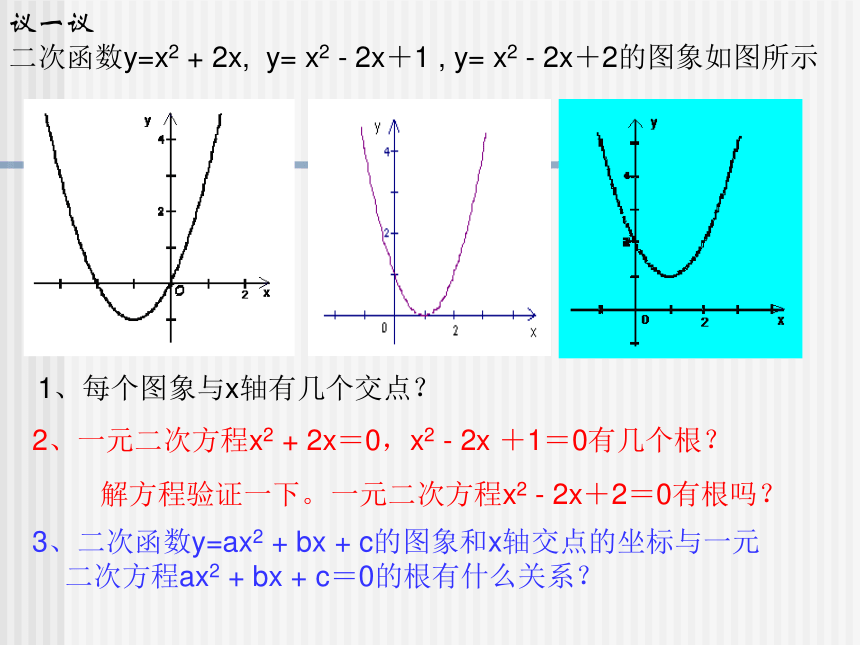
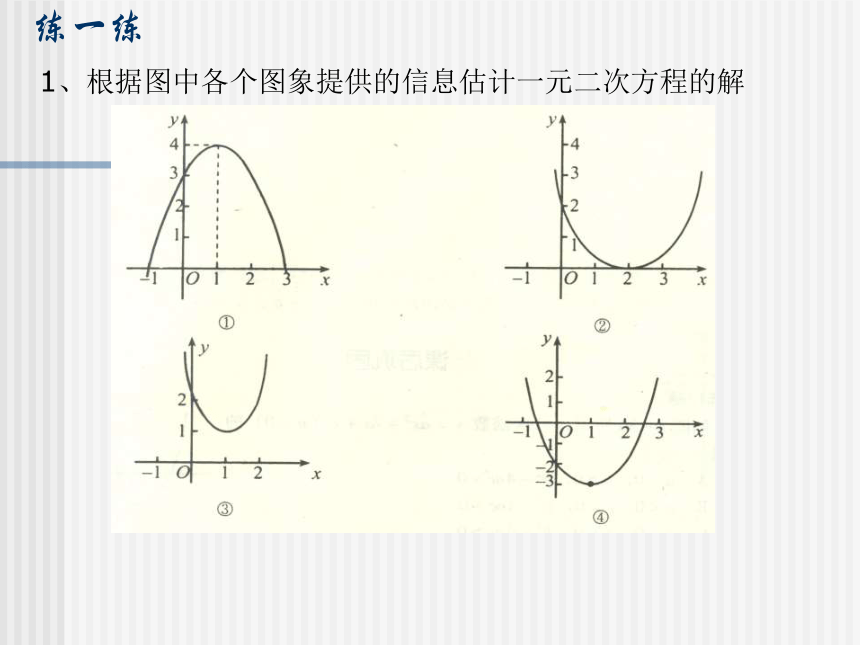
二次函数y=x2 + 2x, y= x2 - 2x+1 , y= x2 - 2x+2的图象如图所示1、每个图象与x轴有几个交点?2、一元二次方程x2 + 2x=0,x2 - 2x +1=0有几个根?3、二次函数y=ax2 + bx + c的图象和x轴交点的坐标与一元二次方程ax2 + bx + c=0的根有什么关系?解方程验证一下。一元二次方程x2 - 2x+2=0有根吗?二次函数y=ax2 + bx + c的图象与x轴的交点有三种情况:有两个交点、一个交点、没有交点。当二次函数y=ax2 + bx + c的图象与x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2 + bx + c=0的根。练一练1、根据图中各个图象提供的信息估计一元二次方程的解2、若二次函数与x轴交于A、B两点,求A、B两点的坐标及AB间的距离:
(1) y=x2 - 2x – 8
(2) y=3x2 + 2x – 1
(3) y= x2 - x + 0.253、竖直上抛物体的高度h(m)与运动时间t(s)的关系可以用公式h=-5t2+v0t+h0表示,其中h0(m)是抛出的高度,v0 (m/s)是抛出时的速度。一个小球从地面被以40m/s的速度竖直向上抛起,小球的高度h(m)与运动时间t(s)的关系如图所示,那么
h = - 5t2 + 40t何时小球离地面的高度是60?你是如何知道的?一个足球从地面向上踢出,它距地面的高度h(m)可以用公式 h = - 4.9t2 + 19.6t 来表示,其中t(s)表示足球被踢出后经过的时间。1、当t=1,t=2时,足球距地面的高度分别是多少?2、方程- 4.9t2 + 19.6t = 0、 - 4.9t2 + 19.6t = 14.7的根的实际意义分别是什么?横(2)方程x2-2x-3=-4的根,就是函数y=x2-2x-3的图象与直线y= 的交点的 坐标(1)方程x2-2x-3=0的根,就是函数y=x2-2x-3的图象与直线y=0的交点的 坐标
-4横例1:二次函数依次为A、B,与y轴交于点C,求A、B、C三点的坐标.的图象与x轴从左到右两个交点两根式例2:已知一个二次函数的图象过点(-1, 0)、
(3,0)、(0,-3)三点,求这个函数的解析式?小结1、二次函数y=ax2 + bx + c的图象与x轴的交点的横坐标就是一元二次方程ax2 + bx + c=0的根。
一元二次方程ax2 + bx + c=m的根,就是
二次函数y=ax2 + bx + c的图象与直线y=m的交点的横坐标在函数问题中,往往需要解方程:反过来也可以利用函数图象解方程。 2、二次函数的图象经过点A(x1,0),B(x2,0)则:y=a(x-x1)(x-x2)
(1)h与t的关系式是什么?(2)小球经过多少秒后落地?你有几种求解方法?
h = - 5t2 + 40t议一议
二次函数y=x2 + 2x, y= x2 - 2x+1 , y= x2 - 2x+2的图象如图所示1、每个图象与x轴有几个交点?2、一元二次方程x2 + 2x=0,x2 - 2x +1=0有几个根?3、二次函数y=ax2 + bx + c的图象和x轴交点的坐标与一元二次方程ax2 + bx + c=0的根有什么关系?解方程验证一下。一元二次方程x2 - 2x+2=0有根吗?二次函数y=ax2 + bx + c的图象与x轴的交点有三种情况:有两个交点、一个交点、没有交点。当二次函数y=ax2 + bx + c的图象与x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2 + bx + c=0的根。练一练1、根据图中各个图象提供的信息估计一元二次方程的解2、若二次函数与x轴交于A、B两点,求A、B两点的坐标及AB间的距离:
(1) y=x2 - 2x – 8
(2) y=3x2 + 2x – 1
(3) y= x2 - x + 0.253、竖直上抛物体的高度h(m)与运动时间t(s)的关系可以用公式h=-5t2+v0t+h0表示,其中h0(m)是抛出的高度,v0 (m/s)是抛出时的速度。一个小球从地面被以40m/s的速度竖直向上抛起,小球的高度h(m)与运动时间t(s)的关系如图所示,那么
h = - 5t2 + 40t何时小球离地面的高度是60?你是如何知道的?一个足球从地面向上踢出,它距地面的高度h(m)可以用公式 h = - 4.9t2 + 19.6t 来表示,其中t(s)表示足球被踢出后经过的时间。1、当t=1,t=2时,足球距地面的高度分别是多少?2、方程- 4.9t2 + 19.6t = 0、 - 4.9t2 + 19.6t = 14.7的根的实际意义分别是什么?横(2)方程x2-2x-3=-4的根,就是函数y=x2-2x-3的图象与直线y= 的交点的 坐标(1)方程x2-2x-3=0的根,就是函数y=x2-2x-3的图象与直线y=0的交点的 坐标
-4横例1:二次函数依次为A、B,与y轴交于点C,求A、B、C三点的坐标.的图象与x轴从左到右两个交点两根式例2:已知一个二次函数的图象过点(-1, 0)、
(3,0)、(0,-3)三点,求这个函数的解析式?小结1、二次函数y=ax2 + bx + c的图象与x轴的交点的横坐标就是一元二次方程ax2 + bx + c=0的根。
一元二次方程ax2 + bx + c=m的根,就是
二次函数y=ax2 + bx + c的图象与直线y=m的交点的横坐标在函数问题中,往往需要解方程:反过来也可以利用函数图象解方程。 2、二次函数的图象经过点A(x1,0),B(x2,0)则:y=a(x-x1)(x-x2)
