梯形的性质
图片预览
文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
课题:梯形的性质
课型:新授课 选自:华师大版八年级上册
教师 郝淑红 工作单位 武乡二中 科目 数学
学习目标 1. 探索并掌握梯形的有关概念、性质,了解常见的特殊梯形。2. 了解梯形中常用的作辅助线的方法,能将梯形分为平行四边形和三角形的转化方法解决一些简单问题。3. 经历探索梯形性质的过程,进一步培养分析问题能力和计算能力。
重点难点 重点:1.探索并理解记忆梯形、等腰梯形、直角梯形的有关性质。2.理解梯形的性质,发展合情推理能力。难点:1.等腰梯形性质的记忆与正确运用。2.学会几何语言表达。
教学活动 修订
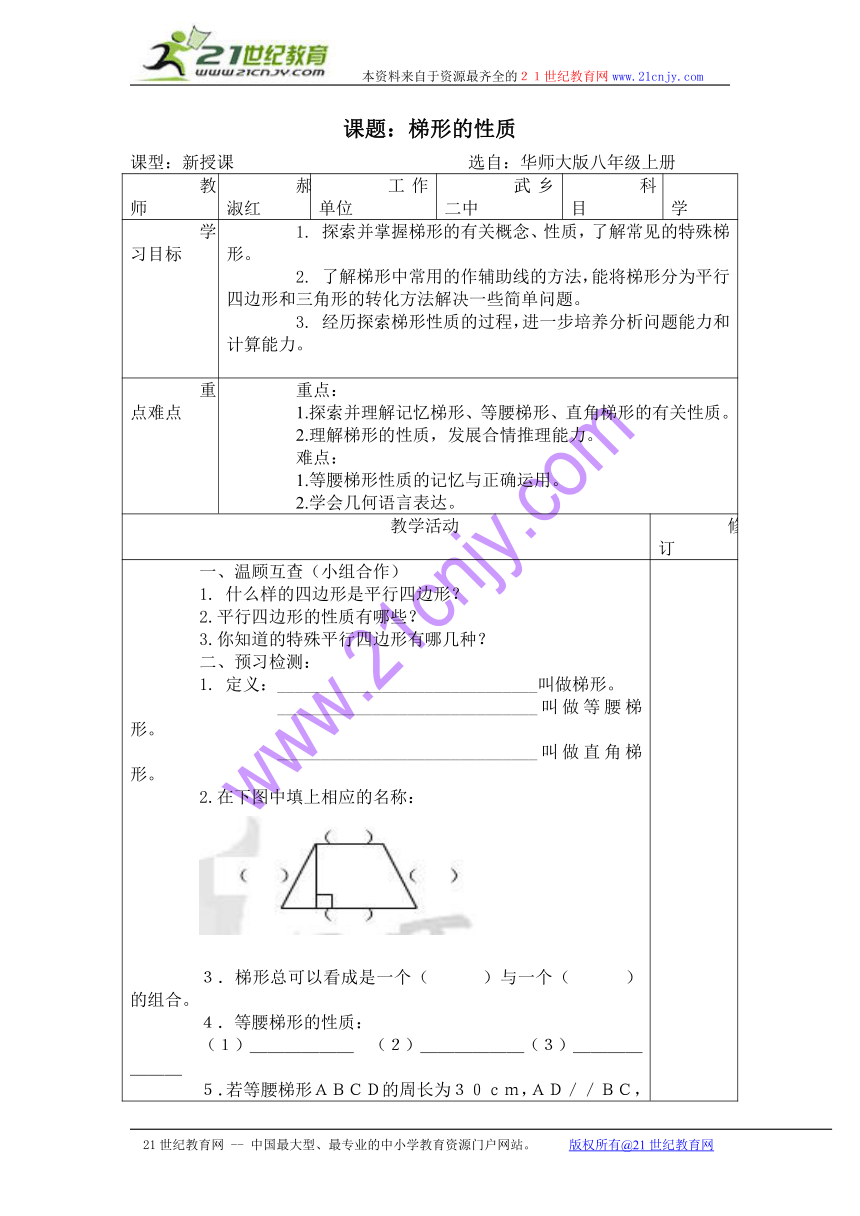
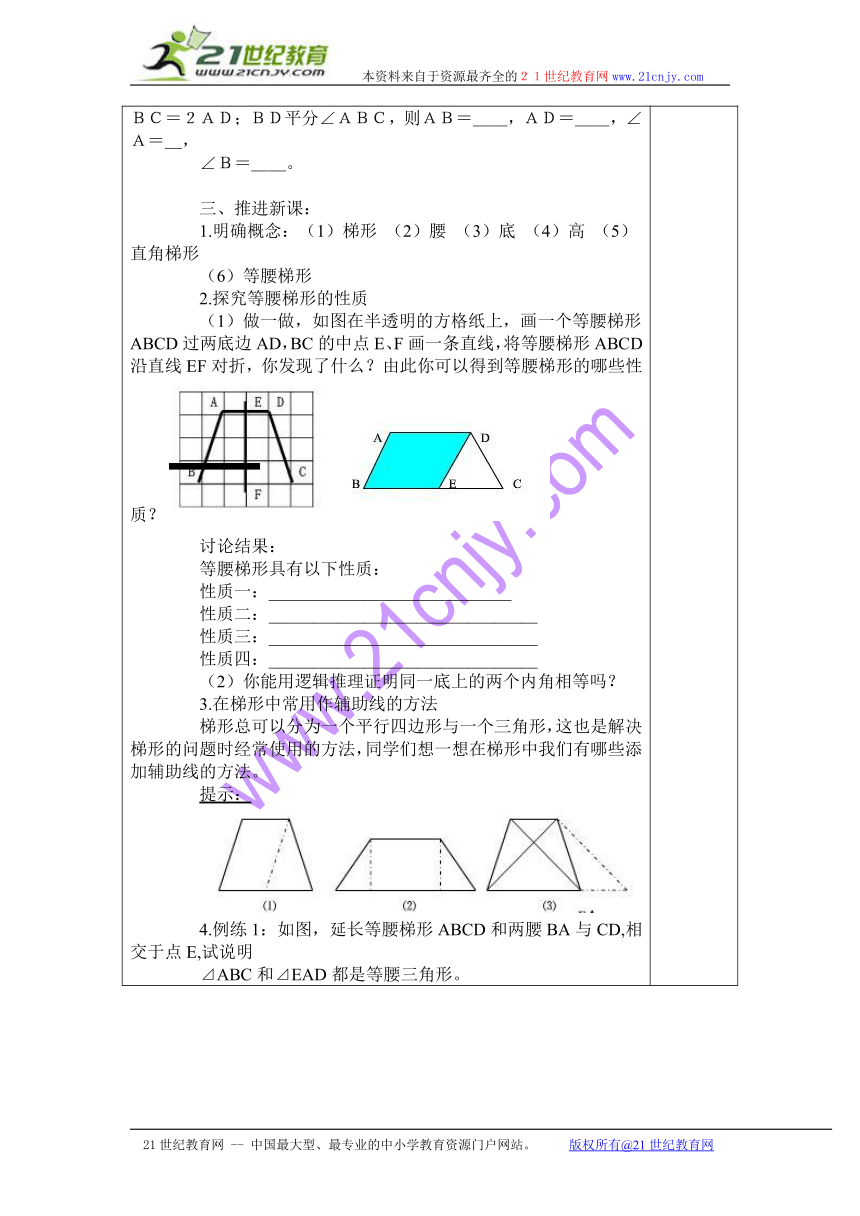
一、温顾互查(小组合作)1. 什么样的四边形是平行四边形?2.平行四边形的性质有哪些?3.你知道的特殊平行四边形有哪几种?二、预习检测:1. 定义:______________________________叫做梯形。 ______________________________叫做等腰梯形。 ______________________________叫做直角梯形。2.在下图中填上相应的名称:3.梯形总可以看成是一个( )与一个( ) 的组合。4.等腰梯形的性质: (1)______ (2)______(3)_______5.若等腰梯形ABCD的周长为30cm,AD//BC,BC=2AD;BD平分∠ABC,则AB=__,AD=__,∠A=_,∠B=__。三、推进新课:1.明确概念:(1)梯形 (2)腰 (3)底 (4)高 (5)直角梯形 (6)等腰梯形2.探究等腰梯形的性质(1)做一做,如图在半透明的方格纸上,画一个等腰梯形ABCD过两底边AD,BC的中点E、F画一条直线,将等腰梯形ABCD沿直线EF对折,你发现了什么?由此你可以得到等腰梯形的哪些性质?讨论结果:等腰梯形具有以下性质:性质一:____________________________ 性质二:_______________________________ 性质三:_______________________________ 性质四:_______________________________(2)你能用逻辑推理证明同一底上的两个内角相等吗?3.在梯形中常用作辅助线的方法梯形总可以分为一个平行四边形与一个三角形,这也是解决梯形的问题时经常使用的方法,同学们想一想在梯形中我们有哪些添加辅助线的方法。提示:4.例练1:如图,延长等腰梯形ABCD和两腰BA与CD,相交于点E,试说明⊿ABC和⊿EAD都是等腰三角形。例练1图 例练2图例练2:如图,在梯形ABCD中,AB//DC, DE//CB, ⊿AED的周长为18,EB=4, 求梯形的周长。四、学习检测:1、如图,梯形ABCD中,AD∥BC,AB=DC,则∠A= ∠C= 。2、如图,梯形ABCD中,AD∥BC,∠A:∠B=3:1,则∠A= 度。3、如图,梯形ABCD中,AD∥BC,AB=DC,若AC=3cm,则BD= cm4、已知等腰梯形的一个内角等于70°,则其他三个内角的度数是 。5、如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,AD=2,BC=4, ∠B=60°,则AB= 。6、如图,直角梯形ABCD中,∠B=90°,∠C=45°,AD=4,BC=10,则AB= ,CD= 。 7、如图,在等腰梯形ABCD中, AD∥BC,高DF =4,AD=4,BC=8,求SΔCDF 五、能力提高:已知梯形的上底长为2,下底长为5,一腰长为4,则另一腰长的取值范围是_____________.2. 已知,梯形ABCD中,AD∥BC, AB=DC, ∠B=600,AD=15,AB=45,求BC的长。六、小结:你学会了什么?你有什么收获和感受?还有什么疑惑?请写出来。——————————————————————————,——————————————————————————,——————————————————————————。
6题图
5题图
A
D
B
C
E
A
D
B
C
7题图
A
D
B
C
A
B
C
D
1
15
45
15
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
课题:梯形的性质
课型:新授课 选自:华师大版八年级上册
教师 郝淑红 工作单位 武乡二中 科目 数学
学习目标 1. 探索并掌握梯形的有关概念、性质,了解常见的特殊梯形。2. 了解梯形中常用的作辅助线的方法,能将梯形分为平行四边形和三角形的转化方法解决一些简单问题。3. 经历探索梯形性质的过程,进一步培养分析问题能力和计算能力。
重点难点 重点:1.探索并理解记忆梯形、等腰梯形、直角梯形的有关性质。2.理解梯形的性质,发展合情推理能力。难点:1.等腰梯形性质的记忆与正确运用。2.学会几何语言表达。
教学活动 修订
一、温顾互查(小组合作)1. 什么样的四边形是平行四边形?2.平行四边形的性质有哪些?3.你知道的特殊平行四边形有哪几种?二、预习检测:1. 定义:______________________________叫做梯形。 ______________________________叫做等腰梯形。 ______________________________叫做直角梯形。2.在下图中填上相应的名称:3.梯形总可以看成是一个( )与一个( ) 的组合。4.等腰梯形的性质: (1)______ (2)______(3)_______5.若等腰梯形ABCD的周长为30cm,AD//BC,BC=2AD;BD平分∠ABC,则AB=__,AD=__,∠A=_,∠B=__。三、推进新课:1.明确概念:(1)梯形 (2)腰 (3)底 (4)高 (5)直角梯形 (6)等腰梯形2.探究等腰梯形的性质(1)做一做,如图在半透明的方格纸上,画一个等腰梯形ABCD过两底边AD,BC的中点E、F画一条直线,将等腰梯形ABCD沿直线EF对折,你发现了什么?由此你可以得到等腰梯形的哪些性质?讨论结果:等腰梯形具有以下性质:性质一:____________________________ 性质二:_______________________________ 性质三:_______________________________ 性质四:_______________________________(2)你能用逻辑推理证明同一底上的两个内角相等吗?3.在梯形中常用作辅助线的方法梯形总可以分为一个平行四边形与一个三角形,这也是解决梯形的问题时经常使用的方法,同学们想一想在梯形中我们有哪些添加辅助线的方法。提示:4.例练1:如图,延长等腰梯形ABCD和两腰BA与CD,相交于点E,试说明⊿ABC和⊿EAD都是等腰三角形。例练1图 例练2图例练2:如图,在梯形ABCD中,AB//DC, DE//CB, ⊿AED的周长为18,EB=4, 求梯形的周长。四、学习检测:1、如图,梯形ABCD中,AD∥BC,AB=DC,则∠A= ∠C= 。2、如图,梯形ABCD中,AD∥BC,∠A:∠B=3:1,则∠A= 度。3、如图,梯形ABCD中,AD∥BC,AB=DC,若AC=3cm,则BD= cm4、已知等腰梯形的一个内角等于70°,则其他三个内角的度数是 。5、如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,AD=2,BC=4, ∠B=60°,则AB= 。6、如图,直角梯形ABCD中,∠B=90°,∠C=45°,AD=4,BC=10,则AB= ,CD= 。 7、如图,在等腰梯形ABCD中, AD∥BC,高DF =4,AD=4,BC=8,求SΔCDF 五、能力提高:已知梯形的上底长为2,下底长为5,一腰长为4,则另一腰长的取值范围是_____________.2. 已知,梯形ABCD中,AD∥BC, AB=DC, ∠B=600,AD=15,AB=45,求BC的长。六、小结:你学会了什么?你有什么收获和感受?还有什么疑惑?请写出来。——————————————————————————,——————————————————————————,——————————————————————————。
6题图
5题图
A
D
B
C
E
A
D
B
C
7题图
A
D
B
C
A
B
C
D
1
15
45
15
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
