2.3.2 二次函数与一元二次方程的联系
文档属性
| 名称 | 2.3.2 二次函数与一元二次方程的联系 |

|
|
| 格式 | rar | ||
| 文件大小 | 171.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-12-21 00:00:00 | ||
图片预览






文档简介
课件20张PPT。2.3.2 二次函数与一元二次方程的联系湖南省新邵县酿溪中学王军旗1、平面直角坐标系中,x轴上的点___坐标为0,y轴上的点____坐标为0.复习提问2、一元二次方程ax2+bx+c=0
(a≠0)的求根公式是什么?
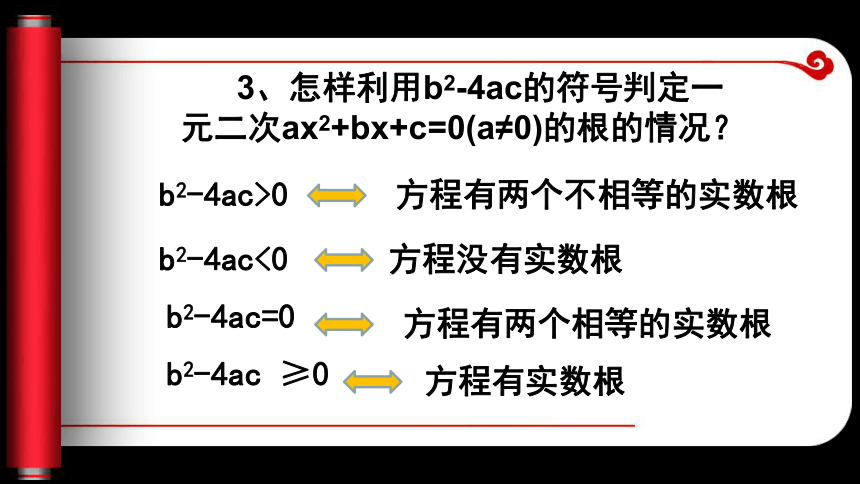
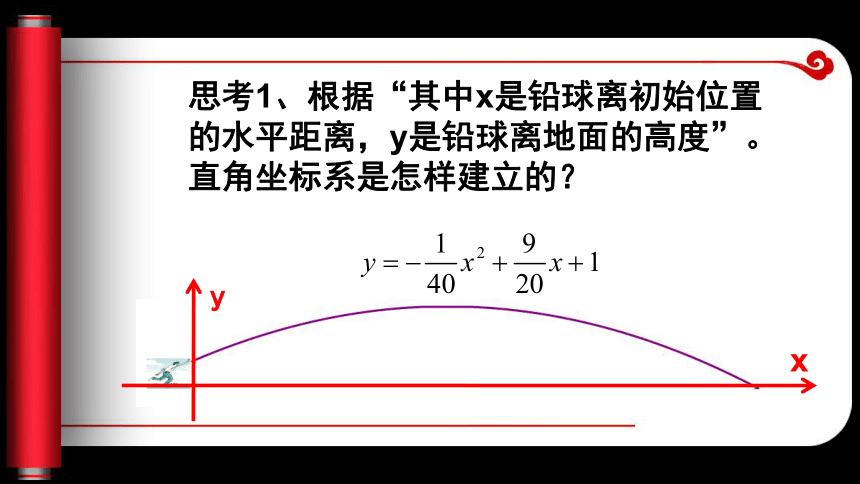
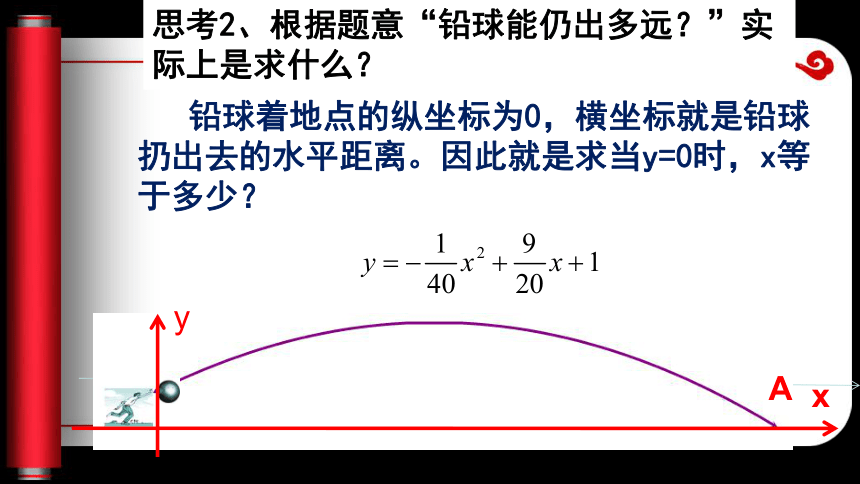
纵横(a,0)(0,b) 3、怎样利用b2-4ac的符号判定一元二次ax2+bx+c=0(a≠0)的根的情况? b2-4ac>0b2-4ac<0b2-4ac=0b2-4ac ≥0方程有两个不相等的实数根方程没有实数根方程有两个相等的实数根方程有实数根 掷铅球时,球在空中经过的路线是抛物线,已知某运动员掷铅球时,铅球在空中经过的抛物线解析式是: 其中x是铅球离初始位置的水平距离,y是铅球离地面的高度。如图,你能求出铅球能仍出多远吗? 动脑筋思考1、根据“其中x是铅球离初始位置的水平距离,y是铅球离地面的高度”。直角坐标系是怎样建立的?xy 铅球着地点的纵坐标为0,横坐标就是铅球扔出去的水平距离。因此就是求当y=0时,x等于多少?思考2、根据题意“铅球能仍出多远?”实际上是求什么?xyAx2-18x-40=0, x2-18x=40, x2-18x+92=40+92 (x-9)2=121, x-9=-11,或x-9=11, x1=-2(不合题意,舍去),x2=20 所以,球被仍出去20m远。思考3、上题中求铅球能扔出多远,就是求y=0时x的值,实际上就是求函数图像与x轴的交点A的横坐标。怎样求二次函数y=ax2+bx+c(a≠0)的图像与x轴的交点坐标呢xyA令y=0,解一元二次方程ax2+bx+c=0(a≠0),这个方程的解就是函数图像与x的交点的横坐标
求下列抛物线与x轴的交点的横坐标 (1) y=4x2+12x+5,(2) y=x2+2x+1 (3) y=x2+2x+2解(1) 4x2+12x+5=0这里a=4,b=12,c=5
,b2-4ac=122-4×4×5=144-80=64
试试看∴ x1=- 1/2,x2=-5/2∴ 抛物线y=4x2+12x+5与x的交点的横坐标为
-1/2,或-5/2(2) y=x2+2x+1解: (x+1)2=0,
x+1=±0,
∴x1=x2=-1
∴抛物线y=x2+2x+1与x轴的交点的横坐标为-1(3)y=x2+2x+2解:x2+2x+2=0
这里a=1,b=2,c=2,
b2-4ac=22-4×1×2=-4<0
此方程无解,所以,抛物线x2+2x+2=0与x轴没有交点。思考4、上面三条抛物线与x轴的交点有的有两个,有的只有一个,有的一个也没有,这是为什么呢? 因为上面三个方程的判别式的值的符号不同,所以根的个数也不同,而一元二次方程的根的个数等于抛物线与x轴的交点个数,因此上面三条抛物线与x轴的交点个数也不同。请看下面上面三个函数在同一坐标系中的图像。思考5、怎样判断抛物线y=ax2+bx+c与x轴的交点个数呢?b2-4ac<0b2-4ac=0b2-4ac ≥0抛物线与x轴有两个交点抛物线与x轴没有交点抛物线与x轴有一个交点抛物线与x轴有交点b2-4ac>0思考6、在上问题中,铅球在空中经过的抛物线是 ,当铅球离地面高度为 2m时,它离初始位置的水平距离是多少(精确大0.01m)?思考7、为什么铅球会有两处在同一高度呢?思考8、已知抛物线上点的纵坐标y的值,怎样求该点的横坐标x的值呢? 只要把y的值代入抛物线解析式,解一元二次方程,方程的解就是y的对应值。思考9、上面例子表明已知二次函数的函数值,求对应的自变量的值时,需要解一元二次方程,反过来,解一元二次方程能不能借助二次函数呢?【例】求一元二次方程x2-2x-1=0的解的近似值。【分析】这个方程的解就是函数y=x2-2x-1当函数值为0时自变量的值。也就是图像与x轴交点的横坐标。因此只要画出函数图像,利用图像找出交点的横坐标就ok了。练习:P 47 1,2,3 小结 1、一元二次方程ax2+bx+c=0的解是二次函数 y=ax2+bx+c的图像与x轴的交点横坐标。 2、知道二次函数y=ax2+bx+c的函数值y,就对应点自变量的值,只需要把y的值代入函数式解方程,方程的解就是y的对应值。 3、函数y=ax2+bx+c图像与x轴交点的横坐标就是方程ax2+bx+c=0的解的近似值。作业P 49 A 4,5,B 1,2,3.
(a≠0)的求根公式是什么?
纵横(a,0)(0,b) 3、怎样利用b2-4ac的符号判定一元二次ax2+bx+c=0(a≠0)的根的情况? b2-4ac>0b2-4ac<0b2-4ac=0b2-4ac ≥0方程有两个不相等的实数根方程没有实数根方程有两个相等的实数根方程有实数根 掷铅球时,球在空中经过的路线是抛物线,已知某运动员掷铅球时,铅球在空中经过的抛物线解析式是: 其中x是铅球离初始位置的水平距离,y是铅球离地面的高度。如图,你能求出铅球能仍出多远吗? 动脑筋思考1、根据“其中x是铅球离初始位置的水平距离,y是铅球离地面的高度”。直角坐标系是怎样建立的?xy 铅球着地点的纵坐标为0,横坐标就是铅球扔出去的水平距离。因此就是求当y=0时,x等于多少?思考2、根据题意“铅球能仍出多远?”实际上是求什么?xyAx2-18x-40=0, x2-18x=40, x2-18x+92=40+92 (x-9)2=121, x-9=-11,或x-9=11, x1=-2(不合题意,舍去),x2=20 所以,球被仍出去20m远。思考3、上题中求铅球能扔出多远,就是求y=0时x的值,实际上就是求函数图像与x轴的交点A的横坐标。怎样求二次函数y=ax2+bx+c(a≠0)的图像与x轴的交点坐标呢xyA令y=0,解一元二次方程ax2+bx+c=0(a≠0),这个方程的解就是函数图像与x的交点的横坐标
求下列抛物线与x轴的交点的横坐标 (1) y=4x2+12x+5,(2) y=x2+2x+1 (3) y=x2+2x+2解(1) 4x2+12x+5=0这里a=4,b=12,c=5
,b2-4ac=122-4×4×5=144-80=64
试试看∴ x1=- 1/2,x2=-5/2∴ 抛物线y=4x2+12x+5与x的交点的横坐标为
-1/2,或-5/2(2) y=x2+2x+1解: (x+1)2=0,
x+1=±0,
∴x1=x2=-1
∴抛物线y=x2+2x+1与x轴的交点的横坐标为-1(3)y=x2+2x+2解:x2+2x+2=0
这里a=1,b=2,c=2,
b2-4ac=22-4×1×2=-4<0
此方程无解,所以,抛物线x2+2x+2=0与x轴没有交点。思考4、上面三条抛物线与x轴的交点有的有两个,有的只有一个,有的一个也没有,这是为什么呢? 因为上面三个方程的判别式的值的符号不同,所以根的个数也不同,而一元二次方程的根的个数等于抛物线与x轴的交点个数,因此上面三条抛物线与x轴的交点个数也不同。请看下面上面三个函数在同一坐标系中的图像。思考5、怎样判断抛物线y=ax2+bx+c与x轴的交点个数呢?b2-4ac<0b2-4ac=0b2-4ac ≥0抛物线与x轴有两个交点抛物线与x轴没有交点抛物线与x轴有一个交点抛物线与x轴有交点b2-4ac>0思考6、在上问题中,铅球在空中经过的抛物线是 ,当铅球离地面高度为 2m时,它离初始位置的水平距离是多少(精确大0.01m)?思考7、为什么铅球会有两处在同一高度呢?思考8、已知抛物线上点的纵坐标y的值,怎样求该点的横坐标x的值呢? 只要把y的值代入抛物线解析式,解一元二次方程,方程的解就是y的对应值。思考9、上面例子表明已知二次函数的函数值,求对应的自变量的值时,需要解一元二次方程,反过来,解一元二次方程能不能借助二次函数呢?【例】求一元二次方程x2-2x-1=0的解的近似值。【分析】这个方程的解就是函数y=x2-2x-1当函数值为0时自变量的值。也就是图像与x轴交点的横坐标。因此只要画出函数图像,利用图像找出交点的横坐标就ok了。练习:P 47 1,2,3 小结 1、一元二次方程ax2+bx+c=0的解是二次函数 y=ax2+bx+c的图像与x轴的交点横坐标。 2、知道二次函数y=ax2+bx+c的函数值y,就对应点自变量的值,只需要把y的值代入函数式解方程,方程的解就是y的对应值。 3、函数y=ax2+bx+c图像与x轴交点的横坐标就是方程ax2+bx+c=0的解的近似值。作业P 49 A 4,5,B 1,2,3.
