2.3.3 优化问题

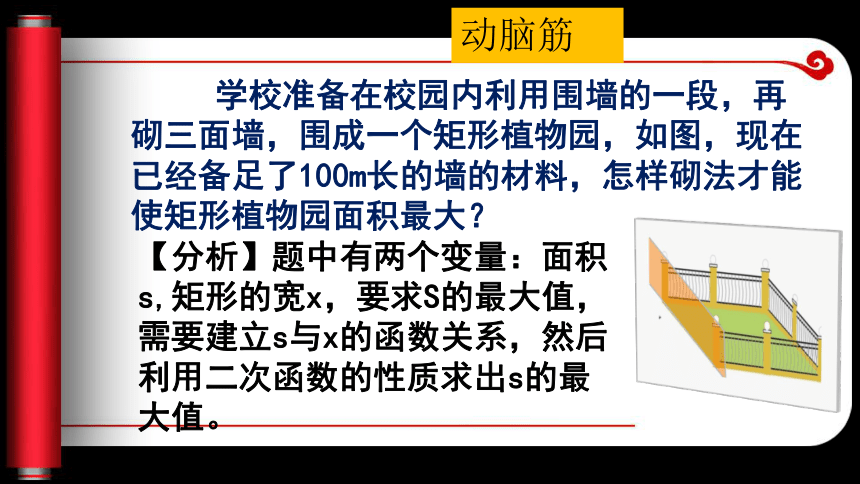
课件17张PPT。2.3.3 优化问题湖南省新邵县酿溪中学王军旗二次函数 y=ax2+bx+c总可以通过配方化为： y=a(x-h)2+k 的形式。（1）h= ,k= ___, ____ （2）当a>0时，开口向___,顶点最___,二次函数有____值，当x=____时，y的_____值是_____当a<0时，开口向___,顶点最___,二次函数有____值，当x=____时，y的_____值是_____复习提问上低小h小k下高大h最大k 学校准备在校园内利用围墙的一段，再砌三面墙，围成一个矩形植物园，如图，现在已经备足了100m长的墙的材料，怎样砌法才能使矩形植物园面积最大？动脑筋【分析】题中有两个变量：面积s,矩形的宽x，要求S的最大值，需要建立s与x的函数关系，然后利用二次函数的性质求出s的最大值。解：设与已有墙垂直的一面墙长为xm，则与已有墙平行的一面墙长为（100-2x)m.于是，S=X(100-2X)（0 =-2(x2-50x+252-252)
=-2(x-25) 2+1250
∴当x=25时，s达到最大值1250答：与已有墙垂直的一面墙25m，与已有墙平行的一面墙50m时，矩形面积最大，达到1250m 2思考：解优化问题的思路是什么？理解题意建立函数关系利用函数关系求最大（小）值分清题中有几个量是什么关系注意自变量的取值范围例1. （2009烟台） 某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施.调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台． （1）假设每台冰箱降价x元，商场每天销售这种冰箱的利润是y元，请写出y与x之间的函数表达式；（不要求写自变量的取值范围） （2）商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？ （3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？400-x400y根据题意，完成下表（2）商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？整理，得x2-300x+20000=0．
解这个方程，得x1=100,x2=200 要使百姓得到实惠，取x=200所以，每台冰箱
应降价200元．（3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？所以，每台冰箱的售价降价150元时，商场的利润最大，最大利润是5000元例2. (2008西宁市)现有一块矩形场地，如图1所示，长为40m，宽为30m，要将这块地划分为四块分别种植：A．兰花；B．菊花；C．月季；D．牵牛花．（1） 求出这块场地中种植B菊花的面积 与B场地的长X之间的函数关系式，并写出自为量的取值范围．（2）当x 是多少时，种植菊花的面积最大？最大面积是多少？（1）求出这块场地中种植B菊花的面积 与B场地的长X之间的函数关系式，并写出自为量的取值范围．解：（1）由题意知， 场地B宽为(30-X)m, ∴y=x(30-x)=-x2+30x,
∴ 自变量 的取值范围
为0 最大面积为225m2．1、（2010云南昭通）某种火箭被竖直向上发射时，它的高度h(m)与时间t(s)的关系可以用公式h=-5t2+150t+10表示．经过______s，火箭达到它的最高点．变式练习15 2、掷铅球时，球在空中经过的路线是抛物线 ,已知某运动员掷铅球时，铅球在空中经过的抛物线解析式是： 其中x是铅球离初始位置的水平距离，y是铅球离地面的高度。铅球在空中达到的最大高度是多少？变式练习 小结 解优化问题首先要仔细阅读题目，弄懂题意，明白题中有哪些量，各个量之间有什么关系，然后根据题意建立二次函数模型，根据二次函数性质求出最大值或最小值。作业：1、（2009年滨州市）某商品的进价为每件40元．当售价为每件60元时，每星期可卖出300件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出20件．在确保盈利的前提下，解答下列问题：（1）若设每件降价 x元、每星期售出商品的利润为 y元，请写出 y与x 的函数关系式，并求出自变量 的取值范围；（2）当降价多少元时，每星期的利润最大？最大利润是多少？2、P 53 2.