简几何体--球

课件24张PPT。简单几何体球知识清单1.球的概念及截面的性质；
2.球面距离；
3.地球上某地的经纬度；
4.球的体积与表面积；
5.球的组合体.球的概念 1.定义：半圆以它的直径为旋转轴旋转所成的曲面叫做球面，球面所围成的几何体叫球体，简称球. 2.球的元素：
（1）球心：球中形成球的半圆的圆心叫做球心；
（2）球的半径：连结球心和球面上任意一点的线段叫做球的半径；
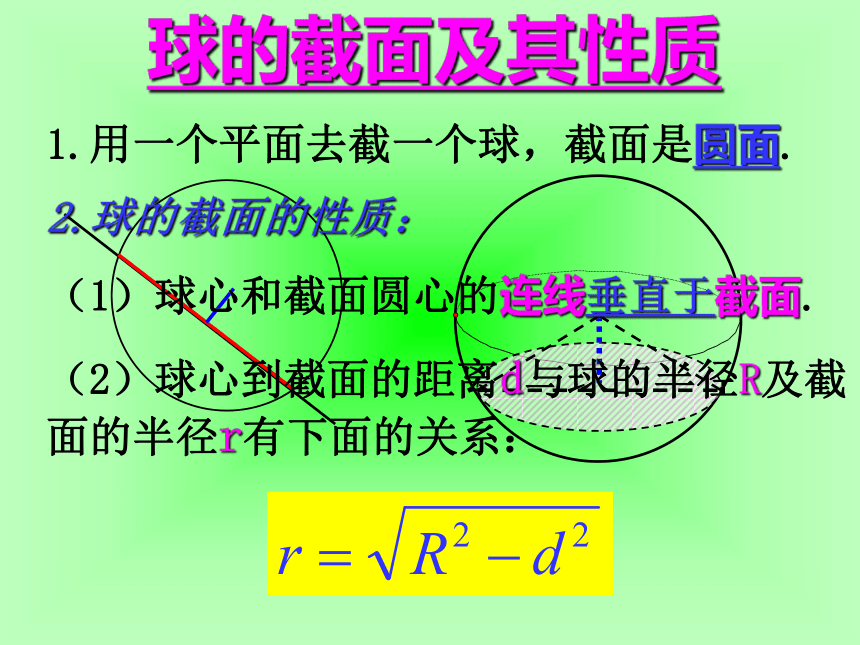
（3）球的直径：连结球面上两点并且经过球心的线段叫做球的直径.表示与定点的距离等于定长的点的集合球的截面及其性质1.用一个平面去截一个球，截面是圆面.2.球的截面的性质：
（1）球心和截面圆心的连线垂直于截面.
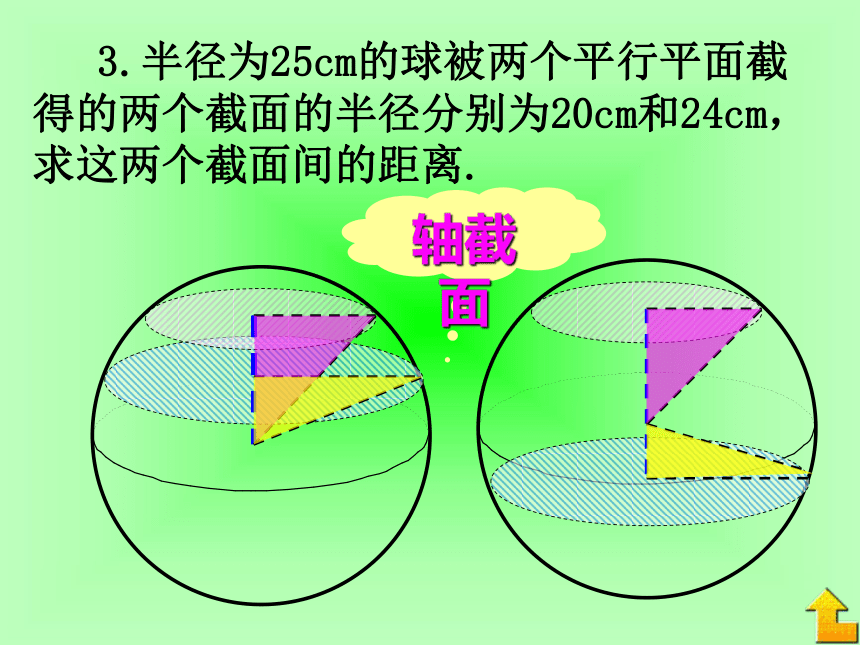
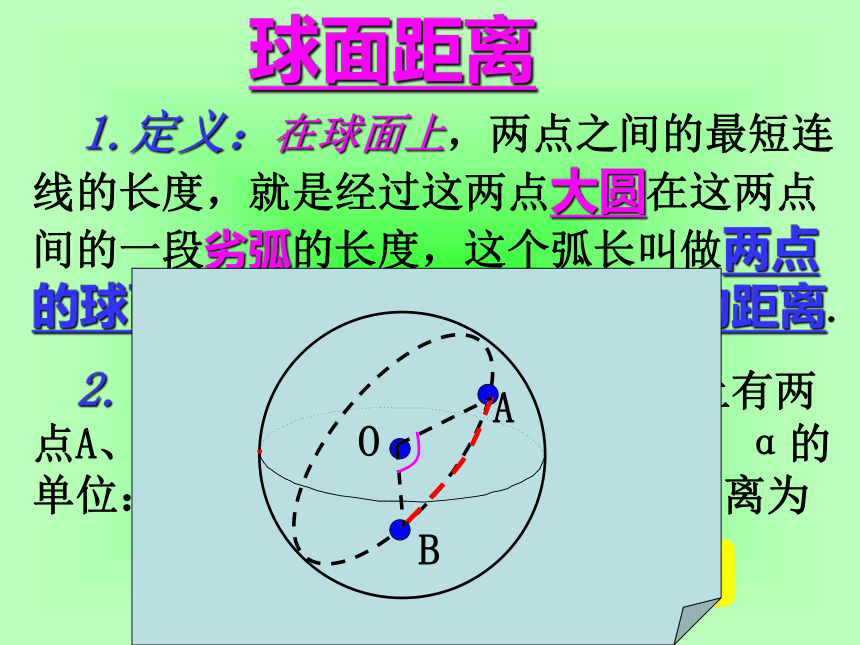
（2）球心到截面的距离d与球的半径R及截面的半径r有下面的关系：3.大圆与小圆（1）当d=0时r=R大圆 球面被经过球心的平面截得的圆叫做大圆；被不经过球心的平面所截得的圆叫做小圆.（2）当d=R时r=0（3）当0 l=α·R球心角ABO 1.A、B是半径为R的球面上的两点，它
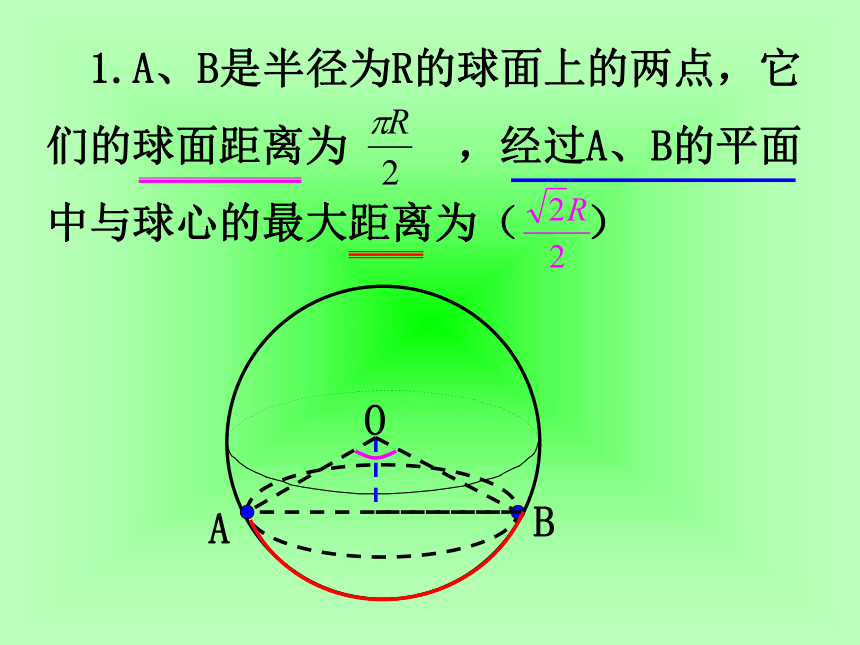
们的球面距离为 ，经过A、B的平面
中与球心的最大距离为（ ）OAB 2.球面上有三点，其中任意两点的球面距离都等于大圆周长的1/6，经过三点的小圆周长为4π，则这个球的半径为（ ）ABCOABCOO1地球上的经纬线北南 过南北两极的球的大圆为经度圈，其中过英国格林威治天文台的经线为0°经线（本初子午线），东西各分180°，东经180°与西经180°在同一条经线上，称180°经线. 地球的赤道为0°纬线圈，向南北各分90°，属于北纬与南纬.某地的经度 经过该地的经线与地轴确定的半平面和本初子午线与地轴确定的半平面所成的二面角的大小即为该地的经度.P北南OABA1B1O1即：∠AOB的大小某地的纬度 该地与球心的连线和赤道面所成的线面角的大小即为该地的纬度.北南POB即：∠POB的大小 1.北京位于东经116°，北纬40°
（1）在地球面上如何确定北京位置？
（2）求北纬40°的纬线长.（地球半径6370km）北南本初子午线116°40° 2.已知地球半径R，A、B两地均位于北纬45°线上，其经度差为90°.求（1）在北纬45°圈上劣弧AB的长度；（2）球面上A、B两点的距离.ABOO1BAOO1球的体积公式方法：分割、求近似和、求精确和半径为R的球的体积球的表面积公式半径为R的球的表面积 1.在一个底面半径为5cm的圆柱内浸没了两个直径5cm的玻璃球，若取出这两个球，求容器内的水面下降的高度.∴h=5/3 cm 2.球面上有A、B两点，它们的球面距离为5πcm，过这两个点的半径成60°角，求这个球的体积. 3.已知圆柱的底面直径与高都等于球的直径，求证：
（1）球的表面积等于圆柱的侧面积.
（2）球的表面积等于圆柱全面积的2/3. 解：设球的半径为R，则圆柱的底面半径为R，高为2R ∴S球=4πR2
S圆柱侧=4πR2
S圆柱全=6πR2 4.在球面上有四个点P、A、B、C，若PA、PB、PC两两互相垂直且PA=PB=PC=a。则这个球的表面积为（ ）.PABCO1OPCO1O3πa2正方体与球1. 正方体的内切球轴截面中心重合2R=a2. 正方体的外接球轴截面正四面体与球 正四面体的内切球外接球推广设正四面体棱长为a,则V=S表=∴r=BACDO 思考：一个球切于正方体的各
棱，若正方体的棱长为a，则球的半
径为（ ）？