24.1.3

课件14张PPT。学会老师教的
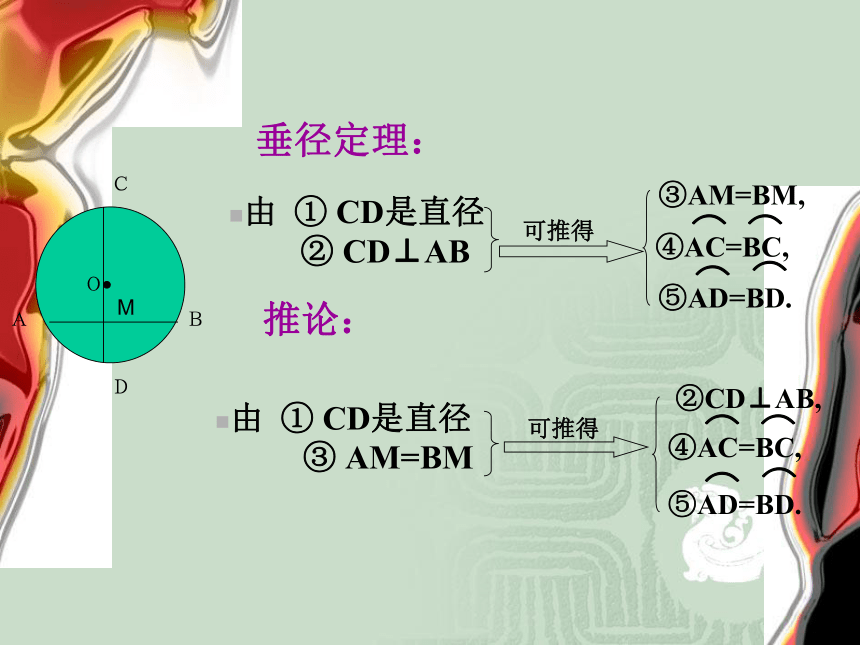
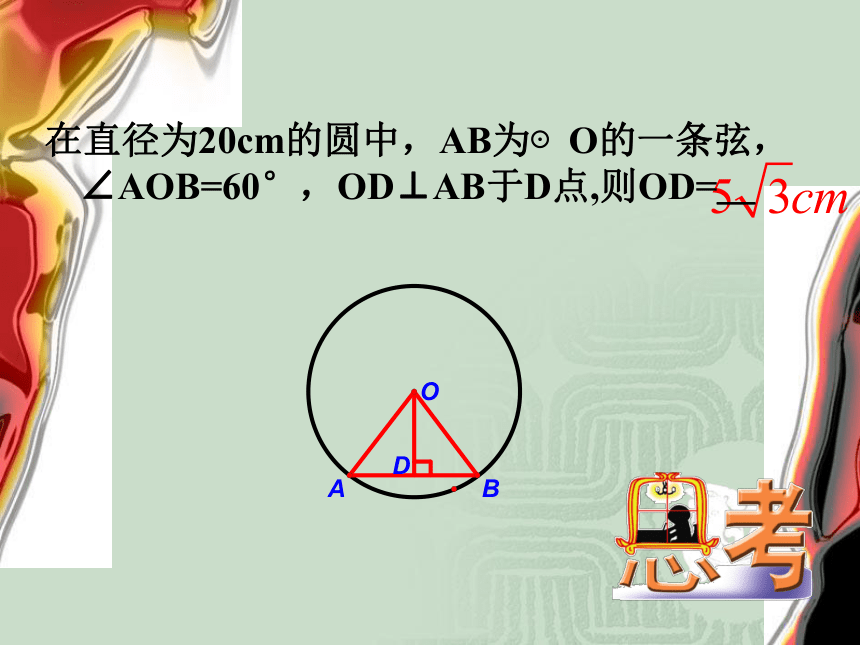
形 成自己用 的河北省怀来县桑园中学 古金龙垂径定理：推论：在直径为20cm的圆中，AB为⊙O的一条弦，
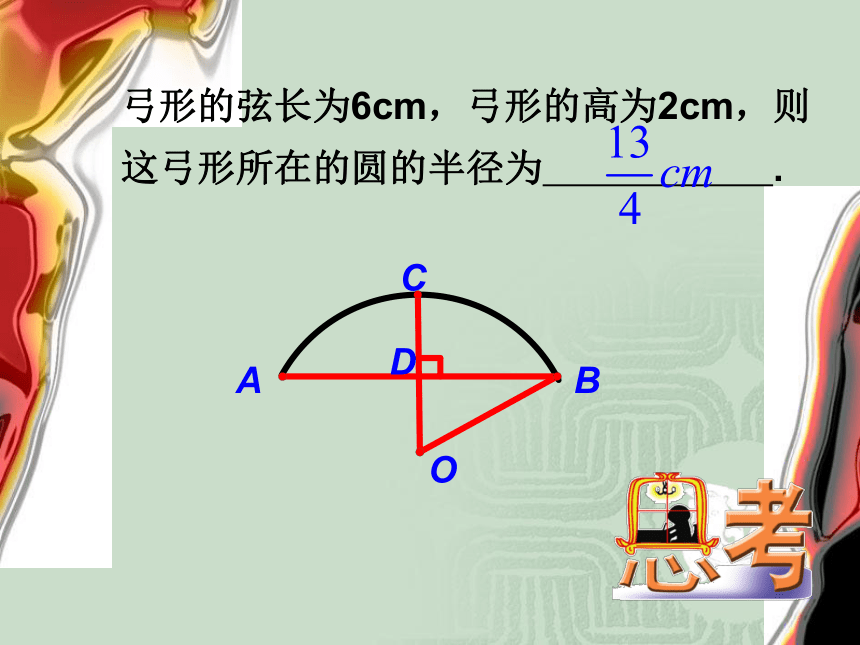
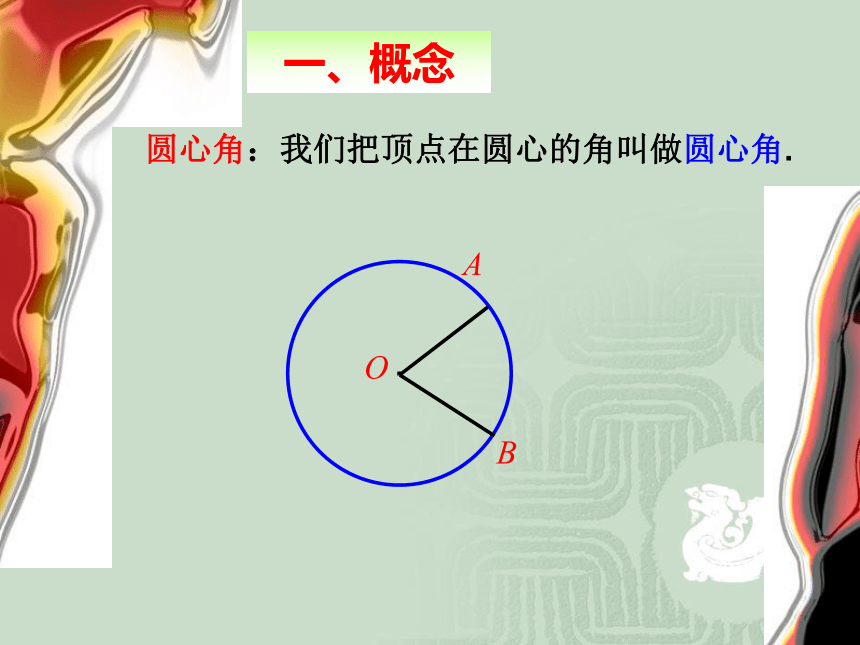
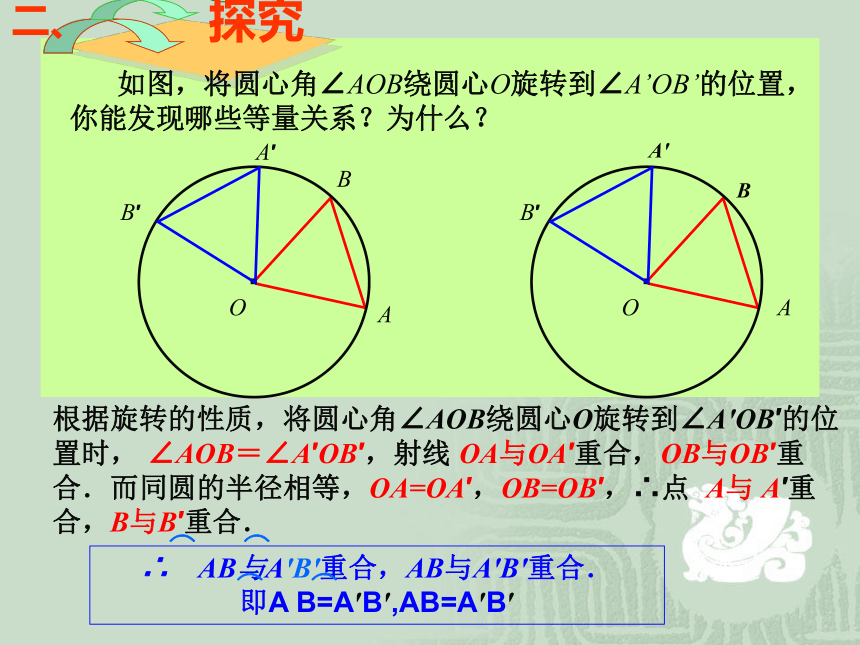
∠AOB=60°，OD⊥AB于D点,则OD=＿弓形的弦长为6cm，弓形的高为2cm，则这弓形所在的圆的半径为　　　　　　. 24.1.3 弧、弦、圆心角的关系· 圆心角：我们把顶点在圆心的角叫做圆心角.O一、概念根据旋转的性质，将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置时， ∠AOB＝∠A′OB′，射线 OA与OA′重合，OB与OB′重合．而同圆的半径相等，OA=OA′，OB=OB′，∴点 A与 A′重合，B与B′重合．·OAB·OABA′B′A′B′二、∴　AB与A′B′重合，AB与A′B′重合．
即A B=A′B′,AB=A′B′ 如图，将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置，你能发现哪些等量关系？为什么？⌒⌒⌒⌒在同圆或等圆中，相等的弧所对的圆心角_____， 所对的弦________；
在同圆或等圆中，相等的弦所对的圆心角______，所对的弧_________．弧、弦与圆心角的关系定理相等相等相等相等三、定理 如图，AB、CD是⊙O的两条弦．
（1）如果AB=CD，那么___________，_________________．
（2）如果 ，那么____________，_____________．
（3）如果∠AOB=∠COD，那么_____________，_________．
（4）如果AB=CD，OE⊥AB于E，OF⊥CD于F，OE与OF相等吗？为什么？AB=CDAB=CD四、迁移运用⌒⌒⌒⌒⌒⌒AB = CDAB=CDAB=CD证明：∴ AB=AC．又∠ACB=60°，∴ AB=BC=CA.∴ ∠AOB＝∠BOC＝∠AOC.·ABCO五、例题展示例1 如图, 在⊙O中， ，∠ACB=60°，
求证∠AOB=∠BOC=∠AOC.⌒⌒∵AB=ACAB=AC⌒⌒如图，AB是⊙O 的直径， ∠COD=35°，求∠AOE 的度数．解：六、同步练习⌒⌒⌒⌒⌒⌒∵BC = CD = DEBC=CD=DE
已知AB是⊙O的直径,M、N分别是AO和BO的中点，CM⊥AB，DN⊥AB，则弧AC和弧BD有什么关系？为什么？七.更上一层楼体会.分享说出你这节课的收获和体验，让大家与你一起分享！！！九、作业1、教材94－95页
　　　　2，3,　10，12
2、100闯关填空题别忘记我哟