用列举法求概率（1）

课件14张PPT。25.2. 用列举法求概率（1）复习引入 必然事件；
在一定条件下必然发生的事件，
不可能事件；
在一定条件下不可能发生的事件
随机事件；
在一定条件下可能发生也可能不发生的事件，概率的定义 0≤P(A) ≤1.
必然事件的概率是1，不可能事件的概率是0. 一般地，对于一个随机事件A，我们把刻画其发生可能性大小的数值，称为随机事件A的概率，记作P(A)。归纳：求随机事件A的概率的方法： 一般的，如果在一次试验中，有n种可能的结果，并且他们发生的可能性都相等，事件A包含其中的m种结果，那么事件A发生的概率P(A)=1．有5张数字卡片，它们的背面完全相同，正面分别标有1，2，2，3，4。现将它们的背面朝上，从中任意摸到一张卡片，则：p （摸到2号卡片）= ;p （摸到奇数号卡片）= ; P（摸到偶数号卡片） = .p （摸到1号卡片）= ;
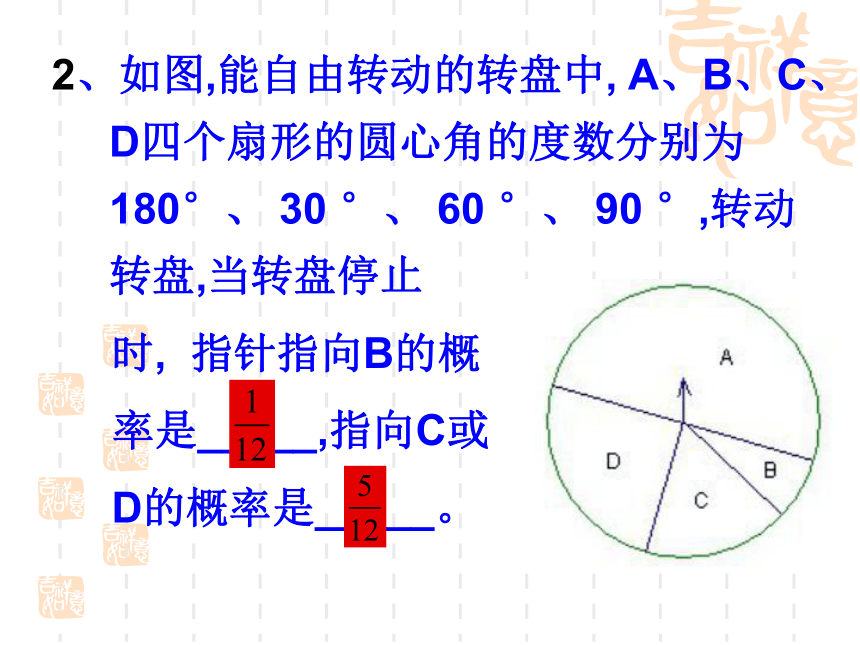
复习练习：2、如图,能自由转动的转盘中, A、B、C、D四个扇形的圆心角的度数分别为180°、 30 °、 60 °、 90 °,转动转盘,当转盘停止
时, 指针指向B的概
率是_____,指向C或
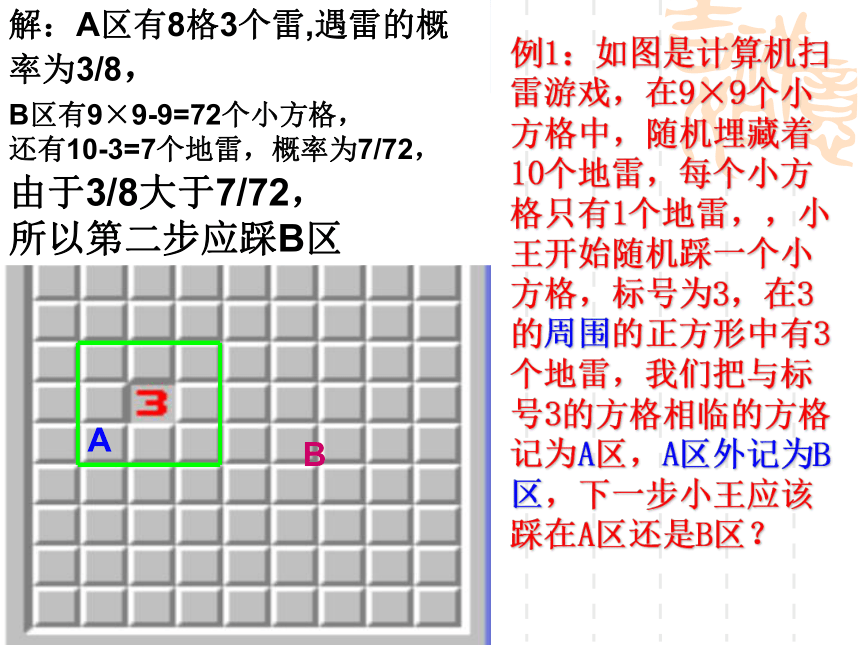
D的概率是_____。例1：如图是计算机扫雷游戏，在9×9个小方格中，随机埋藏着10个地雷，每个小方格只有1个地雷，，小王开始随机踩一个小方格，标号为3，在3的周围的正方形中有3个地雷，我们把与标号3的方格相临的方格记为A区，A区外记为B区，下一步小王应该踩在A区还是B区？由于3/8大于7/72，
所以第二步应踩B区解：A区有8格3个雷,遇雷的概率为3/8，B区有9×9-9=72个小方格，
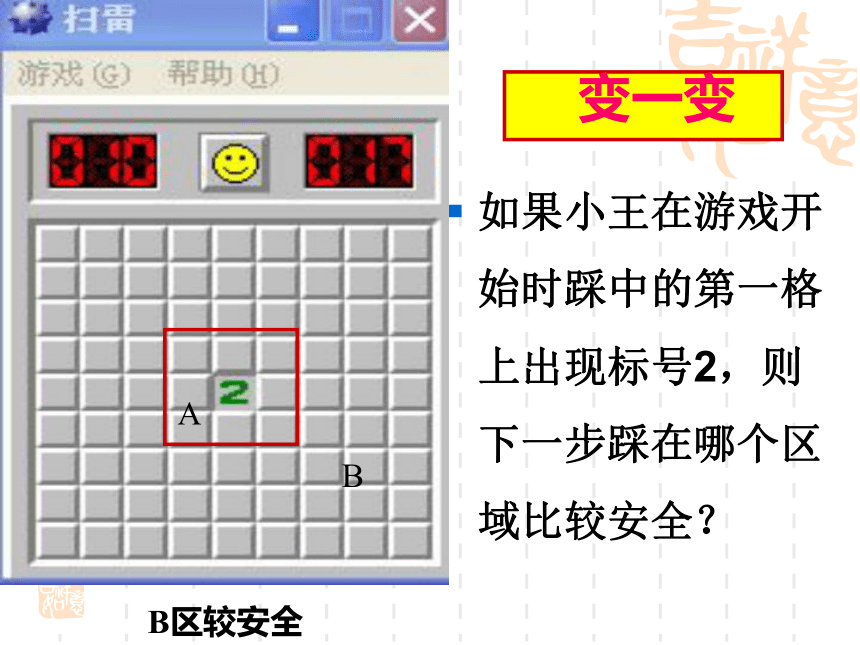
还有10-3=7个地雷，概率为7/72，AB变一变如果小王在游戏开始时踩中的第一格上出现标号2，则下一步踩在哪个区域比较安全？B区较安全问题:掷两枚硬币,怎样求下列事件的概率？
(1)两枚硬币全部正面朝上;
(2)两枚硬币全部反面朝上;
(3)一枚硬币正面朝上,一枚硬币反面朝上.解:其中一枚硬币为A,另一枚硬币为B,则所有可能结果如表所示:AB总共4种结果,每种结果出现的可能性相同.(1)所有结果中,满足两枚硬币全部正面朝上的结果只有一个,即”(正,正)”,所以
P(两枚硬币全部正面朝上)=回顾：掷一枚硬币，正面向上的概率是多少？(2)两枚硬币全部反面朝上;
(3)一枚硬币正面朝上,一枚硬币反面朝上.AB(2)所有结果中,满足两枚硬币全部反面朝上的结果只有一个,即”(反,反)”,所以
P(两枚硬币全部反面朝上)=(3)所有结果中,满足一枚硬币正面朝上, 一枚硬币反面朝上的结果有2个,即”(正,反),(反,正)”,所以
P(一枚硬币正面朝上,一枚硬币反面朝上)=如图,甲三等分数字转盘，乙是四等分数字转盘，同时自由转动两个转盘，当转盘停止转动后（指针指在边界时重转），问题1：两个转盘指针指向数字之和不超过4的概率是多少？
问题2：两个转盘指针指向数字之和超过4的概率是多少？
问题3：两个转盘指针指向数字之和为奇数的概率是多少？
问题：如图，由A村去B村的道路有三条，由B村去C村的道路有两条，（1）从A村经B村去C村有多少种不同的走法？（2）某人从中任选一条路线，选中“先经A—B中路，再经B—C南路”的概率是多少？（1）6种；
（2）1/6A村B村C村北南中北南要“玩”出水平“配紫色”游戏小颖为学校联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.(1)利用列表的方法表示游戏者所有可能出现的结果.
(2)游戏者获胜的概率是多少?
真知灼见源于实践表格可以是：“配紫色”游戏游戏者获胜的概率是1/6.黄蓝绿红(红,黄)(红,蓝)(红,绿)白(白,黄)(白,蓝)(白,绿) 当一次试验要涉及两个因素（例如
掷两个骰子）并且可能出现的结果数目较
多时，为不重不漏地列出所有可能结果，
通常采用列表法。课堂小结