连云港市2011届高三第一次调研考试
图片预览




文档简介
连云港市2011届高三第一次调研考试
数学试题
一.填空题
1.若复数,,其中i是虚数单位,则复数的虚部是 ▲ .
2.已知集合,,若,则实数a的取值范围是 ▲ .
3.若函数为奇函数,则实数 ▲ .
4.若抛物线的焦点坐标为,则抛物线的标准方程
是 ▲ .
5.从某项综合能力测试中抽取10人的成绩,统计如
下表,则这10人成绩的方差为 ▲ .
分数
5
4
3
2
1
人数
3
1
1
3
2
6.如图是一个算法的流程图,则最后输出的 ▲ .
7.已知直线:,:,若∥,则实数a的值是 ▲ .
8.一个质地均匀的正四面体(侧棱长与底面边长相等的正三棱锥)玩具的四个面上分别标有1,2,3,4这四个数字.若连续两次抛掷这个玩具,则两次向下的面上的数字之积为偶数的概率是 ▲ .
9.已知,,则 ▲ .
10.已知函数及其导函数的图象如图所示,
则曲线在点P处的切线方程是 ▲ .
11.在△ABC中,点M满足,若 ,则实数m的值为 ▲ .
12.设m,n是两条不同的直线,,,是三个不同的平面,给出下列命题:
①若,,则;
②若,,则;
③若,,则;
④若,,,则.
上面命题中,真命题的序号是 ▲ (写出所有真命题的序号)..w.w.k.s
13.若关于x的不等式的解集中的整数恰有2个,则实数a的取值范围 是 ▲ .
14.已知数列,满足,,,且对任意的正整数,当时,都有,则的值是 ▲ .
二、解答题:本大题共6小题,共计90分.请在答题卡指定位置内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
如图,在△ABC中,已知,,,是平分线.
(1)求证:;
(2)求的值.
16.(本小题满分14分)
如图,在四棱锥中,四边形是菱形,,且E,F分别是BC, CD的中点. 求证:
(1)EF∥平面;
(2)平面⊥平面.
17.(本小题满分14分)
在各项均为正数的等比数列中,已知,且,,成等差数列.
(1)求数列的通项公式;
(2)设,求数列的前n项和.
18.(本小题满分16分)
已知椭圆E:的左焦点为F,左准线与x轴的交点是圆C的圆心,圆C恰好经过坐标原点O,设G是圆C上任意一点.
(1)求圆C的方程;
(2)若直线FG与直线交于点T,且G为线段FT的中点,求直线FG被圆C所截得的弦长;
(3)在平面上是否存在定点P,使得?若存在,求出点P坐标;若不存在,请说明理由.
19.(本小题满分16分)
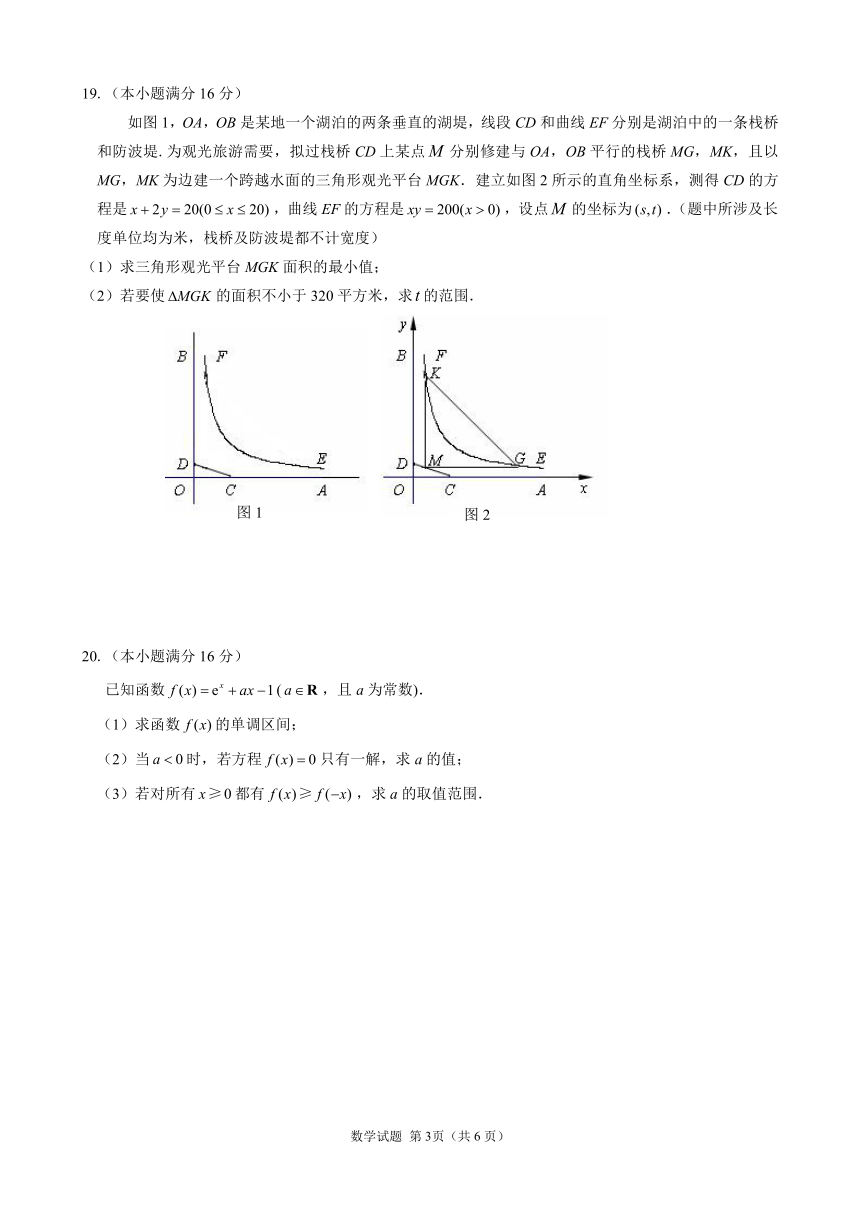
如图1,OA,OB是某地一个湖泊的两条垂直的湖堤,线段CD和曲线EF分别是湖泊中的一条栈桥和防波堤.为观光旅游需要,拟过栈桥CD上某点分别修建与OA,OB平行的栈桥MG,MK,且以MG,MK为边建一个跨越水面的三角形观光平台MGK.建立如图2所示的直角坐标系,测得CD的方程是,曲线EF的方程是,设点的坐标为.(题中所涉及长度单位均为米,栈桥及防波堤都不计宽度)
(1)求三角形观光平台MGK面积的最小值;
(2)若要使的面积不小于320平方米,求的范围.
20.(本小题满分16分)
已知函数(,且a为常数).
(1)求函数的单调区间;
(2)当时,若方程只有一解,求a的值;
(3)若对所有都有,求a的取值范围.
连云港市2011届高三第一次调研试卷
数学Ⅰ答案
一填空题:
1. 2, 2., 3., 4. , 5. , 6. 36, 7. , 8., 9.,
10. , 11. , 12. ②, 13., 14. 2012.
二、解答题
15.(1)在中,由正弦定理得①,
在中,由正弦定理得②, ………………………2分
又平分,
所以,,
,
由①②得,所以.………………………………………………6分
(2)因为,所以.
在△中,因为, …………10分
所以
.………………………………………………………14分
16.(1)因为E,F分别是BC,CD的中点,
所以EF∥BD,……………………………2分
因为EF平面PBD,BD平面PBD,
所以EF∥平面PBD.………………………6分
(2)设BD交AC于点O,连结PO,
因为ABCD是菱形,所以BD⊥AC,O是BD中点,
又,所以BD⊥PO,
又EF∥BD,所以EF⊥AC,EF⊥PO. ………………………10分
又,平面PAC,平面PAC,
所以EF⊥平面PAC.……………………………………………………………………12分
因为EF平面PEF,所以平面PEF⊥平面PAC.………………………………………14分
17.(1)设公比为q,由题意得,
且即 ……………………………………………2分
解之得或(舍去),…………………………………………………4分
所以数列的通项公式为,.…………………………………6分
(2)由(1)可得,所以.…………………………………8分
所以,
所以,
两式相减得,…………………………………10分
,
所以数列的前n项和为. ………………………………14分
18.(1)由椭圆E:,得:,,,
又圆C过原点,所以圆C的方程为.………………………………4分
(2)由题意,得,代入,得,
所以的斜率为,的方程为, …………………8分
(注意:若点G或FG方程只写一种情况扣1分)
所以到的距离为,直线被圆C截得弦长为.
故直线被圆C截得弦长为7.…………………………………………………………10分
(3)设,,则由,得,
整理得①,…………………………12分
又在圆C:上,所以②,
②代入①得, …………………………14分
又由为圆C 上任意一点可知,解得.
所以在平面上存在一点P,其坐标为. …………………………16分
19.(1)由题意,得, ,
又因为在线段CD:上,
所以,
……………4分
由,得,当且仅当,时等号成立.
……………………………………6分
令,则,.
又,故在上单调递减,
(注意:若在上单调递减未证明扣1分)
所以,此时,.
所以三角形MGK面积的最小值为225平方米. ……………………………………10分
(2)由题意得,
当,解得或(舍去),
由(1)知, ……………………………………14分
即,解之得.
所以的范围是.………………………………………………………16分
20.(1),………………………………………………………………1分
当时,,在上是单调增函数.…………………3分
当时,
由,得,在上是单调增函数;
由,得,在上是单调减函数.
综上,时,的单调增区间是.
时,的单调增区间是,单调减区间是.…6分
(2)由(1)知,当,时,最小,即,
由方程只有一解,得,又考虑到,
所以,解得.…………………………………………………10分
(3)当时,恒成立,
即得恒成立,即得恒成立,
令(),即当时,恒成立.
又,且,当时等号成立.
………………………………………………………………………………………12分
①当时,,
所以在上是增函数,故恒成立.
②当时,若,,
若,,
所以在上是增函数,故恒成立.…………………14分
③当时,方程的正根为,
此时,若,则,故在该区间为减函数.
所以,时,,与时,恒成立矛盾.
综上,满足条件的的取值范围是.……………………………………16分
2011届高三第一次调研考试数学命题意图与讲评建议
各位老师:
此次数学命题是全部高中学数学学习内容,在学校做教师时,我也不赞同全部考查,认为未复习考什么,考查当学意义比较在,但近几年的认识有所转变。未复习考查的是最基本的基础知识、基本方法、基本思想、基本经验,是学生在头脑中留下最本源东西。大家知道,高考必定有些内容是高三复习不到的内容,所以我个人已接受此时考试的价值。对于附加题主要是出于两个方面考虑,一是高二刚学习过的内容,学生忘的不多,且高二时又没有统考,另一方面是附加题部分很多学校都在平时顺带复习的,既然是考试总有学生看一看,考后老师讲一讲,所以附加题考虑再三还是坚持考查。但由于学生并未复习多少内容,理科主要是复习函数、导数、三角函数,三角函数复习也不多,所以命题内容侧重一点函数内容,相对公平,如最后两题都是函数与导数内容,填空题中也考查了三道函数题,第一题考了解三角形。其它内容重在基础知识、基本方法、基本思想的考查,没有涉及到解题技巧,注重考查数学的本质,同时对数学运算量也作了控制,从命之初到打磨成题,对运算量一降再降,但从高考角度,运算总是回避不了的,所以运算能力也许依法是学生首先要解决的问题,没有运算能力数学考试无从谈起。有些试题现在的成题,与当初命思想已有很大差别,现从命题的设想及试题演变角度思考,给出试题讲评建议(仅是个人考虑),供大家讲评时参考,不当之处,请批评。
1.若复数,,其中i是虚数单位,则复数的虚部是 ▲ .
讲评建议:求解过程,体现复数的虚部形成过程,抓住解决问题的本质思维,因此并不需要全部乘开,引导学生做题,小题也要体现思维的简捷性,当然,两复数相除,积模,模积,其模大小,几何意义,若能涉及也要涉及,扩大试题的功能,到复习复数时可以节省时间,复习本身就是一个整合的过程,是一个联系过程,需将每一个知识点放在整个高中数学体系中思考,思考其可能出现情况。
2.已知集合,,若,则实数a的取值范围是 ▲ .
讲评建议:此题当初是求自然数a的范围,但又怕学生不注意“自然数”出错,背离考查集合交集概念的初衷,所以改成求实数a的取值范围。一种集合是区间形式,一种是集合形式,一种是连续,一种是有限三个数,放在一起有的学生可能不习惯。
变式思考,改成,求其范围,又增加难度,但更有意思。
3.若函数为奇函数,则实数 ▲ .
讲评建议:函数是奇函数,且在有意义,即有,很多同学都知道,讲评中要反复强调函数在一定要有意义,且要讲解“,若函数为奇函数,求”,同时考虑讲解“”。此题对我们教学冲击很大,也说明教学研究是无此境的,教师教学要加强研究,不能停留在原有思维层次上,要研究方法不可用情况,特殊情况,越是定势思维,越要注意进行全面研究。2009年南通考了一题用出问题的,大家不妨查一下,对照讲解。
4.若抛物线的焦点坐标为,则抛物线的标准方程
是 ▲ .
5.从某项综合能力测试中抽取10人的成绩,统计如
下表,则这10人成绩的方差为 ▲ .
分数
5
4
3
2
1
人数
3
1
1
3
2
6.如图是一个算法的流程图,则最后输出的 ▲ .
7.已知直线:,:,若∥,则实数a的值是 ▲ .
讲评建议:教材课后有结论,对应成比例,先求后证,这与向量的平行垂直是一致的,联系讲解,让学生构成统一系统,易于应用时调取,容于易混时比较。
8.一个质地均匀的正四面体(侧棱长与底面边长相等的正三棱锥)玩具的四个面上分别标有1,2,3,4这四个数字.若连续两次抛掷这个玩具,则两次向下的面上的数字之积为偶数的概率是 ▲ .
9.已知,,则 ▲ .
讲评建议:此题重在变角公式的应用,当然很简单,这也是学生必须学会的解题技巧,三角函数变换要求在新课标中已有很大的降低,但这样的要注还是需的,若对已知展开用方程思想求解,也应是好方法,也要给予鼓励,从方程角度思考,问题就是解个方程,在差的学生也能会,也许这就是通法。考试时学生可能首先想到的就是“笨”方法,巧方法在那样紧张的环境下很难想出来。
10.已知函数及其导函数的图象如图所示,
则曲线在点P处的切线方程是 ▲ .
讲评建议:此题也体现着解决问题的本质思想,求一个函数在某点处
的切线方程的关键是什么,当然是某点的坐标及此点的导数值,有了
这样的分析此题就太简单了,也许这就是高考想要的思相方法。此题
可能出现的问题是由于导函数是一次函数,原函数是二次函数,学生
会求两个函数,再求切线方程,既走了回路。放在第10题也正是这种用意。
11.在△ABC中,点M满足,若 ,则实数m的值为 ▲ .
讲评建议:一种思维是对已知向量向目标向量分解,一种思维是理解已知向量条件的几何意义,既点M是三角形ABC的重心,再结合,三角形向量的中线形式,此问题观察即可解决,所以掌握相关结论,有了结论便利于联想。
12.设m,n是两条不同的直线,,,是三个不同的平面,给出下列命题:
①若,,则;
②若,,则;
③若,,则;
④若,,,则.
上面命题中,真命题的序号是 ▲ (写出所有真命题的序号)..w.w.k.s
13.若关于x的不等式的解集中的整数恰有2个,则实数a的取值范围 是 ▲ .
讲评建议:解决此题最好的方法是观察,故对条件两边开方,化为,再转化为函数数形结合解决,当然其它的方法也还是有的,教学中有必要展示学生解法,以体现学生的创造性。绝对值函数教学中要引起重视,绝对值函数即是分段函数。从二次函数角度也可以解决,主要是让学生了解决抛物线开口大小的是二次项系数绝对值的大小。若硬解二次不等式,会者也可解之,或直接解一次不等式,等等。
14.已知数列,满足,,,且对任意的正整数,当时,都有,则的值是 ▲ .
讲评建议:遇到这样一个新问题,学生首先应是先去归纳,找规律,这就是一种数学意识,解题意识,教学中要注意培养,如什么时候类比,什么时候归纳。
二、解答题:本大题共6小题,共计90分.请在答题卡指定位置内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
如图,在△ABC中,已知,,,是平分线.
(1)求证:;
(2)求的值.
讲评建议:此题第一问题是关于角平分线性质定理内容,但又是正弦定理的下接应用,考查时主要考虑到学生只有及少数知道角平分线,但教材没有给出角平分线定理,而且用平面几何知识证明,也不容易,题目中也没提及角平分线,主要是让大家重视教材中的例习题,(2)要注重两向量的夹角问题,这常是学生易犯的错误,借此引起学生的重视。当初命制此题是已知,且知的值,第一求,第二求,第三求,这样再求时,除直接用余弦定理求夹角,还可以考虑用向量分解方法求解,而且运算比较简单,但第二问运算量又太大了,为了让学生尽可能得分,所以改成考试试题形式。因此此题求解给教师的教学留出了较大空间,希望各位教师尽时挖掘。
(刚才学生考试,我恰好看了一下,当初怕学生第一题做不好,果然很多学生不会,教师反映,复习只用教辅,不用课本,书上的题不讲,教学必将走入误区,借此因起教师的高度重视,教学复习要教给学生什么,而不仅仅是做题。)
16.(本小题满分14分)
如图,在四棱锥中,四边形是菱形,,且E,F分别是BC, CD的中点. 求证:
(1)EF∥平面;
(2)平面⊥平面.
讲评建议:此题当初是如图情景,最后主要是考虑辅助线太多,
而且两问题之间辅助线滑有联系,同时考虑第二问题难度较大,
所以改成现在形式,希望各位教师讲评时还原本题的原来面目,
同时对第二问题要给予高度重视,主要平面几何的转化思想,
但对高一的求高复习中也要重视,高是教材中要求的。
17.(本小题满分14分)
在各项均为正数的等比数列中,已知,且,,成等差数列.
(1)求数列的通项公式;
(2)设,求数列的前n项和.
此题当初是:是考查学生最基础知识。当初是改变数字,求的前项的和。但考虑到分类讨论,可能比现在还繁,故改为现在情况,重点考查,等差数列、等比数列的基础知识。
18.(本小题满分16分)
已知椭圆E:的左焦点为F,左准线与x轴的交点是圆C的圆心,圆C恰好经过坐标原点O,设G是圆C上任意一点.
(1)求圆C的方程;
(2)若直线FG与直线交于点T,且G为线段FT的中点,求直线FG被圆C所截得的弦长;
(3)在平面上是否存在定点P,使得?若存在,求出点P坐标;若不存在,请说明理由.
讲评建议:对于第二问题当初是仿照2004年江苏高考题命制,用,考查两解情况,后改为,但综合全题还是有一线教师认为运算量较大,后改为现在情况,改成中点后,命题思想完全发生了变化,改成中点,学生用中点坐标公式,是代数方法,而原来思维是方程思想,这一点引起各位注意,对于第三问,也是教材的习题,逆向思维,同时是对两个参量求最值,学生一般接触较少,当然此题也可转化成一个参数,即对平方法,两次用圆方程消元,达到目的,建议教师讲解。同时注意到,此圆是以椭圆的左准线的与x轴的交点为圆心,两个定点恰是椭圆的左右焦点,三问题之间非常和谐,融为一体。
19.(本小题满分16分)
如图1,OA,OB是某地一个湖泊的两条垂直的湖堤,线段CD和曲线EF分别是湖泊中的一条栈桥和防波堤.为观光旅游需要,拟过栈桥CD上某点分别修建与OA,OB平行的栈桥MG,MK,且以MG,MK为边建一个跨越水面的三角形观光平台MGK.建立如图2所示的直角坐标系,测得CD的方程是,曲线EF的方程是,设点的坐标为.(题中所涉及长度单位均为米,栈桥及防波堤都不计宽度)
(1)求三角形观光平台MGK面积的最小值;
(2)若要使的面积不小于320平方米,求的范围.
讲评建议:此题当初(1)是求的最小值,
但两问题过于孤单,且不好设问题,另外量太大了,
两个模型。后只保留现在的(1),但作为倒数第二题,
份量又轻了,最后设计成现在的形式。
对于(2)可以解两次不等式,也可以利用(1)中的单调性,
解一次方程,解一次不等式,建议大家解一次方程,解一次不等式,
因为(1)中提供条件、得出的结论要考虑(2)是否需要。
讲评中求的最小值最好加上去。
20.(本小题满分16分)
已知函数(,且a为常数).
(1)求函数的单调区间;
(2)当时,若方程只有一解,求a的值;
(3)若对所有都有,求a的取值范围.
讲评建议:此题当初是(1)只有一解,求a的范围,大家感觉,作为(1)起点太高,学生不易得分,且上来讨论,又两问题都求范围可以,但还是单调形式单调,后改为现在形式。对于(3)主要是想改变教学中老师不研究情况,分参法是解决参数的一种好方法,但不唯一,且有时其方法不好图象快,如在区间是恒小于,用图象法就很快,同时也要注意到解决参数问题还有很多求不出最值问题。如本题,分参后求不出函数的最值,而且很多参数的范围是求不出来的,是对关键点进行分类讨论求得的。
数学试题
一.填空题
1.若复数,,其中i是虚数单位,则复数的虚部是 ▲ .
2.已知集合,,若,则实数a的取值范围是 ▲ .
3.若函数为奇函数,则实数 ▲ .
4.若抛物线的焦点坐标为,则抛物线的标准方程
是 ▲ .
5.从某项综合能力测试中抽取10人的成绩,统计如
下表,则这10人成绩的方差为 ▲ .
分数
5
4
3
2
1
人数
3
1
1
3
2
6.如图是一个算法的流程图,则最后输出的 ▲ .
7.已知直线:,:,若∥,则实数a的值是 ▲ .
8.一个质地均匀的正四面体(侧棱长与底面边长相等的正三棱锥)玩具的四个面上分别标有1,2,3,4这四个数字.若连续两次抛掷这个玩具,则两次向下的面上的数字之积为偶数的概率是 ▲ .
9.已知,,则 ▲ .
10.已知函数及其导函数的图象如图所示,
则曲线在点P处的切线方程是 ▲ .
11.在△ABC中,点M满足,若 ,则实数m的值为 ▲ .
12.设m,n是两条不同的直线,,,是三个不同的平面,给出下列命题:
①若,,则;
②若,,则;
③若,,则;
④若,,,则.
上面命题中,真命题的序号是 ▲ (写出所有真命题的序号)..w.w.k.s
13.若关于x的不等式的解集中的整数恰有2个,则实数a的取值范围 是 ▲ .
14.已知数列,满足,,,且对任意的正整数,当时,都有,则的值是 ▲ .
二、解答题:本大题共6小题,共计90分.请在答题卡指定位置内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
如图,在△ABC中,已知,,,是平分线.
(1)求证:;
(2)求的值.
16.(本小题满分14分)
如图,在四棱锥中,四边形是菱形,,且E,F分别是BC, CD的中点. 求证:
(1)EF∥平面;
(2)平面⊥平面.
17.(本小题满分14分)
在各项均为正数的等比数列中,已知,且,,成等差数列.
(1)求数列的通项公式;
(2)设,求数列的前n项和.
18.(本小题满分16分)
已知椭圆E:的左焦点为F,左准线与x轴的交点是圆C的圆心,圆C恰好经过坐标原点O,设G是圆C上任意一点.
(1)求圆C的方程;
(2)若直线FG与直线交于点T,且G为线段FT的中点,求直线FG被圆C所截得的弦长;
(3)在平面上是否存在定点P,使得?若存在,求出点P坐标;若不存在,请说明理由.
19.(本小题满分16分)
如图1,OA,OB是某地一个湖泊的两条垂直的湖堤,线段CD和曲线EF分别是湖泊中的一条栈桥和防波堤.为观光旅游需要,拟过栈桥CD上某点分别修建与OA,OB平行的栈桥MG,MK,且以MG,MK为边建一个跨越水面的三角形观光平台MGK.建立如图2所示的直角坐标系,测得CD的方程是,曲线EF的方程是,设点的坐标为.(题中所涉及长度单位均为米,栈桥及防波堤都不计宽度)
(1)求三角形观光平台MGK面积的最小值;
(2)若要使的面积不小于320平方米,求的范围.
20.(本小题满分16分)
已知函数(,且a为常数).
(1)求函数的单调区间;
(2)当时,若方程只有一解,求a的值;
(3)若对所有都有,求a的取值范围.
连云港市2011届高三第一次调研试卷
数学Ⅰ答案
一填空题:
1. 2, 2., 3., 4. , 5. , 6. 36, 7. , 8., 9.,
10. , 11. , 12. ②, 13., 14. 2012.
二、解答题
15.(1)在中,由正弦定理得①,
在中,由正弦定理得②, ………………………2分
又平分,
所以,,
,
由①②得,所以.………………………………………………6分
(2)因为,所以.
在△中,因为, …………10分
所以
.………………………………………………………14分
16.(1)因为E,F分别是BC,CD的中点,
所以EF∥BD,……………………………2分
因为EF平面PBD,BD平面PBD,
所以EF∥平面PBD.………………………6分
(2)设BD交AC于点O,连结PO,
因为ABCD是菱形,所以BD⊥AC,O是BD中点,
又,所以BD⊥PO,
又EF∥BD,所以EF⊥AC,EF⊥PO. ………………………10分
又,平面PAC,平面PAC,
所以EF⊥平面PAC.……………………………………………………………………12分
因为EF平面PEF,所以平面PEF⊥平面PAC.………………………………………14分
17.(1)设公比为q,由题意得,
且即 ……………………………………………2分
解之得或(舍去),…………………………………………………4分
所以数列的通项公式为,.…………………………………6分
(2)由(1)可得,所以.…………………………………8分
所以,
所以,
两式相减得,…………………………………10分
,
所以数列的前n项和为. ………………………………14分
18.(1)由椭圆E:,得:,,,
又圆C过原点,所以圆C的方程为.………………………………4分
(2)由题意,得,代入,得,
所以的斜率为,的方程为, …………………8分
(注意:若点G或FG方程只写一种情况扣1分)
所以到的距离为,直线被圆C截得弦长为.
故直线被圆C截得弦长为7.…………………………………………………………10分
(3)设,,则由,得,
整理得①,…………………………12分
又在圆C:上,所以②,
②代入①得, …………………………14分
又由为圆C 上任意一点可知,解得.
所以在平面上存在一点P,其坐标为. …………………………16分
19.(1)由题意,得, ,
又因为在线段CD:上,
所以,
……………4分
由,得,当且仅当,时等号成立.
……………………………………6分
令,则,.
又,故在上单调递减,
(注意:若在上单调递减未证明扣1分)
所以,此时,.
所以三角形MGK面积的最小值为225平方米. ……………………………………10分
(2)由题意得,
当,解得或(舍去),
由(1)知, ……………………………………14分
即,解之得.
所以的范围是.………………………………………………………16分
20.(1),………………………………………………………………1分
当时,,在上是单调增函数.…………………3分
当时,
由,得,在上是单调增函数;
由,得,在上是单调减函数.
综上,时,的单调增区间是.
时,的单调增区间是,单调减区间是.…6分
(2)由(1)知,当,时,最小,即,
由方程只有一解,得,又考虑到,
所以,解得.…………………………………………………10分
(3)当时,恒成立,
即得恒成立,即得恒成立,
令(),即当时,恒成立.
又,且,当时等号成立.
………………………………………………………………………………………12分
①当时,,
所以在上是增函数,故恒成立.
②当时,若,,
若,,
所以在上是增函数,故恒成立.…………………14分
③当时,方程的正根为,
此时,若,则,故在该区间为减函数.
所以,时,,与时,恒成立矛盾.
综上,满足条件的的取值范围是.……………………………………16分
2011届高三第一次调研考试数学命题意图与讲评建议
各位老师:
此次数学命题是全部高中学数学学习内容,在学校做教师时,我也不赞同全部考查,认为未复习考什么,考查当学意义比较在,但近几年的认识有所转变。未复习考查的是最基本的基础知识、基本方法、基本思想、基本经验,是学生在头脑中留下最本源东西。大家知道,高考必定有些内容是高三复习不到的内容,所以我个人已接受此时考试的价值。对于附加题主要是出于两个方面考虑,一是高二刚学习过的内容,学生忘的不多,且高二时又没有统考,另一方面是附加题部分很多学校都在平时顺带复习的,既然是考试总有学生看一看,考后老师讲一讲,所以附加题考虑再三还是坚持考查。但由于学生并未复习多少内容,理科主要是复习函数、导数、三角函数,三角函数复习也不多,所以命题内容侧重一点函数内容,相对公平,如最后两题都是函数与导数内容,填空题中也考查了三道函数题,第一题考了解三角形。其它内容重在基础知识、基本方法、基本思想的考查,没有涉及到解题技巧,注重考查数学的本质,同时对数学运算量也作了控制,从命之初到打磨成题,对运算量一降再降,但从高考角度,运算总是回避不了的,所以运算能力也许依法是学生首先要解决的问题,没有运算能力数学考试无从谈起。有些试题现在的成题,与当初命思想已有很大差别,现从命题的设想及试题演变角度思考,给出试题讲评建议(仅是个人考虑),供大家讲评时参考,不当之处,请批评。
1.若复数,,其中i是虚数单位,则复数的虚部是 ▲ .
讲评建议:求解过程,体现复数的虚部形成过程,抓住解决问题的本质思维,因此并不需要全部乘开,引导学生做题,小题也要体现思维的简捷性,当然,两复数相除,积模,模积,其模大小,几何意义,若能涉及也要涉及,扩大试题的功能,到复习复数时可以节省时间,复习本身就是一个整合的过程,是一个联系过程,需将每一个知识点放在整个高中数学体系中思考,思考其可能出现情况。
2.已知集合,,若,则实数a的取值范围是 ▲ .
讲评建议:此题当初是求自然数a的范围,但又怕学生不注意“自然数”出错,背离考查集合交集概念的初衷,所以改成求实数a的取值范围。一种集合是区间形式,一种是集合形式,一种是连续,一种是有限三个数,放在一起有的学生可能不习惯。
变式思考,改成,求其范围,又增加难度,但更有意思。
3.若函数为奇函数,则实数 ▲ .
讲评建议:函数是奇函数,且在有意义,即有,很多同学都知道,讲评中要反复强调函数在一定要有意义,且要讲解“,若函数为奇函数,求”,同时考虑讲解“”。此题对我们教学冲击很大,也说明教学研究是无此境的,教师教学要加强研究,不能停留在原有思维层次上,要研究方法不可用情况,特殊情况,越是定势思维,越要注意进行全面研究。2009年南通考了一题用出问题的,大家不妨查一下,对照讲解。
4.若抛物线的焦点坐标为,则抛物线的标准方程
是 ▲ .
5.从某项综合能力测试中抽取10人的成绩,统计如
下表,则这10人成绩的方差为 ▲ .
分数
5
4
3
2
1
人数
3
1
1
3
2
6.如图是一个算法的流程图,则最后输出的 ▲ .
7.已知直线:,:,若∥,则实数a的值是 ▲ .
讲评建议:教材课后有结论,对应成比例,先求后证,这与向量的平行垂直是一致的,联系讲解,让学生构成统一系统,易于应用时调取,容于易混时比较。
8.一个质地均匀的正四面体(侧棱长与底面边长相等的正三棱锥)玩具的四个面上分别标有1,2,3,4这四个数字.若连续两次抛掷这个玩具,则两次向下的面上的数字之积为偶数的概率是 ▲ .
9.已知,,则 ▲ .
讲评建议:此题重在变角公式的应用,当然很简单,这也是学生必须学会的解题技巧,三角函数变换要求在新课标中已有很大的降低,但这样的要注还是需的,若对已知展开用方程思想求解,也应是好方法,也要给予鼓励,从方程角度思考,问题就是解个方程,在差的学生也能会,也许这就是通法。考试时学生可能首先想到的就是“笨”方法,巧方法在那样紧张的环境下很难想出来。
10.已知函数及其导函数的图象如图所示,
则曲线在点P处的切线方程是 ▲ .
讲评建议:此题也体现着解决问题的本质思想,求一个函数在某点处
的切线方程的关键是什么,当然是某点的坐标及此点的导数值,有了
这样的分析此题就太简单了,也许这就是高考想要的思相方法。此题
可能出现的问题是由于导函数是一次函数,原函数是二次函数,学生
会求两个函数,再求切线方程,既走了回路。放在第10题也正是这种用意。
11.在△ABC中,点M满足,若 ,则实数m的值为 ▲ .
讲评建议:一种思维是对已知向量向目标向量分解,一种思维是理解已知向量条件的几何意义,既点M是三角形ABC的重心,再结合,三角形向量的中线形式,此问题观察即可解决,所以掌握相关结论,有了结论便利于联想。
12.设m,n是两条不同的直线,,,是三个不同的平面,给出下列命题:
①若,,则;
②若,,则;
③若,,则;
④若,,,则.
上面命题中,真命题的序号是 ▲ (写出所有真命题的序号)..w.w.k.s
13.若关于x的不等式的解集中的整数恰有2个,则实数a的取值范围 是 ▲ .
讲评建议:解决此题最好的方法是观察,故对条件两边开方,化为,再转化为函数数形结合解决,当然其它的方法也还是有的,教学中有必要展示学生解法,以体现学生的创造性。绝对值函数教学中要引起重视,绝对值函数即是分段函数。从二次函数角度也可以解决,主要是让学生了解决抛物线开口大小的是二次项系数绝对值的大小。若硬解二次不等式,会者也可解之,或直接解一次不等式,等等。
14.已知数列,满足,,,且对任意的正整数,当时,都有,则的值是 ▲ .
讲评建议:遇到这样一个新问题,学生首先应是先去归纳,找规律,这就是一种数学意识,解题意识,教学中要注意培养,如什么时候类比,什么时候归纳。
二、解答题:本大题共6小题,共计90分.请在答题卡指定位置内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
如图,在△ABC中,已知,,,是平分线.
(1)求证:;
(2)求的值.
讲评建议:此题第一问题是关于角平分线性质定理内容,但又是正弦定理的下接应用,考查时主要考虑到学生只有及少数知道角平分线,但教材没有给出角平分线定理,而且用平面几何知识证明,也不容易,题目中也没提及角平分线,主要是让大家重视教材中的例习题,(2)要注重两向量的夹角问题,这常是学生易犯的错误,借此引起学生的重视。当初命制此题是已知,且知的值,第一求,第二求,第三求,这样再求时,除直接用余弦定理求夹角,还可以考虑用向量分解方法求解,而且运算比较简单,但第二问运算量又太大了,为了让学生尽可能得分,所以改成考试试题形式。因此此题求解给教师的教学留出了较大空间,希望各位教师尽时挖掘。
(刚才学生考试,我恰好看了一下,当初怕学生第一题做不好,果然很多学生不会,教师反映,复习只用教辅,不用课本,书上的题不讲,教学必将走入误区,借此因起教师的高度重视,教学复习要教给学生什么,而不仅仅是做题。)
16.(本小题满分14分)
如图,在四棱锥中,四边形是菱形,,且E,F分别是BC, CD的中点. 求证:
(1)EF∥平面;
(2)平面⊥平面.
讲评建议:此题当初是如图情景,最后主要是考虑辅助线太多,
而且两问题之间辅助线滑有联系,同时考虑第二问题难度较大,
所以改成现在形式,希望各位教师讲评时还原本题的原来面目,
同时对第二问题要给予高度重视,主要平面几何的转化思想,
但对高一的求高复习中也要重视,高是教材中要求的。
17.(本小题满分14分)
在各项均为正数的等比数列中,已知,且,,成等差数列.
(1)求数列的通项公式;
(2)设,求数列的前n项和.
此题当初是:是考查学生最基础知识。当初是改变数字,求的前项的和。但考虑到分类讨论,可能比现在还繁,故改为现在情况,重点考查,等差数列、等比数列的基础知识。
18.(本小题满分16分)
已知椭圆E:的左焦点为F,左准线与x轴的交点是圆C的圆心,圆C恰好经过坐标原点O,设G是圆C上任意一点.
(1)求圆C的方程;
(2)若直线FG与直线交于点T,且G为线段FT的中点,求直线FG被圆C所截得的弦长;
(3)在平面上是否存在定点P,使得?若存在,求出点P坐标;若不存在,请说明理由.
讲评建议:对于第二问题当初是仿照2004年江苏高考题命制,用,考查两解情况,后改为,但综合全题还是有一线教师认为运算量较大,后改为现在情况,改成中点后,命题思想完全发生了变化,改成中点,学生用中点坐标公式,是代数方法,而原来思维是方程思想,这一点引起各位注意,对于第三问,也是教材的习题,逆向思维,同时是对两个参量求最值,学生一般接触较少,当然此题也可转化成一个参数,即对平方法,两次用圆方程消元,达到目的,建议教师讲解。同时注意到,此圆是以椭圆的左准线的与x轴的交点为圆心,两个定点恰是椭圆的左右焦点,三问题之间非常和谐,融为一体。
19.(本小题满分16分)
如图1,OA,OB是某地一个湖泊的两条垂直的湖堤,线段CD和曲线EF分别是湖泊中的一条栈桥和防波堤.为观光旅游需要,拟过栈桥CD上某点分别修建与OA,OB平行的栈桥MG,MK,且以MG,MK为边建一个跨越水面的三角形观光平台MGK.建立如图2所示的直角坐标系,测得CD的方程是,曲线EF的方程是,设点的坐标为.(题中所涉及长度单位均为米,栈桥及防波堤都不计宽度)
(1)求三角形观光平台MGK面积的最小值;
(2)若要使的面积不小于320平方米,求的范围.
讲评建议:此题当初(1)是求的最小值,
但两问题过于孤单,且不好设问题,另外量太大了,
两个模型。后只保留现在的(1),但作为倒数第二题,
份量又轻了,最后设计成现在的形式。
对于(2)可以解两次不等式,也可以利用(1)中的单调性,
解一次方程,解一次不等式,建议大家解一次方程,解一次不等式,
因为(1)中提供条件、得出的结论要考虑(2)是否需要。
讲评中求的最小值最好加上去。
20.(本小题满分16分)
已知函数(,且a为常数).
(1)求函数的单调区间;
(2)当时,若方程只有一解,求a的值;
(3)若对所有都有,求a的取值范围.
讲评建议:此题当初是(1)只有一解,求a的范围,大家感觉,作为(1)起点太高,学生不易得分,且上来讨论,又两问题都求范围可以,但还是单调形式单调,后改为现在形式。对于(3)主要是想改变教学中老师不研究情况,分参法是解决参数的一种好方法,但不唯一,且有时其方法不好图象快,如在区间是恒小于,用图象法就很快,同时也要注意到解决参数问题还有很多求不出最值问题。如本题,分参后求不出函数的最值,而且很多参数的范围是求不出来的,是对关键点进行分类讨论求得的。
