高中数学课件新人教a版必修三:分类计数原理与分步计数原理(补充)
文档属性
| 名称 | 高中数学课件新人教a版必修三:分类计数原理与分步计数原理(补充) |

|
|
| 格式 | rar | ||
| 文件大小 | 115.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-12-25 00:00:00 | ||
图片预览







文档简介
课件42张PPT。分类计数原理
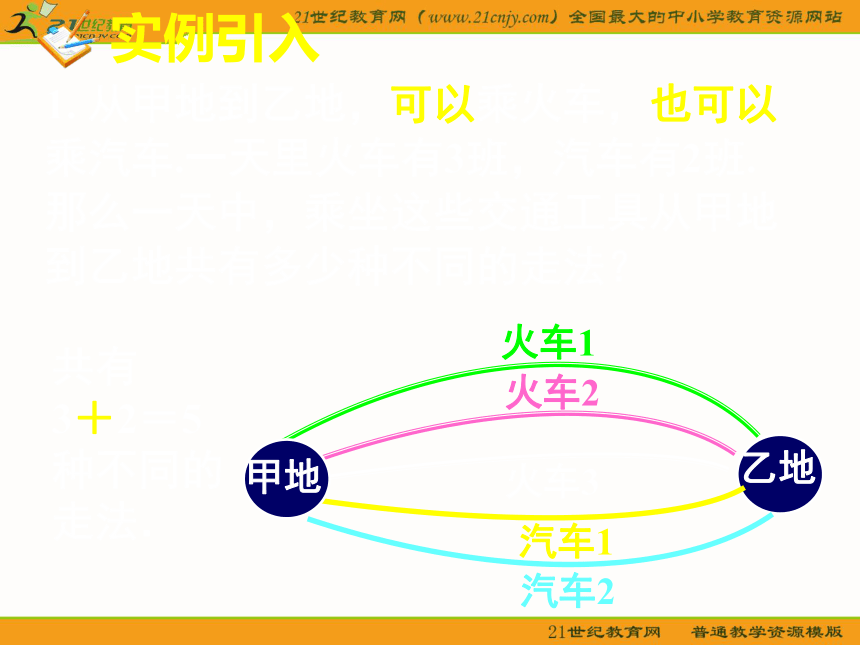
与分步计数原理主讲教师:实例引入1. 从甲地到乙地,可以乘火车,也可以
乘汽车.一天里火车有3班,汽车有2班.
那么一天中,乘坐这些交通工具从甲地
到乙地共有多少种不同的走法?乙地实例引入1. 从甲地到乙地,可以乘火车,也可以
乘汽车.一天里火车有3班,汽车有2班.
那么一天中,乘坐这些交通工具从甲地
到乙地共有多少种不同的走法?共有
3+2=5
种不同的
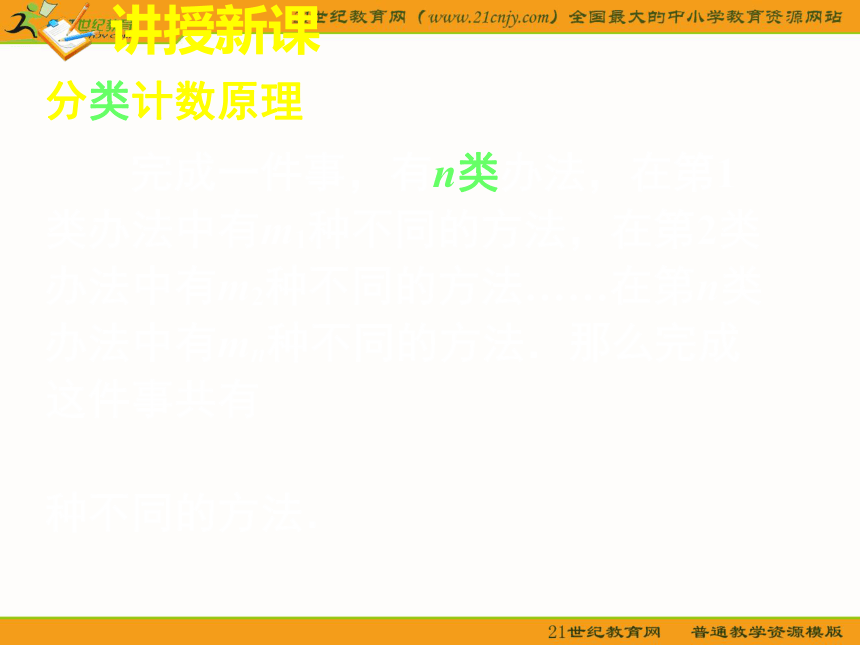
走法.讲授新课分类计数原理 完成一件事,有n类办法,在第1
类办法中有m1种不同的方法,在第2类
办法中有m2种不同的方法……在第n类
办法中有mn种不同的方法.那么完成
这件事共有
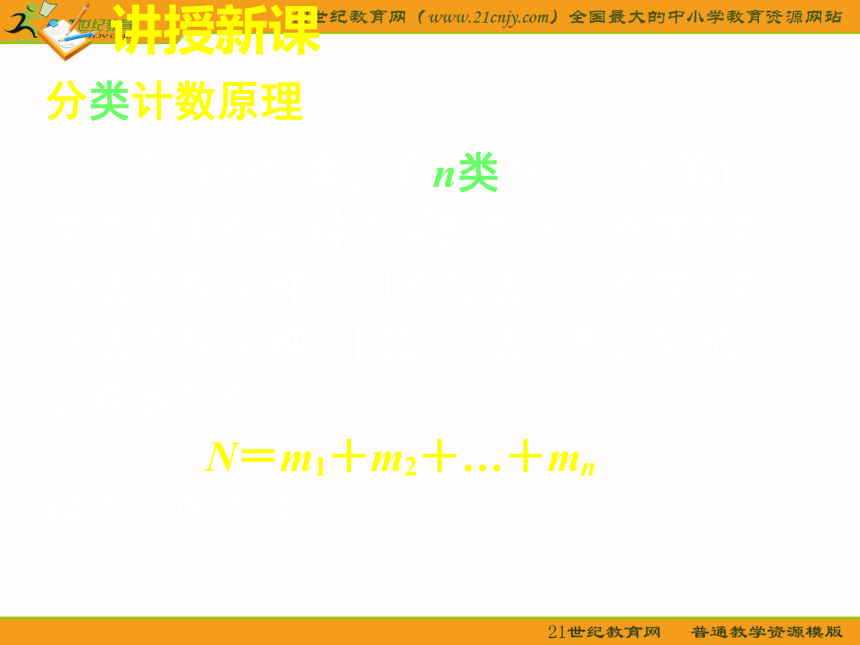
种不同的方法.讲授新课分类计数原理 完成一件事,有n类办法,在第1
类办法中有m1种不同的方法,在第2类
办法中有m2种不同的方法……在第n类
办法中有mn种不同的方法.那么完成
这件事共有
N=m1+m2+…+mn
种不同的方法.对于分类计数原理,注意以下几点:讲授新课⑴从分类计数原理中可以看出,各类之间相
互独立,都能完成这件事,且各类方法数相
加,所以分类计数原理又称加法原理;对于分类计数原理,注意以下几点:讲授新课⑵分类时,首先要根据问题的特点确定一个
分类的标准,然后在确定的分类标准下进行
分类;⑴从分类计数原理中可以看出,各类之间相
互独立,都能完成这件事,且各类方法数相
加,所以分类计数原理又称加法原理;对于分类计数原理,注意以下几点:讲授新课⑵分类时,首先要根据问题的特点确定一个
分类的标准,然后在确定的分类标准下进行
分类;⑶完成这件事的任何一种方法必属于某一类,
并且分别属于不同两类的两种方法都是不同
的方法.⑴从分类计数原理中可以看出,各类之间相
互独立,都能完成这件事,且各类方法数相
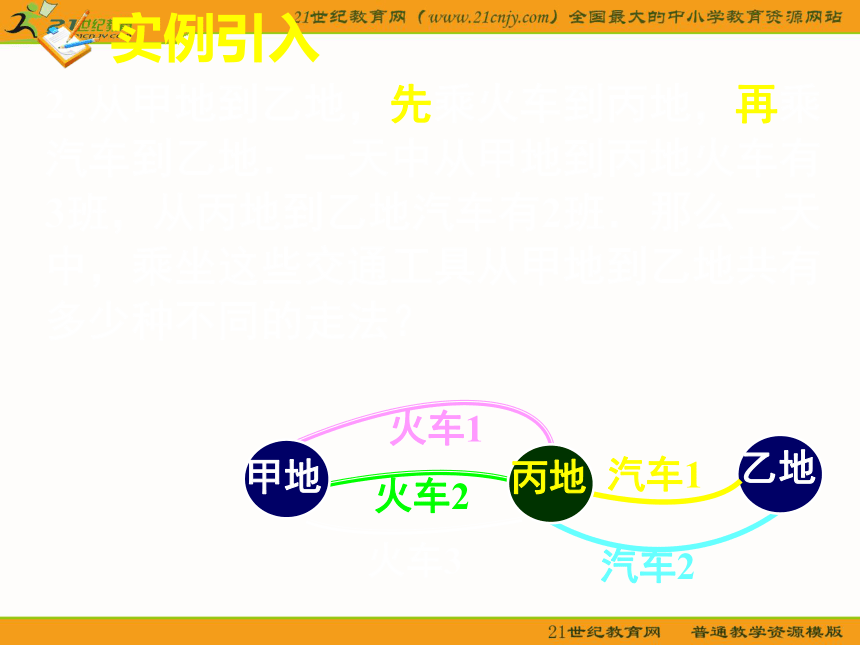
加,所以分类计数原理又称加法原理;对于分类计数原理,注意以下几点:讲授新课2. 从甲地到乙地,先乘火车到丙地,再乘
汽车到乙地.一天中从甲地到丙地火车有
3班,从丙地到乙地汽车有2班.那么一天
中,乘坐这些交通工具从甲地到乙地共有
多少种不同的走法?实例引入甲地乙地2. 从甲地到乙地,先乘火车到丙地,再乘
汽车到乙地.一天中从甲地到丙地火车有
3班,从丙地到乙地汽车有2班.那么一天
中,乘坐这些交通工具从甲地到乙地共有
多少种不同的走法?实例引入甲地火车1火车2火车3汽车1汽车2丙地乙地2. 从甲地到乙地,先乘火车到丙地,再乘
汽车到乙地.一天中从甲地到丙地火车有
3班,从丙地到乙地汽车有2班.那么一天
中,乘坐这些交通工具从甲地到乙地共有
多少种不同的走法?共有
3×2=6
种不同的
走法.实例引入甲地火车1火车2火车3汽车1汽车2丙地乙地分步计数原理 完成一件事,需要分成n个步骤,
做第1步有m1种不同的方法,做第2步
有m2种不同的方法……做第n步有mn
种不同的方法.那么完成这件事共有
种不同的方法.讲授新课分步计数原理 完成一件事,需要分成n个步骤,
做第1步有m1种不同的方法,做第2步
有m2种不同的方法……做第n步有mn
种不同的方法.那么完成这件事共有
N=m1×m2×…×mn
种不同的方法.讲授新课对于分步计数原理,注意以下几点:讲授新课对于分步计数原理,注意以下几点:讲授新课对于分步计数原理,注意以下几点:⑵分步时首先要根据问题的特点确定一个
分步的标准;讲授新课对于分步计数原理,注意以下几点:⑶分步时还要注意满足完成一件事必须并
且只需连续完成 n 个步骤后这件事才算完
成.⑵分步时首先要根据问题的特点确定一个
分步的标准;讲授新课两个原理的相同之处:讲授新课两个原理的相同之处:⑴目的相同:都要“做一件事并完成它”讲授新课两个原理的相同之处:⑴目的相同:都要“做一件事并完成它”⑵所问相同:即问“共有几种不同方法”讲授新课两个原理的相同之处:⑴目的相同:都要“做一件事并完成它”⑵所问相同:即问“共有几种不同方法”两个原理的不同之处:讲授新课两个原理的相同之处:⑴目的相同:都要“做一件事并完成它”⑵所问相同:即问“共有几种不同方法” 分类计数用于分类,各类间独立、
互斥.各类中任何一种方法都能够独
立完成这件事.两个原理的不同之处:讲授新课两个原理的相同之处:⑴目的相同:都要“做一件事并完成它”⑵所问相同:即问“共有几种不同方法” 分类计数用于分类,各类间独立、
互斥.各类中任何一种方法都能够独
立完成这件事. 分步计数原理用于分步,步步相扣,
缺一不可,只有各个步骤都完成了,才
算完成这件事.两个原理的不同之处:讲授新课例1 书架的第1层放有4本不同的计算机书,
第2层放有3本不同的文艺书,第三层放有
2本不同的体育书.
⑴从书架上任取1本书,有多少种不同的
取法?
⑵从书架的第1、2、3层各取1本书,有多
少种不同的取法?讲授新课例1 书架的第1层放有4本不同的计算机书,
第2层放有3本不同的文艺书,第三层放有
2本不同的体育书.
⑴从书架上任取1本书,有多少种不同的
取法?
⑵从书架的第1、2、3层各取1本书,有多
少种不同的取法?(分类计数原理) 讲授新课例1 书架的第1层放有4本不同的计算机书,
第2层放有3本不同的文艺书,第三层放有
2本不同的体育书.
⑴从书架上任取1本书,有多少种不同的
取法?
⑵从书架的第1、2、3层各取1本书,有多
少种不同的取法?(分类计数原理) (分步计数原理) 讲授新课例1 书架的第1层放有4本不同的计算机书,
第2层放有3本不同的文艺书,第三层放有
2本不同的体育书.
⑴从书架上任取1本书,有多少种不同的
取法?
⑵从书架的第1、2、3层各取1本书,有多
少种不同的取法?⑴解:N=m1+m2+m3=4+3+2=9.(分类计数原理) (分步计数原理) 讲授新课例1 书架的第1层放有4本不同的计算机书,
第2层放有3本不同的文艺书,第三层放有
2本不同的体育书.
⑴从书架上任取1本书,有多少种不同的
取法?
⑵从书架的第1、2、3层各取1本书,有多
少种不同的取法?⑴解:N=m1+m2+m3=4+3+2=9.⑵N=m1×m2×m3=4×3×2=24.(分类计数原理) (分步计数原理) 讲授新课⑴一件工作可以用2种方法完成,有5人会用第1种方法完成,另有4人会用第2种方法完成,从中选出1人来完成这件工作,不同选法的种数是有 .课堂练习1.填空:⑵从A村去B村的道路有3条,从B村去C村
的道路有2条,从A村经B村去C村,不同走
法的种数是 .讲授新课⑴一件工作可以用2种方法完成,有5人会用第1种方法完成,另有4人会用第2种方法完成,从中选出1人来完成这件工作,不同选法的种数是有 .1.填空:9 种⑵从A村去B村的道路有3条,从B村去C村
的道路有2条,从A村经B村去C村,不同走
法的种数是 .讲授新课课堂练习⑴一件工作可以用2种方法完成,有5人会用第1种方法完成,另有4人会用第2种方法完成,从中选出1人来完成这件工作,不同选法的种数是有 .1.填空:9 种(分类计数原理) 5+4=9⑵从A村去B村的道路有3条,从B村去C村
的道路有2条,从A村经B村去C村,不同走
法的种数是 .讲授新课课堂练习⑴一件工作可以用2种方法完成,有5人会用第1种方法完成,另有4人会用第2种方法完成,从中选出1人来完成这件工作,不同选法的种数是有 .1.填空:9 种(分类计数原理) 5+4=9⑵从A村去B村的道路有3条,从B村去C村
的道路有2条,从A村经B村去C村,不同走
法的种数是 .6 种讲授新课课堂练习⑴一件工作可以用2种方法完成,有5人会用第1种方法完成,另有4人会用第2种方法完成,从中选出1人来完成这件工作,不同选法的种数是有 .1.填空:9 种(分类计数原理) 5+4=9⑵从A村去B村的道路有3条,从B村去C村
的道路有2条,从A村经B村去C村,不同走
法的种数是 .6 种(分步计数原理) 3×2=6讲授新课课堂练习2.现有高中一年级的学生3名,高中二
年级的学生5名,高中三年级的学生4名.
⑴从中任选1人参加接待外宾的活动,有
多少种不同的选法?
⑵从三个年级的学生中各选1人参加外宾
的活动,有多少种不同的选法?讲授新课课堂练习例2 一种号码锁有4个拨号盘,每个拨号盘
上有从0到9这10个数字,这4个拨号盘可以
组成多少个四位数字号码?讲授新课讲授新课课堂练习3.一城市的某电话局管辖范围内的电话
号码由八位数字组成,其中前四位数字
是统一的,后四位数字都是0到9之间的
一个数字,那么不同的电话号码最多有
多少个?讲授新课例3 要从甲、乙、丙3名工人中选出2名分
别上日班和晚班,有多少种不同的选法? 讲授新课课堂练习4.从5位同学中产生1名组长、1名副组
长,有多少种不同的选法?课堂小结1. 分类计数原理;课堂小结1. 分类计数原理;2. 分步计数原理.课后作业《习案》三十六.
与分步计数原理主讲教师:实例引入1. 从甲地到乙地,可以乘火车,也可以
乘汽车.一天里火车有3班,汽车有2班.
那么一天中,乘坐这些交通工具从甲地
到乙地共有多少种不同的走法?乙地实例引入1. 从甲地到乙地,可以乘火车,也可以
乘汽车.一天里火车有3班,汽车有2班.
那么一天中,乘坐这些交通工具从甲地
到乙地共有多少种不同的走法?共有
3+2=5
种不同的
走法.讲授新课分类计数原理 完成一件事,有n类办法,在第1
类办法中有m1种不同的方法,在第2类
办法中有m2种不同的方法……在第n类
办法中有mn种不同的方法.那么完成
这件事共有
种不同的方法.讲授新课分类计数原理 完成一件事,有n类办法,在第1
类办法中有m1种不同的方法,在第2类
办法中有m2种不同的方法……在第n类
办法中有mn种不同的方法.那么完成
这件事共有
N=m1+m2+…+mn
种不同的方法.对于分类计数原理,注意以下几点:讲授新课⑴从分类计数原理中可以看出,各类之间相
互独立,都能完成这件事,且各类方法数相
加,所以分类计数原理又称加法原理;对于分类计数原理,注意以下几点:讲授新课⑵分类时,首先要根据问题的特点确定一个
分类的标准,然后在确定的分类标准下进行
分类;⑴从分类计数原理中可以看出,各类之间相
互独立,都能完成这件事,且各类方法数相
加,所以分类计数原理又称加法原理;对于分类计数原理,注意以下几点:讲授新课⑵分类时,首先要根据问题的特点确定一个
分类的标准,然后在确定的分类标准下进行
分类;⑶完成这件事的任何一种方法必属于某一类,
并且分别属于不同两类的两种方法都是不同
的方法.⑴从分类计数原理中可以看出,各类之间相
互独立,都能完成这件事,且各类方法数相
加,所以分类计数原理又称加法原理;对于分类计数原理,注意以下几点:讲授新课2. 从甲地到乙地,先乘火车到丙地,再乘
汽车到乙地.一天中从甲地到丙地火车有
3班,从丙地到乙地汽车有2班.那么一天
中,乘坐这些交通工具从甲地到乙地共有
多少种不同的走法?实例引入甲地乙地2. 从甲地到乙地,先乘火车到丙地,再乘
汽车到乙地.一天中从甲地到丙地火车有
3班,从丙地到乙地汽车有2班.那么一天
中,乘坐这些交通工具从甲地到乙地共有
多少种不同的走法?实例引入甲地火车1火车2火车3汽车1汽车2丙地乙地2. 从甲地到乙地,先乘火车到丙地,再乘
汽车到乙地.一天中从甲地到丙地火车有
3班,从丙地到乙地汽车有2班.那么一天
中,乘坐这些交通工具从甲地到乙地共有
多少种不同的走法?共有
3×2=6
种不同的
走法.实例引入甲地火车1火车2火车3汽车1汽车2丙地乙地分步计数原理 完成一件事,需要分成n个步骤,
做第1步有m1种不同的方法,做第2步
有m2种不同的方法……做第n步有mn
种不同的方法.那么完成这件事共有
种不同的方法.讲授新课分步计数原理 完成一件事,需要分成n个步骤,
做第1步有m1种不同的方法,做第2步
有m2种不同的方法……做第n步有mn
种不同的方法.那么完成这件事共有
N=m1×m2×…×mn
种不同的方法.讲授新课对于分步计数原理,注意以下几点:讲授新课对于分步计数原理,注意以下几点:讲授新课对于分步计数原理,注意以下几点:⑵分步时首先要根据问题的特点确定一个
分步的标准;讲授新课对于分步计数原理,注意以下几点:⑶分步时还要注意满足完成一件事必须并
且只需连续完成 n 个步骤后这件事才算完
成.⑵分步时首先要根据问题的特点确定一个
分步的标准;讲授新课两个原理的相同之处:讲授新课两个原理的相同之处:⑴目的相同:都要“做一件事并完成它”讲授新课两个原理的相同之处:⑴目的相同:都要“做一件事并完成它”⑵所问相同:即问“共有几种不同方法”讲授新课两个原理的相同之处:⑴目的相同:都要“做一件事并完成它”⑵所问相同:即问“共有几种不同方法”两个原理的不同之处:讲授新课两个原理的相同之处:⑴目的相同:都要“做一件事并完成它”⑵所问相同:即问“共有几种不同方法” 分类计数用于分类,各类间独立、
互斥.各类中任何一种方法都能够独
立完成这件事.两个原理的不同之处:讲授新课两个原理的相同之处:⑴目的相同:都要“做一件事并完成它”⑵所问相同:即问“共有几种不同方法” 分类计数用于分类,各类间独立、
互斥.各类中任何一种方法都能够独
立完成这件事. 分步计数原理用于分步,步步相扣,
缺一不可,只有各个步骤都完成了,才
算完成这件事.两个原理的不同之处:讲授新课例1 书架的第1层放有4本不同的计算机书,
第2层放有3本不同的文艺书,第三层放有
2本不同的体育书.
⑴从书架上任取1本书,有多少种不同的
取法?
⑵从书架的第1、2、3层各取1本书,有多
少种不同的取法?讲授新课例1 书架的第1层放有4本不同的计算机书,
第2层放有3本不同的文艺书,第三层放有
2本不同的体育书.
⑴从书架上任取1本书,有多少种不同的
取法?
⑵从书架的第1、2、3层各取1本书,有多
少种不同的取法?(分类计数原理) 讲授新课例1 书架的第1层放有4本不同的计算机书,
第2层放有3本不同的文艺书,第三层放有
2本不同的体育书.
⑴从书架上任取1本书,有多少种不同的
取法?
⑵从书架的第1、2、3层各取1本书,有多
少种不同的取法?(分类计数原理) (分步计数原理) 讲授新课例1 书架的第1层放有4本不同的计算机书,
第2层放有3本不同的文艺书,第三层放有
2本不同的体育书.
⑴从书架上任取1本书,有多少种不同的
取法?
⑵从书架的第1、2、3层各取1本书,有多
少种不同的取法?⑴解:N=m1+m2+m3=4+3+2=9.(分类计数原理) (分步计数原理) 讲授新课例1 书架的第1层放有4本不同的计算机书,
第2层放有3本不同的文艺书,第三层放有
2本不同的体育书.
⑴从书架上任取1本书,有多少种不同的
取法?
⑵从书架的第1、2、3层各取1本书,有多
少种不同的取法?⑴解:N=m1+m2+m3=4+3+2=9.⑵N=m1×m2×m3=4×3×2=24.(分类计数原理) (分步计数原理) 讲授新课⑴一件工作可以用2种方法完成,有5人会用第1种方法完成,另有4人会用第2种方法完成,从中选出1人来完成这件工作,不同选法的种数是有 .课堂练习1.填空:⑵从A村去B村的道路有3条,从B村去C村
的道路有2条,从A村经B村去C村,不同走
法的种数是 .讲授新课⑴一件工作可以用2种方法完成,有5人会用第1种方法完成,另有4人会用第2种方法完成,从中选出1人来完成这件工作,不同选法的种数是有 .1.填空:9 种⑵从A村去B村的道路有3条,从B村去C村
的道路有2条,从A村经B村去C村,不同走
法的种数是 .讲授新课课堂练习⑴一件工作可以用2种方法完成,有5人会用第1种方法完成,另有4人会用第2种方法完成,从中选出1人来完成这件工作,不同选法的种数是有 .1.填空:9 种(分类计数原理) 5+4=9⑵从A村去B村的道路有3条,从B村去C村
的道路有2条,从A村经B村去C村,不同走
法的种数是 .讲授新课课堂练习⑴一件工作可以用2种方法完成,有5人会用第1种方法完成,另有4人会用第2种方法完成,从中选出1人来完成这件工作,不同选法的种数是有 .1.填空:9 种(分类计数原理) 5+4=9⑵从A村去B村的道路有3条,从B村去C村
的道路有2条,从A村经B村去C村,不同走
法的种数是 .6 种讲授新课课堂练习⑴一件工作可以用2种方法完成,有5人会用第1种方法完成,另有4人会用第2种方法完成,从中选出1人来完成这件工作,不同选法的种数是有 .1.填空:9 种(分类计数原理) 5+4=9⑵从A村去B村的道路有3条,从B村去C村
的道路有2条,从A村经B村去C村,不同走
法的种数是 .6 种(分步计数原理) 3×2=6讲授新课课堂练习2.现有高中一年级的学生3名,高中二
年级的学生5名,高中三年级的学生4名.
⑴从中任选1人参加接待外宾的活动,有
多少种不同的选法?
⑵从三个年级的学生中各选1人参加外宾
的活动,有多少种不同的选法?讲授新课课堂练习例2 一种号码锁有4个拨号盘,每个拨号盘
上有从0到9这10个数字,这4个拨号盘可以
组成多少个四位数字号码?讲授新课讲授新课课堂练习3.一城市的某电话局管辖范围内的电话
号码由八位数字组成,其中前四位数字
是统一的,后四位数字都是0到9之间的
一个数字,那么不同的电话号码最多有
多少个?讲授新课例3 要从甲、乙、丙3名工人中选出2名分
别上日班和晚班,有多少种不同的选法? 讲授新课课堂练习4.从5位同学中产生1名组长、1名副组
长,有多少种不同的选法?课堂小结1. 分类计数原理;课堂小结1. 分类计数原理;2. 分步计数原理.课后作业《习案》三十六.
