人教版七年级数学下册第七章三角形(全章)
文档属性
| 名称 | 人教版七年级数学下册第七章三角形(全章) |

|
|
| 格式 | rar | ||
| 文件大小 | 508.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-12-24 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第7章 三角形 ★ 7.1 与三角形有关的线段
—— 7.1.1 三角形的边(第1课时)
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
学习目标:
结合具体实例,在认识三角形概念及其基本要素的基础上,学会三角形的表示方法,掌握三角形三边之间的关系;通过观察、操作、交流和反思,获得必需的数学知识,发展空间概念,推理能力和有条理的表达能力。
学习重点:
三角形三边关系的探究与归纳
学习难点:
三角形三边关系的应用
学法指导:
在教师的指导下,学生自己探索和归纳学习知识,加深对所学内容的理解,进一步体会数学知识来源于实际生产和生活。
学习过程:
一、创设情景,新知导入:
三角形是常见的几何图形之一,从自然界景观到微型模型,从建筑物到艺术作品,在日常生活中到处都能找到三角形的影子,你能举出这样的一些实例吗?
二、探究学习
问题一:观察下图:
说说看,上面的三种图形是三角形吗?
如图1所示,如果它是三角形,你能用文字叙述出什么是三角形吗?
A
C b
B C
a
(图1)
从三角形的定义中,我们应注意的是:
①三角形是由三条线段组成的。②此三条线段不共线。③此三条线段首尾顺次连接。④三角形是一个平面图形
问题二:如图一,“三角形”可以用符号“ ”表示。记作“ ”,读作“三角形ABC”。
例:说出图2有多少个三角形?并用符号去表示它们。(请根据注意三角形的定义)
P
E
F G
H
Q (图2)
问题三:三角形的形状、大小和位置由它的三个顶点确定。三角形相邻两边的公共端点叫做三角形的顶点。如图1,“三角形ABC” 有 顶点,它们分别是顶点 ,顶点 ,顶点 。
问题四:组成三角形的三条线段叫做三角形的边。如图1,“三角形ABC”有 边,它们分别是线段 ,线段 ,线段 。有时候,三角形的三边我们也可以用a、b、c来表示。一般地,顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作C。
问题五:三角形相邻两边所组成的角叫做三角形的内角,简称三角形的角。如图1,“三角形ABC”有 内角,它们分别是 , , 。
综合练习:如图3
D
①图中有几个三角形,用符号表示这些三角形和各自的边
A
E
②以AB为边的三角形有哪些?
B C
(图3)
③以E为顶点的三角形有哪些? ④以∠D为角的三角形有哪些?
问题六:按照三角形内角的大小,我们可以将三角形分为锐角三角形,直角三角形,钝角三角形。如下图4是 ,如下图5是 ,如下图6是 。
A A A
C
B C B B C
图4 图5 图6
问题七:根据问题六,我们想一想,如果按照边的关系,我们可以将三角形分为 三角形, 三角形, 三角形。如下图7,下图8,下图9分别是什么三角形?
A A A
B C B C B C图7 图8 图9
(图7是 三角形) (图8是 三角形) (图9是 三角形)
在等腰三角形中,相等的两边叫做腰,另一边叫做底,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
等边三角形是特殊的等腰三角形,即底边和腰相等的等腰三角形。
★根据问题七,三角形按边相等关系分类如下:
不等边三角形
底边和腰不相等的等腰三角形
三角形 等腰三角形
等边三角形
问题八:任意画一个三角形,如图10,假设一只小虫从点B出发,沿三角形的边爬到点C,它有几条线路可以选择?各条线路的长一样吗?
A
B C
( 图10 )
对于任意一个△ABC,如果把其中任意两个顶点(例如B、C)看成定点,由“两点的所有连线
中,线段最短”,可以得到:
AB+AC﹥BC A
同样,若把顶点A、C看作定点,可以得到:
AB+BC﹥AC
若把顶点A、B看作定点,可以得到:
BC+AC﹥AB
一般地,我们有: B C
三角形两边之和大于第三边。
问题九:【动手操作】请同学们根据下图11,图12,图13,用直尺量出三个三角形的三边长度,并填入横线上。
A b a b a b
C c
C
(图11) (图12) (图13)
图11: 图12: 图13:
a= a= a=
b= b= b=
c= c= c=
★计算每个三角形的任意两边之差,并与第三边比较,你能得到什么结论
【自我学习】:请同学们看教材P64,看例题,看解题过程,有看不懂的地方向老师提出疑问。
三、盘点收获
本节课我们学习了三角形的概念及基本要素,重点研究了三角形的三边关系。
(1)从三角形三边关系中,我们可知三角形的三边相互制约——任意两边之和大于第三边,且任意两边之差小于第三边。
(2)判断a、b、c三条线段能否组成一个三角形,应注意: a+b>c,b+c>a,a+c>b。三个条件缺一不可。或者是:当a最长,且有b+c﹥a时,就能构成三角形。
四、达标检测
1、下列各组数字表示三条线段,其中可以组成三角形的是( )
A 12、4、6 B 3、4、5 C 4、15、6 D 2、5、7
2、三角形一边是5,一边是13,则第三边的取值范围是( )
A 5﹤x﹤13 B 8﹤x﹤18 C x﹥8 D x﹤18
3、⊿ABC的三边长分别为整数,周长为11,且有一边为4,则这个三角形可能有的最大边长是( )
A 5 B 5 C 6 D 7
4、各边长均为整数,且三边均不相等的三角形的周长小于13,这样的三角形有( )
A 1个 B 2个 C 3个 D 4个
5、三角形两边分别为4和5,第三边为其中一边的2倍,则第三边长为 。
6、三角形的一边是5,另一边是8,周长恰好是5或8的倍数,则第三边长为 。
7、三角形中有两边长为7和2,第三边为奇数,则三角形周长为 。
8、有长为12、7、5、4的四根木棒,用其中三根组成三角形可有几种方法?为什么?
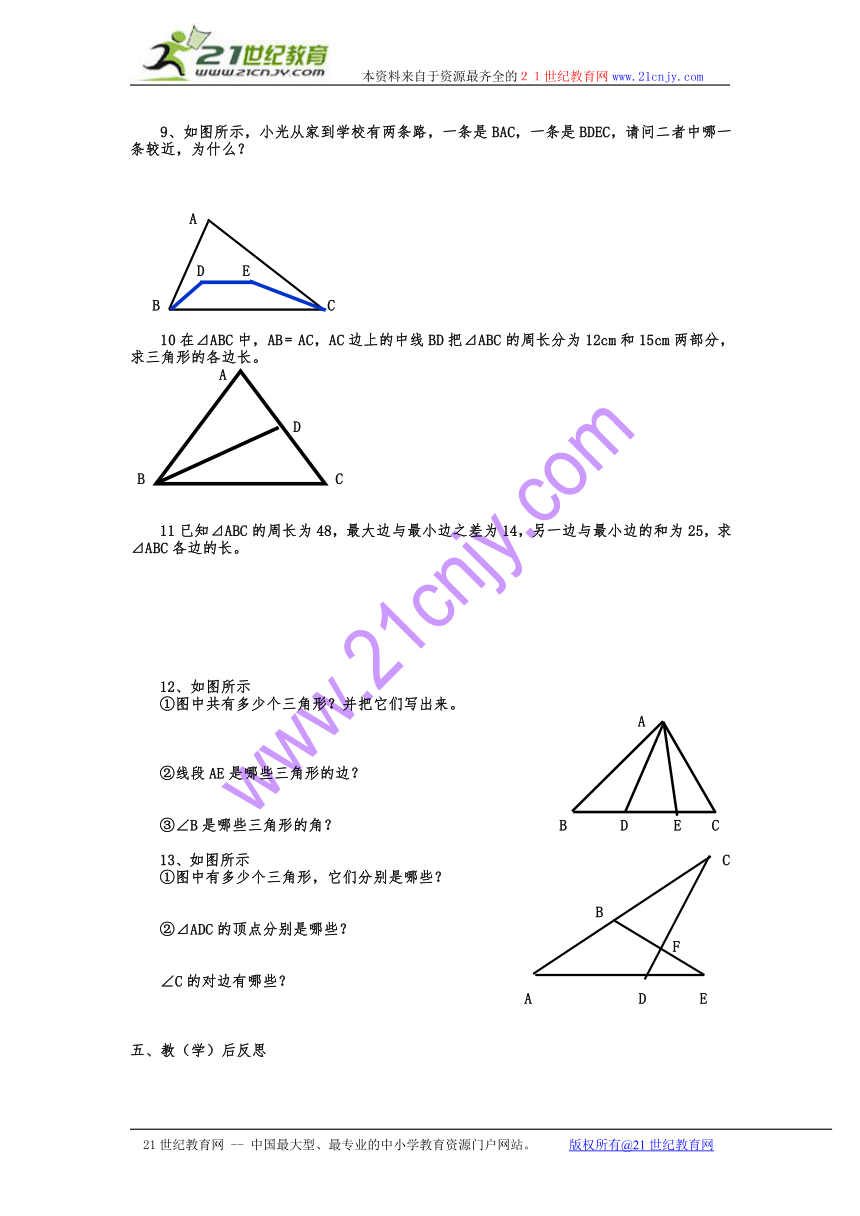
9、如图所示,小光从家到学校有两条路,一条是BAC,一条是BDEC,请问二者中哪一条较近,为什么?
A
D E
B C
10在⊿ABC中,AB﹦AC,AC边上的中线BD把⊿ABC的周长分为12cm和15cm两部分,求三角形的各边长。
A
D
B C
11已知⊿ABC的周长为48,最大边与最小边之差为14,另一边与最小边的和为25,求⊿ABC各边的长。
12、如图所示
①图中共有多少个三角形?并把它们写出来。
A
②线段AE是哪些三角形的边?
③∠B是哪些三角形的角? B D E C
13、如图所示 C
①图中有多少个三角形,它们分别是哪些?
B
②⊿ADC的顶点分别是哪些?
F
∠C的对边有哪些?
A D E
5、教(学)后反思
第7章 三角形 ★ 7.1 与三角形有关的线段
—— 7.1.2 三角形的高、中线与角平分线(第2课时)
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
学习目标:
了解三角形的高、中线与角平分线,并能在具体的三角形中画出它们,通过观察、操作、想象、推理和交流的基础上,发展空间概念,推理能力和有条理的表达能力。
学习重点:
三角形的高、中线与角平分线的概念
学习难点:
准确画出三角形的高、中线与角平分线
学法指导:
在教师的指导下,学生自己探索和归纳学习知识,在动手操作中发现规律,掌握新知
学习过程:
一、创设情景,新知导入:
上一节课,我们认识了三角形及其基本要素:边、角、顶点,请同学们回忆一下,什么样的图形是三角形?三角形三条边之间有什么样的关系?
在前面,我们学习过“过一点画已知直线的垂线”,还能记得它的画法吗?在图一上操作一下 ,并与同桌交流一下自己的画法。 A
·
(图一)
B D C
(图二)
二、探究学习
问题一:从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形这边的高,简称三角形的高。如图二所示。线段AD是BC边上的高。
用同样的方法,你能画出锐角△ABC(图三)的另两条边上的高吗?
注意:标明垂直的记号( )和垂足的字母。 A
如果用折纸的办法能等到它们吗?和同桌进行交流。
观察你的做法,想想这三条高之间有怎样的位置关系?
将你的结果与同桌进行交流。
锐角三角形的三条高 。
再进一步想:锐角三角形的三条高是在三角形的 B C
内部还是在外部? D
锐角三角形的三条高都在 。 (图三)
★ 动手操作:画一个直角三角形。 A
画出直角三角形的三条高,观察它们有怎样的位置关系?
将你的结果与前后同桌进行交流。
直角三角形的三条高 。直角边AC边上的高 是,
直角边BC边上的高 是,斜边AB边上的高 是。 C B
★ 动手操作:画一个钝角三角形。
钝角三角形的三条高交于一点吗?它们所在的直线交于一点吗?将你的结果与同伴进行交流。
A
①钝角三角形的有 高,一条高在三角形的
(内部还是外部),另外的高在三角形的 (内部还是外部)。
②钝角三角形的高交于一点吗? B C
③钝角三角形三条高所在的直线交于一点吗?如果相交于一点,它们相交于钝角三角形的内部还是外部?
归纳:三角形三条高的特性。
锐角三角形 直角三角形 钝角三角形
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三条高所在的直线的交点的位置
问题二:在三角形中,连接一个顶点与它对边的中点的线段,叫做这个三角形的中线。
如图四: A
在图四中,D是BC的中点,线段AD是△ABC的中线。
由定义可知:如果线段AD是△ABC的中线,那么有:
BD=DC=1/2BC
在一个三角形中,有几条中线呢?它们的位置关系又如何呢?请同学们画一画,议一议。(分别画锐角三角形,钝角三角形,直角三角形)
B D C
A (图四) A A
B C B C B C
(锐角三角形) (钝角三角形) (直角三角形)
通过以上作图,我们知道,一个三角形的中线共有 条,它们存在于三角形的 ,并且三角形的三条中线 于一点。我们把这一点叫做重心。
如果通过折纸的方法,能得到它们吗?你是怎么做的,和同伴进行交流。
问题三:在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线。
如图五: A
在图五中,如果AD是∠BAC的角平分线,那么有:
∠BAD=∠DAC=1/2∠BAC
在一个三角形中,有几个角平分线呢?它们的位置关系又如何呢?请同学们画一画,议一议。(分别画锐角三角形,钝角三角形,直角三角形)
B D C
A (图五) A A
(钝角三角形) (直角三角形)
(锐角三角形)
B C B C B C
通过以上作图,我们知道:一个三角形一共有 条角平分线,都在三角形的 ,它们 于一点。我们把这点叫做三角形的内心。
如果通过折纸的方法,能得到它们吗?你是怎么做的,和同伴进行交流。
观察下图,三角形的角平分线与角的平分线有什么区别? A
A
D
B D C B C
结论是: 。
三、盘点收获
本节课,我们主要探究了三角形的高、中线和角平分线。
三角形的高不一定都在三角形的内部:锐角三角形的三条高都在三角形的内部;直角三角形中,有两条高恰好是它的两条直角边;钝角三角形中,两锐角所对边上的高都在三角形的外部。三角形的三条高所在的直线相交于一点。三角形的高是线段。
三角形的中线、角平分线也都是线段;三角形的三条中线、三条角平分线都相交于一点,都在三角形的内部;这一点我们分别称之为重心和内心。
三角形的角平分线与角的平分线既有联系,也有区别,前者是线段,后者是射线。
四、达标检测
1、如图,有一块三角形的土地,需要把其分成4等份给四户农民耕种,只准分成三角形,你有多少种分法?(画出分解图形)
2、如图所示,⊿ABC中,∠BAC是钝角,完成下列作图。 A
①∠BAC的平分线AD
②AC边上的中线BE
B C
③AC边上的高BF
3、如图,若AB⊥CD,垂足是D,则CD是哪些三角形的高?若E是边BC的中点,则AE是哪个三角形的中线?
A
D
B E C
4、若有一条公共边的两个三角形称为一对“共边三角形”,则如图(1)所示中以BC为公共边的“共边三角形”有( ) A 2对 B 3对 C 4对 D 6对
A D
A Ⅱ
E
D Ⅰ O Ⅳ
Ⅲ
B C B C
图(1) 图(2)
5、如图(2)所示,有一个四边形牧场,被对角线分割成4个牧场,若草场中可放4只羊,草场中可放6只羊,草场中可放8只羊,则草场中可放( )
A 10只羊 B 11只羊 C 12只羊 D 13只羊
6、如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是( )
A 锐角三角形 B 钝角三角形 C 直角三角形 D 不能确定
7、关于三角形的三条中线,下列说法中正确的是( )
A 必在三角形的内部 B 必在三角形的外部
C 必和三角形的一条边重合 D 以上皆有可能
8、如下图所示,已知⊿ABC,过点A画一条平分三角形面积的直线。
A
A
D
B C B E C
9、如图所示,D、E分别为⊿ABC的边AC、BC的中点,则下列说法中,不正确的是( )
A DE是⊿BDC的中线 B BD是⊿ABC的中线 C AD﹦DC,BE﹦EC D ∠C的对边是DE
10、在图(3)中,互不重叠的三角形共有4个,在图(4)中,互不重叠的三角形共有7个,在图(5)中,互不重叠的三角形共有10个,……则在第 n个图形中,互不重叠的三角形共有多少个?(用含n的式子表示)
图(3) 图(4) 图(5)
11、如图所示,在⊿ABC中,DE∥BC,EF∥AB,BE平分∠DBF交DF于点O,则EO是否是∠DEF的角平分线?请说明理由。
A
D E
O
B F C
5、教(后)学反思
第7章 三角形 ★ 7.1 与三角形有关的线段
—— 7.1.3 三角形的稳定性(第3课时)
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
学习目标:
通过观察和实际操作得到三角形具有稳定性,四边形没有稳定性的结论;以及三角形稳定性和四边形没有稳定性在生产和生活中的应用
学习重点:
了解三角形稳定性在生产、生活中的实际应用
学习难点:
准确使用三角形稳定性于生活之中
学法指导:
观察、操作、探究、交流
学习过程:
一、创设情景,新知导入:
盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做?
你的理由是:
二、探究学习
问题一:如图一:将三根木条用钉子钉成
一个三角形木架,然后扭动它,它的形状会改
变吗?
(图一)
问题二:如图二,将四根木条用钉子钉成
一个四边形木架,然后扭动它,它的形状会改
变吗?
(图二)
问题三:在四边形木架上再钉一根木条,将
它的一对顶点连接起来,然后扭动它,这时木架
的形状还会改变吗?为什么?
(图三)
通过我们的实际操作,我们发现,三角形木架的形状 (如图一),而四边形的形状 (如图二)。
说明:三角形是具有 的图形,而四边形没有 。
通过图三发现,斜钉一根木条的四边形木架的形状 。这是因为斜钉一根木条后,四边形变成了两个 ,由于三角形具有 ,窗框在未安装好之前也不会变形。
问题四:三角形的稳定性在生活中有广泛的应用,如下图,除外。你能举出相应的例子吗
(屋顶钢架)
问题五:四边形的不稳定性也有广泛的应用,如下图所示,除外,你还能举出其他的实例吗?
三、盘点收获
我们通过操作,了解了三角形具有稳定性,四边形不具有稳定性的特点,也就是说,一个三角形的三条边固定了,三角形的形状和大小就完全确定了。所有的多边形中,只有三角形具有稳定性。
四、达标检测
1下列图形中不具有稳定性的是( )
2撑上支撑后的自行车能稳稳地停在地上,是因为自行车的两个轮胎与地面以及支撑形成了一个三角形,三角形具有( )。
5、教(学)后反思
第7章 三角形 ★ 7.2 与三角形有关的角
—— 7.2.1 三角形的内角(第1课时)
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
学习目标:
1、经历实验活动的过程,得出三角形的内角和定理,能用平行线的性质推出这一定理
2、能应用三角形内角和定理解决一些简单的实际问题
学习重点:
三角形内角和定理
学习难点:
三角形内角和定理的推理过程
课前准备:
每个学生准备好两个由硬纸片剪出的三角形
学法指导:
在教师的指导下,学生自己探索和归纳学习知识,加深对所学内容的理解。
学习过程:
一、创设情景,新知导入:
在前面我们学习了与三角形有关的线段,请同学们回忆一下所学内容,回答如下问题:
①什么是三角形与三角形的表示方法 A
②三角形的主要线段
③三角形三边的关系 B C
二、探究学习
问题一:【动手操作】请同学们任意画一个三角形,并用量角器测量一下,每个内角的度数是多少?三角形三个内角的度数和又是多少?同伴之间交流。
通过我们的操作,我们可以得出结论:
三角形三个内角的和等于 。
问题二:在实际生活中,由于形状不同的三角形有无数个,我们不可能用度量的方法一一验证所有三角形。那么我们该如何求证上面结论的正确性呢?
下面请同学们拿出我们事先准备好的两个硬纸片三角形,并在硬纸片三角形上标出三个内角的编码,按下面图1、图2、图3方式拼合在一起,能得到什么?在这个操作过程中,你能发现证明的思路吗?
(图1) (图2)
想一想,如果我们不用剪,拼办法,可不可以用推理论证的方法来说明上面结论的正确性呢?
★ 操作应用:
已知:△ABC (图4) A
求证:∠A+∠B+∠C=180° E
方法一:
证明:在△ABC的外部以CA为边作
∠ACE=∠A。延长BC至D
∵ ∠ACE=∠A
∴ CE∥BA(内错角相等,两直线平行) B D
∴ ∠DCA=∠B( ) C
∵ ∠BCA+∠ACE+∠ECD=180°(平角定义) (图4)
∴ ∠BCA+∠A+∠B=180°(等量代换)
方法二:(图4)
证明:延长BC至D,过点C作CE∥BA
则∠A=∠ACE( )
∠B=∠ECD ( )
∵ ∠BCA+∠ACE+∠ECD=180°(平角定义
∴ ∠BCA+∠A+∠B=180°(等量代换) A
方法三:(图5) E F
证明:过点A作EF∥BC
则 ∠EAB=∠B ( )
∠FAC=∠C ( )
∵ ∠EAB+∠BAC+∠CAF=180°(平角定义)
∴ ∠B+∠BAC+∠C=180°(等量代换) B C
(图5)
通过以上推导过程,可以看出,证明是由题设(已知)出发,经过一步步的推理,最后推出结论(求证)正确的过程。
★ 例题探讨:
C岛在A岛的北偏东方向,B岛在A岛的北偏东方向,C岛在B岛的北偏西方向,从C岛看A、B两岛的视角是多少度?
分析:A、B、C三岛的连线构成△ABC,所求的∠ACB是△ABC的一个内角。如果能求出∠CAB、∠ABC,就能求出∠ACB。
解:∠CAB=∠BAD-∠CAD=80°-50°=30°
由AD∥BE,可得:
∠BAD+∠ABE=180°( )
所以:
∠ABE=180°-∠BAD=180°-80°=100°
∠ABC=∠ABE-∠EBC=100°-40°=60°
在△ABC中,
∠ACB=180°-∠ABC-∠CAB=180°-60°-30° =90°
答:从C岛看A、B两岛的视角是90°
三、盘点收获
知识要点 总结 注意问题 解题方法总结
三角形内角和定理 三角形的三个内角的和等于180° 此定理应用的前提条件是在同一个三角形中。 (1)已知两角或两角的和,求另一个角,利用三角形内角和定理。
四、达标检测
1、一个三角形最多有 个直角,最多有 个钝角。
2、若一个三角形的三个内角之比为2:3;4,则这三个内角的度数分别是 , , 。
3、在△ABC中,若∠A+∠B=2∠C,则∠C= °。
α
4、如图:∠α= 。 48°
32° 44°
5、在△ABC中,∠A=∠B+∠C,则△ABC是 三角形。
6、在△ABC中,∠C=2(∠A+∠B),则∠C= 。
7、一个三角形的三个内角的度数比是2:3:7,这个三角形是( )
A 直角三角形 B 等腰三角形 C 锐角三角形 D 钝角三角形
8、如图(1)所示,若∠1﹥∠2,则∠1、∠2、∠3用“﹤”连结,正确的是( )
A ∠3﹤∠2﹤∠1 B ∠2﹤∠1﹤∠3 C ∠2﹤∠3﹤∠1 D 以上都不对
A
A D
1
O
2 3
B E
C B C
图(1) 图(2) A
9、如图(2),所示,∠A﹢∠B﹢∠C﹢∠D﹢∠E﹦
1
10、如图(3)所示,∠1、∠2、∠3、∠4满足的关系式是( )
A ∠1﹢∠2﹦∠3﹢∠4 B ∠1﹢∠2﹦∠4-∠3 C
C ∠1﹢∠4﹦∠2﹢∠3 D ∠1﹢∠4﹦∠2-∠3
A E
2
O 4 3 B
图(3)
E
B 2 1 C
图(4)
D
11、 如图(4)所示,下列说法中错误的是( )
A ∠2﹦∠A﹢∠B﹢∠D B ∠1﹦∠2-∠D C ∠2﹦∠A﹢∠D D ∠2﹥∠1﹥∠A
12、如图(5)所示,∠A﹦∠C,CD⊥AB于D,交AE于F,试判定⊿AEB的形状,并说明你的理由。 A
D
F
B C
E
13、如下图(1)所示,在⊿ABC中,AE平分∠BAC(∠C﹥∠B),F为AE上一点,且FD⊥BC于点D。 (1)试推导∠EFD与∠B、∠C之间的大小关系。
(2)如图(2),当点F在AE的延长线上时,其余条件都不变,判断你在(1)中推导的结论是否还成立? A A
F
D
B C B E C
E D
F
五、教(学)后反思
第7章 三角形 ★ 7.2 与三角形有关的角
—— 7.2.2 三角形的外角(第2课时)
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
学习目标:
1、使学生在操作活动中,探索并了解三角形的外角的两条性质
2、利用学过的定理论证这些性质
3、能利用三角形的外角性质解决实际问题
学习重点:
三角形的外角性质;三角形的外角和定理
学习难点:
三角形外角的定义及定理的论证过程
学法指导:
学练结合
学习过程:
一、创设情景,新知导入:
上节课,我们学习了三角形内角和定理,其定理内容是什么?
如下图把的一边BC延长到D,得,它不是三角形的内角,那它是三角形的什么角?
什么是三角形的外角?
二、探究学习
问题一:观察图1,思考: A
①一个三角形有多少个外角? 不相邻
内角 相邻内角
②请根据图1完成下面填空
∠A+∠B+∠1= ( ) 外角
1
∠ACD+∠1= ( )
B C D
③根据上面的填空,我们得出下列关系: (图1)
∠ACD=∠A+∠B 其理由是 。
一般地,有下面的结论:
三角形的一个外角等于与它不相邻的两个内角的和。
由上面的结论,可以得到:
三角形的一个外角大于与它不相邻的任何一个内角。
根据图1,完成选择( ﹥ ﹤ ):①∠ACD ∠A ②∠ACD ∠B
问题2:观察图2给予的提示,求证:∠1+∠2+∠3=360°1 A
已知:
求证:∠1+∠2+∠3=360°
证明:
2
B
3 (图2) C
经过刚才我们的证明,可以得到:三角形的外角和等于 。
除了刚才的证明方法外,我们也可以用下面的方法去证明。根据下图3的提示,想一想,该怎样证明∠1+∠2+∠3=360°,写出你的证明过程。 4
1 D
A
2
B
3 (图3) C
三、盘点收获
知识要点 总结 注意问题 解题方法总结
三角形外角的概念及性质 三角形的一边与另一边的延长线组成的角,叫做三角形的外角。性质1三角形的一个外角等于与它不相邻的两个内角的和。性质2三角形的一个外角大于与它不相邻的任何一个内角。 添加辅助线把问题转化为三角形问题,实现条件的转化。 (2涉及角的不等关系,利用“三角形的一个外角大于与它不相邻的任何一个内角”来解题。
四、达标检测
1、三角形的外角和是指三角形所有外角的和。( )
2、三角形的外角和等于它内角和的2倍。( )
3、三角形的一个外角等于两个内角的和。( )
4、三角形的一个外角等于与它不相邻的两个内角的和。( )
5、三角形的一个外角大于任何一个内角。( )
6、三角形的一个内角小于任何一个与它不相邻的外角。( )
7、三角形的三个外角中最多有 锐角,最多有 个钝角,最多有 个直角。
8、如图4,X=
9、如图5,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连EF, 则∠1,∠2,∠3的大小关系是_________
(图4) (图5)
10、如下图(1),求出∠A+∠B+∠C+∠D+∠E+∠F的度数
11、如上图(2),求出∠A+∠B+∠C+∠D+∠E+∠F的度数
5、教(学)后反思
第7章 三角形 ★ 7.3 多边形及其内角和
—— 7.3.1 多边形(第1课时)
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
学习目标:
了解多边形及有关概念,理解正多边形及其有关概念
学习重点:
了解多边形及其有关概念,理解正多边形及其有关概念
学习难点:
多边形定义的准确理解
学法指导:
自学为主,教师指导
学习过程:
一、创设情景,新知导入:
前面我们学习了三角形,你能说说学习了哪些有关三角形的知识?
①观察图1,你能说出三角形的定义吗?
(图1) (图2)
②观察图2,既然我们已经知道什么叫三角形,
你能根据三角形的定义,说出什么叫四边形吗?
③观察图3,什么叫五边形呢? (图3) (图4)
二、探究学习
问题一:通过上面三角形,四边形,五边形的定义,我们知道了什么是三角形,四边形,五边形。那么多边形的定义又是什么?(图5)
问题二:通过对图1—图4的观察,我们知道:多边形是按组成它的线段的条数而进行分类的,三角形是最基本的多边形。那么什么是多边形的内角?多边形的外角?
对于图2来说,它的内角分别是: 、 、 、 。
对于图3来说,它的内角分别是: 、 、 、 、 。
对于图4来说,它的内角分别是: 、 、 、 、 、 。
因此我们说:多边形相邻两边组成的角叫做它的 。
观察图5,∠1是多边形ABCDE的一个 。
对于图2来说,它的外角有 个,对于图3来说,它的
外角有 个,对于图4来说,它的外角有 个,那么n边形
有 个外角。
(图5)
问题三:根据前面的学习内容,我们说,多边形的内角,边,外角有着一定的关系,请你填写下表,能发现它们之间的规律吗?
多边形的边数 3 4 5 6 7 … n
多边形内角的个数
多边形边的个数
多边形外角的个数
规律是:
问题四:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线。请将下列图形根据多边形对角线的定义,试着连接,从中寻找规律,完成表格的填写。
多边形的边数 3 4 5 6 7 n
从一个顶点引对角线的条数
分成的三角形的个数
规律是:从n边形的一个顶点可以引 条对角线,把多边形分成 个三角形。
问题五:观察图6,画出四边形ABCD的任何一条边,(如AB)所在的直线,整个四边形都在这条直线的同一侧,这样的四边形叫做凸四边形。而图7中的四边形ABCD就不是凸四边形,因为画CD(或BC)所在的直线,整个四边形不都在这条直线的同一侧。
A
D
B
(图6)
C
(图7)
类似地,画多边形的任何一条边所在的直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形。这是我们本节课讨论的内容。
问题六:三角形如果三条边都想的,三个角也都相等,那么这样的三角形就叫做正三角形。如果多边形各条边都相等,各个角也都相等,那么这样的多边形就叫做正多边形。(如下图所示)
(正三角形) (正四边形) (正五边形) (正六边形) (正八边形)
三、盘点收获
在一个平面内,由一些线段首尾顺次连结组成的图形叫做多边形。
各个角都相等,各条边都相等的多边形叫做正多边形。
n边形的对角线等于[n×(n-3)]÷2.
四、达标检测
(一)、判断题.
1.由四条线段首尾顺次相接组成的图形叫四边形.( )
2.由不在一直线上四条线段首尾次顺次相接组成的图形叫四边形.( )
3.由不在一直线上四条线段首尾顺次接组成的图形,且其中任何一条线段所在的直线、使整个图形都在这直线的同一侧,叫做四边形.( )
4.在同一平面内,四条线段首尾顺次连接组成的图形叫四边形.( )
(二)、填空题.
1.连接多边形 的线段,叫做多边形的对角线.
2.多边形的任何 所在的直线,整个多边形都在这条直线的 ,这样的多边形叫凸多边形.
3.各个角 ,各条边 的多边形,叫正多边形.
(三)、解答题.
1.在正四边形ABCD中,你能用四中不同的方法把正四边形的面积四等分吗?
2.如上图(2),O为四边形ABCD内一点,连接OA、OB、OC、OD可以得几个三角形?它与边数有何关系?
3.如上图(3),O在五边形ABCDE的AB上,连接OC、OD、OE,可以得到几个三角形?它与边数有何关系?
4.如上图(4),过A作六边形ABCDEF的对角线,可以得到几个三角形?它与边数有何关系?
五、教(学)后反思
第7章 三角形 ★ 7.3 多边形及其内角和
—— 7.3.2 多边形的内角和(第2课时)
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
学习目标:
1、使学生了解多边形的内角、外角等概念
2、能通过不同方法探索多边形的内角和与外角和公式,并会应用它们进行有关计算
学习重点:
1、多边形的内角和公式
2、多边形的外角和公式
学习难点:
多边形的内角和定理的推导
学法指导:
探究学习
学习过程:
一、创设情景,新知导入:
1我们知道三角形的内角和为180°。
2我们还知道,正方形(正四边形)四个角都等于90°,那么它的内角和为360°,同样,长方形的内角和也是360°。
3正方形和长方形都是特殊的四边形,其内角和为360°。那么,任意一个四边形的内角和是否也是360°呢?
二、探究学习
问题一:请同学们画一个任意四边形,用量角器量出它的四个内角度数,计算它们的和,与同桌进行交流结果。
结论:任意一个四边形的内角和等于 。
我们能利用三角形内角和定理去证明我们得出的这个结论吗?
问题二:根据下面提供的图形和文字,做一做,填一填,找出规律。
A F
D A A
A
D E
B B B B D
C C C C
(图1) (图2) (图3) (图4)
①如图1,三角形ABC的内角和是多少度?( )
②如图2,图中有几个三角形?( )四边形的内角和是多少度?( )
③如图3,图中有几个三角形?( )五边形的内角和是多少度?( )
④如图4,图中有几个三角形?( )六边形的内角和是多少度?( )
多边形的边数 3 4 5 6 7 … n
分成三角形的个数
多边形的内角和
由此,我们得出:n边形的内角和= 。
问题三:要得到多边形的内角和必需通过“三角形内角和定理”来完成,就是把一个多边形分成几个三角形。除利用对角线把多边形分成几个三角形外,还有其他的分法。(以五边形为例)
分法一:观察图5,在五边形ABCDE内取一点O,连接OA、OB、OC、OD、OE,则得五个三角形。其五个三角形的内角和为5×180°,而∠1、∠2、∠3、∠4、∠5(这五个角合在一起变成周角)不是五边形的内角,应减去,所以:五边形的内角和为5×180°-2×180°=(5-2)×180°=540°
(图5)
如果五边形变成n边形,用同样的方法也可以得到n个三角形的内角和减去一个周角,即可得:n边形内角和=n×180°-2×180°=(n-2)×180°。
分法二:观察图6,在五边形的边AB上取一点O,连接OE、OD、OC,则可以得到(5-1)个三角形,而∠1、∠2、∠3、∠4不是五边形的内角,应舍去。
所以:五边形的内角和为(5-1)×180°-180°=(5-2)×180°
用同样的方法,也可以把n边形分成(n-1)个三角形,把不是n边形内角的∠AOB舍去,即可得n边形的内角和为(n-2)×180°
(图6)
问题三:图图7,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和。六边形的外角和等于多少?
(1)任何一个外角同与它相邻的内角有什么关系?
(2)六边形的6个外角加上与它们相邻的内角,所得的总和是多少?
(3)上述总和与六边形的内角和,外角和有什么关系?
(图7)
如果将图7中的六边形换成n边形(n的值是不小于3的任意整数)也可以得到同样的结果吗?
由问题三的探究,我们可以得到:多边形的外角和等于 。
所以我们说,多边形的外角和与它的边数无关。
对此,我们也可以像以下这样理解,为什么多边形的外角和等于360°
如右图,从多边形的一个顶点A出发,沿多边形各边走过
各顶点,再回到A点,然后转向出发时的方向,在行程中所转
的各个角的和就是多边形的外角和,由于走了一周,所得的各
个角的和等于一个周角,所以多边形的外角和等于360
三、盘点收获
知识要点 总结 注意问题 解题方法总结
多边形内角和定理 n边形内角和等于(n-2)×180° 内角和随多边形边数的改变而改变。 (1)常利用对角线将多边形问题转化为三角形问题解决。(2)定值问题长从多边形外角和的方向来考虑。
多边形外角和定理 多边形的内角和等于360° 多边形的外角和是定值。
四、达标检测
(一)、判断题.
1.当多边形边数增加时,它的内角和也随着增加.( )
2.当多边形边数增加时.它的外角和也随着增加.( )
3.三角形的外角和与一多边形的外角和相等.( )
4.从n边形一个顶点出发,可以引出(n一2)条对角线,得到(n一2)个三角形.( )
5.四边形的四个内角至少有一个角不小于直角.( )
(二)、填空题.
1.一个多边形的每一个外角都等于30°,则这个多边形为 边形.
2.一个多边形的每个内角都等于135°,则这个多边形为 边形.
3.内角和等于外角和的多边形是 边形.
4.内角和为1440°的多边形是 .
5.一个多边形的内角的度数从小到大排列时,恰好依次增加相同的度数,其中最小角为100°,最大的是140°,那么这个多边形是 边形.
6.若多边形内角和等于外角和的3倍,则这个多边形是 边形.
7.五边形的对角线有 条,它们内角和为 .
8.一个多边形的内角和为4320°,则它的边数为 .
9.多边形每个内角都相等,内角和为720°,则它的每一个外角为 .
10.四边形的∠A、∠B、∠C、∠D的外角之比为1:2:3:4,那么∠A:∠B:∠C:∠D= .
11.四边形的四个内角中,直角最多有 个,钝角最多有 个, 锐角最多有 个.
12.如果一个多边形的边数增加一条,那么这个多边形的内角和增加 ,外角和增加 .
(三)、选择题.
1.多边形的每个外角与它相邻内角的关系是( )
A.互为余角 B.互为邻补角 C.两个角相等 D.外角大于内角
2.若n边形每个内角都等于150°,那么这个n边形是( )
A.九边形 B.十边形 C.十一边形 D.十二边形
3.一个多边形的内角和为720°,那么这个多边形的对角线条数为( )
A.6条 B.7条 C.8条 D.9条
4.随着多边形的边数n的增加,它的外角和( )
A.增加 B.减小 C.不变 D.不定
5.若多边形的外角和等于内角和的和,它的边数是( )
A.3 B.4 C.5 D.7
6.一个多边形的内角和是1800°,那么这个多边形是( )
A.五边形 B.八边形 C.十边形 D.十二边形
7.一个多边形每个内角为108°,则这个多边形( )
A.四边形 B,五边形 C.六边形 D.七边形
8,一个多边形每个外角都是60°,这个多边形的外角和为( )
A.180° B.360° C.720° D.1080°
9.n边形的n个内角中锐角最多有( )个.
A.1个 B.2个 C.3个 D.4个
10.多边形的内角和为它的外角和的4倍,这个多边形是( )
A.八边形 B.九边形 C.十边形 D,十一边形
11.过多边形的一个顶点可以引9条对角线,那么这个多边形的内角和是( )
A 1620° B 1800° C 1980° D 2160°
12.八边形的对角线的条数是( )
A 9条 B 14条 C 20条 D 24条
13.如果把一个多边形的边数增加1倍,它的内角和是2160°,那么原来多边形的边数是( )
A 5条 B 6条 C 7条 D 8条
14.下面几个结论:①三角形的外角中最多只有一个锐角;②正n边形的内角度数等于180°-360°/n;③多边形的内角和不一定大于多边形的外角和;④n边形的边数每增加1条,对角线就增加 n条;⑤任何一个多边形中,锐角不超过3个。其中正确的有( 0
A 2个 B 3个 C 4个 D 5个
15.如图(1)所示,试求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
D
A G
E F
B C
图(1)
16.★探究题★ 过m边形的一个顶点有7条对角线,n边形没有对角线,k边形共有k条对角线,则(m-K)n为多少?
17.★开放题★ 如图,把正方形截下一个角后,得到的图形的内角和为多少
5、教(学)后反思
第7章 三角形 ★ 7.4 课题学习 镶嵌
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
学习目标:
1、会用正多边形无缝隙、不重叠第覆盖平面
2、让学生应用已有的数学知识和能力,探索和解决镶嵌问题的过程中,感受数学知识的价值,增强应用意识,获得各种体验
学习重点:
会用正多边形无缝隙、不重叠第覆盖平面
学习难点:
哪些多边形形状可以镶嵌平面图形
学法指导:
实际操作,感受体验带来的快乐
学习过程:
一、创设情景,新知导入:
观察提供的图片:
我们经常能看到各种建筑物的地板,观察地板,就能发现地板常用各种正多边形地砖砌成美丽的图案。
二、探究学习
问题一:镶嵌定义。
用一些形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙,不重叠的把平面的一部分完全覆盖,这就是平面图形的镶嵌。
注意:各种图形拼接后既要无缝隙,又不重叠。
利用镶嵌我们可以得到一些绚丽多
彩的图案。
问题二:【动手操作】 请同学们将准备好的图形,如边长相同的正三角形,正方形,正五边形,正六边形等拿出来,按提示要去操作。
(1)用边长相同的正三角形能否镶嵌?结论是:用边长相同的正三角形 镶嵌。
(2)用边长相同的正方形能否镶嵌?结论是:用边长相同的正方形 镶嵌。
(3)用边长相同的正五边形能否镶嵌?结论是:用边长相同的正五边形 镶嵌。
(4)用边长相同的正六边形能否镶嵌?结论是:用边长相同的正六边形 镶嵌。
根据我们刚才的实际操作拼接,想一想,镶嵌平面图案需要什么条件?
条件是:拼接在同一个点的各个角的和恰好等于 。
三、盘点收获
本节我们学习了在平面内如何镶嵌的知识。
知识要点 总结 注意问题 解题方法总结
平面镶嵌的定义 用一些不重叠摆放的多边形把平面的一部分完全覆盖,在几何里叫做平面镶嵌。 平面镶嵌既不能重叠也不能有空隙。 在进行平面镶嵌的图案设计问题中,要使拼接在同一个顶点的各个多边形的内角和等于360°。
平面镶嵌的条件 (1)拼接在同一点的各个角的和恰好等于360°(2)相邻的多边形有公共边,当所用的多边形为正多边形时,它们的边长应相等。 两个条件必须同时满足,缺一不可。
四、达标检测
1、在一个顶点处,若n边形的几个内角的和为 ,则此正n边形可铺满地面,没有空隙。
2、能用一种正多边形进行平面镶嵌的有 、 、
3、能用一种任意多边形进行平面镶嵌的有
4、如果只用圆、正五边形、矩形中的一种图形镶嵌整个平面,那么这个图形只能是
5、只用正三角形和正六边形地板铺地面,你有几种方案?
6、在一间长6m,宽3.5m的客厅地面上,要铺同种规格的正方形地砖,现在有““40cm×40cm”,“30cm×30cm”,“50cm×50cm”,“60cm×60cm”的地砖,请你设计一下,需要全部铺满,不能破地砖,不留一点空隙,也不多余,选哪一种规格,为什么?
7、如图所示,你能将一个正三角形分成8个大小、形状意义的直角三角形吗?若能,请你画出图形。
8、用m个正三角形和n个正六边形铺满地面,先求出m、n的值,再各自设计一种铺法,并作出设计的图形。
5、教(学)后反思
第7章 三角形 复习课
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
复习目标:
通过对本章知识结构图,加深本章知识的理解;
对知识点的归纳,是为了更好地的在解决本章知识的时候,能灵活运用。
复习过程:
一、三角形知识结构图:
三角形的边
与三角形 高线
有关的线段 中线
角平分线
三角形的内角和
与三角形有关的角 三角形的外角和
内角与外角的关系
三角形
锐角三角形
斜三角形
按角分 钝角三角形
直角三角形
不等边三角形
按边分 底边和腰不相等的等腰三角形
等腰三角形
等边三角形
定义
多边形 多边形的内外角和
镶嵌
二、知识要点回顾
1、三角形的三边关系:
(1)、三角形两边之和大于第三边
(2)、三角形两边之差小于第三边
2、判断三条已知线段a、b、c能否组成三角形
当a最长,且有b+c﹥a时,就能构成三角形。
3、确定三角形第三边的取值范围
两边之差﹤第三边﹤两边之和
4、三角形的三条高线(或高线所在直线)交于一点
锐角三角形三条高交于三角形内部一点
直角三角形三条高线交于直角顶点
钝角三角形三条高线所在直线交于三角形外部一点
5、三角形的三条中线交于三角形内部一点,这点被称为重心
6、三角形的三条角平分线交于三角形内部一点,这点被称为内心
7、三角形的主要线段
(1)三角形的高线定义
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线
(2)三角形角平分线的定义
三角形一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
(3)连接三角形一个顶点与它对边中点的线段叫做三角形的中线
8、三角形木架的形状不会改变,而四边形木架的形状会改变。这就是说,三角形具有稳定性,而四边形没有稳定性
9、三角形内角和定理
三角形内角和等于180°
10、三角形外角和定理
三角形外角和等于360°
11、三角形的外角与内角的关系
三角形的一个外角等于与它不相邻的两个内角的和
三角形的一个外角大于与它不相邻的任何一个内角
12、n边形的内角和等于(n-2)×180°,多边形的外角和都等于360°
13、镶嵌
(1)、拼接在同一个点的各个角的和等于360°
(2)、任意三角形一定可以镶嵌
(3)、任意四边形一定可以镶嵌
(4)、正六边形可以镶嵌
注意:只用正五边形、正八边形一种图形不能镶嵌
第7章 三角形 练习课
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
练习目标:
通过练习,加强学生对已知知识的掌握和灵活运用。
练习过程:
一选择
1、三角形三个内角的度数分别是(x+y)°,(x-y)°,x°,且x﹥y﹥0,则该三角形有一个内角为( ) A 30° B 45° C 60° D 90°
2、把14cm长的细铁丝截成三段,围成不等边三角形,并且使三边长均为整数,那么( )
A 只有一种截法 B 只有两种截法 C 有三种截法 D 有四种截法
3、等腰三角形的腰长为a,底为x,则的取值范围是( )
A 0﹤x﹤2a B 0﹤x﹤a C 0﹤x﹤a/2 D 0﹤x≤2a
4、一个正多边形的每一个内角都是120°,这个多边形是( )
A 正四边形 B 正五边形 C 正六边形 D 正七边形
5、一个多边形木板,截去一个三角形后(截线不经过顶点),得到新多边形内角和为2160°,则原多边形的边数为( )A 13条 B 14条 C 15条 D 16条
6、下列说法中,错误的是( )
A 一个三角形中至少有一个角不大于60° B 有一个外角是锐角的三角形是钝角三角形C 三角形的外角中必有两个是钝角 D 锐角三角形中两锐角的和必小于60°
A
二填空
1、∠B=100°,∠A=∠C,则∠C= ;
2、2∠A=∠B+∠C,则∠A=
3、如右图, 是⊿ACD的外角
∠ADB﹦115°,∠CAD﹦80°,则∠C﹦
B D C
4、三角形的两边为7cm和5cm,则第三边x的取值范围是
5、直角三角形的两锐角相等,则每个锐角等于
6、在⊿ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大30°,则∠C的外角为 度,这个三角形是 三角形。
7、如下左图,AD是BC边上的高,BE是⊿ABD的角平分线,∠1=40°,∠2=30°,则∠C=
∠BED= A A
1 2
E
B C B C
D D
8、如上右图,已知:AD是△ABC的中线,△ABC的面积为50cm2,△ABD的面积是_______.
有一六边形,截去一三角形,内角会发生怎样的变化,请根据图示说明
9、如图所示,D是△ABC中BC边上一点,
试说明2AD<AB+BC+AC。
A
B C
D
10、已知两条线段的长分别是3cm和8cm,要想拼成一个三角形,且第三条线段a的长为奇数,问第三条线段应取多长?
11、如图所示,在⊿ABC中,DE∥BC,F是AB上一点,FE的延长线交BC的延长线于点G,试说明∠EGH和∠ADE的关系
A
F
D E
B
C G H
12、已知a、b、c为⊿ABC的三边长,且b、c满足(b-2)2+∣c-3∣=0,a为方程
∣x-3∣=2的解,求⊿ABC的周长,并判断⊿ABC的形状。
13、在⊿ABC中,∠ABC和∠ACB的角平分线相交于点O,试探索∠BOC与∠A的关系。
︶
︶
1
2
︶
︶
1
2
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第7章 三角形 ★ 7.1 与三角形有关的线段
—— 7.1.1 三角形的边(第1课时)
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
学习目标:
结合具体实例,在认识三角形概念及其基本要素的基础上,学会三角形的表示方法,掌握三角形三边之间的关系;通过观察、操作、交流和反思,获得必需的数学知识,发展空间概念,推理能力和有条理的表达能力。
学习重点:
三角形三边关系的探究与归纳
学习难点:
三角形三边关系的应用
学法指导:
在教师的指导下,学生自己探索和归纳学习知识,加深对所学内容的理解,进一步体会数学知识来源于实际生产和生活。
学习过程:
一、创设情景,新知导入:
三角形是常见的几何图形之一,从自然界景观到微型模型,从建筑物到艺术作品,在日常生活中到处都能找到三角形的影子,你能举出这样的一些实例吗?
二、探究学习
问题一:观察下图:
说说看,上面的三种图形是三角形吗?
如图1所示,如果它是三角形,你能用文字叙述出什么是三角形吗?
A
C b
B C
a
(图1)
从三角形的定义中,我们应注意的是:
①三角形是由三条线段组成的。②此三条线段不共线。③此三条线段首尾顺次连接。④三角形是一个平面图形
问题二:如图一,“三角形”可以用符号“ ”表示。记作“ ”,读作“三角形ABC”。
例:说出图2有多少个三角形?并用符号去表示它们。(请根据注意三角形的定义)
P
E
F G
H
Q (图2)
问题三:三角形的形状、大小和位置由它的三个顶点确定。三角形相邻两边的公共端点叫做三角形的顶点。如图1,“三角形ABC” 有 顶点,它们分别是顶点 ,顶点 ,顶点 。
问题四:组成三角形的三条线段叫做三角形的边。如图1,“三角形ABC”有 边,它们分别是线段 ,线段 ,线段 。有时候,三角形的三边我们也可以用a、b、c来表示。一般地,顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作C。
问题五:三角形相邻两边所组成的角叫做三角形的内角,简称三角形的角。如图1,“三角形ABC”有 内角,它们分别是 , , 。
综合练习:如图3
D
①图中有几个三角形,用符号表示这些三角形和各自的边
A
E
②以AB为边的三角形有哪些?
B C
(图3)
③以E为顶点的三角形有哪些? ④以∠D为角的三角形有哪些?
问题六:按照三角形内角的大小,我们可以将三角形分为锐角三角形,直角三角形,钝角三角形。如下图4是 ,如下图5是 ,如下图6是 。
A A A
C
B C B B C
图4 图5 图6
问题七:根据问题六,我们想一想,如果按照边的关系,我们可以将三角形分为 三角形, 三角形, 三角形。如下图7,下图8,下图9分别是什么三角形?
A A A
B C B C B C图7 图8 图9
(图7是 三角形) (图8是 三角形) (图9是 三角形)
在等腰三角形中,相等的两边叫做腰,另一边叫做底,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
等边三角形是特殊的等腰三角形,即底边和腰相等的等腰三角形。
★根据问题七,三角形按边相等关系分类如下:
不等边三角形
底边和腰不相等的等腰三角形
三角形 等腰三角形
等边三角形
问题八:任意画一个三角形,如图10,假设一只小虫从点B出发,沿三角形的边爬到点C,它有几条线路可以选择?各条线路的长一样吗?
A
B C
( 图10 )
对于任意一个△ABC,如果把其中任意两个顶点(例如B、C)看成定点,由“两点的所有连线
中,线段最短”,可以得到:
AB+AC﹥BC A
同样,若把顶点A、C看作定点,可以得到:
AB+BC﹥AC
若把顶点A、B看作定点,可以得到:
BC+AC﹥AB
一般地,我们有: B C
三角形两边之和大于第三边。
问题九:【动手操作】请同学们根据下图11,图12,图13,用直尺量出三个三角形的三边长度,并填入横线上。
A b a b a b
C c
C
(图11) (图12) (图13)
图11: 图12: 图13:
a= a= a=
b= b= b=
c= c= c=
★计算每个三角形的任意两边之差,并与第三边比较,你能得到什么结论
【自我学习】:请同学们看教材P64,看例题,看解题过程,有看不懂的地方向老师提出疑问。
三、盘点收获
本节课我们学习了三角形的概念及基本要素,重点研究了三角形的三边关系。
(1)从三角形三边关系中,我们可知三角形的三边相互制约——任意两边之和大于第三边,且任意两边之差小于第三边。
(2)判断a、b、c三条线段能否组成一个三角形,应注意: a+b>c,b+c>a,a+c>b。三个条件缺一不可。或者是:当a最长,且有b+c﹥a时,就能构成三角形。
四、达标检测
1、下列各组数字表示三条线段,其中可以组成三角形的是( )
A 12、4、6 B 3、4、5 C 4、15、6 D 2、5、7
2、三角形一边是5,一边是13,则第三边的取值范围是( )
A 5﹤x﹤13 B 8﹤x﹤18 C x﹥8 D x﹤18
3、⊿ABC的三边长分别为整数,周长为11,且有一边为4,则这个三角形可能有的最大边长是( )
A 5 B 5 C 6 D 7
4、各边长均为整数,且三边均不相等的三角形的周长小于13,这样的三角形有( )
A 1个 B 2个 C 3个 D 4个
5、三角形两边分别为4和5,第三边为其中一边的2倍,则第三边长为 。
6、三角形的一边是5,另一边是8,周长恰好是5或8的倍数,则第三边长为 。
7、三角形中有两边长为7和2,第三边为奇数,则三角形周长为 。
8、有长为12、7、5、4的四根木棒,用其中三根组成三角形可有几种方法?为什么?
9、如图所示,小光从家到学校有两条路,一条是BAC,一条是BDEC,请问二者中哪一条较近,为什么?
A
D E
B C
10在⊿ABC中,AB﹦AC,AC边上的中线BD把⊿ABC的周长分为12cm和15cm两部分,求三角形的各边长。
A
D
B C
11已知⊿ABC的周长为48,最大边与最小边之差为14,另一边与最小边的和为25,求⊿ABC各边的长。
12、如图所示
①图中共有多少个三角形?并把它们写出来。
A
②线段AE是哪些三角形的边?
③∠B是哪些三角形的角? B D E C
13、如图所示 C
①图中有多少个三角形,它们分别是哪些?
B
②⊿ADC的顶点分别是哪些?
F
∠C的对边有哪些?
A D E
5、教(学)后反思
第7章 三角形 ★ 7.1 与三角形有关的线段
—— 7.1.2 三角形的高、中线与角平分线(第2课时)
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
学习目标:
了解三角形的高、中线与角平分线,并能在具体的三角形中画出它们,通过观察、操作、想象、推理和交流的基础上,发展空间概念,推理能力和有条理的表达能力。
学习重点:
三角形的高、中线与角平分线的概念
学习难点:
准确画出三角形的高、中线与角平分线
学法指导:
在教师的指导下,学生自己探索和归纳学习知识,在动手操作中发现规律,掌握新知
学习过程:
一、创设情景,新知导入:
上一节课,我们认识了三角形及其基本要素:边、角、顶点,请同学们回忆一下,什么样的图形是三角形?三角形三条边之间有什么样的关系?
在前面,我们学习过“过一点画已知直线的垂线”,还能记得它的画法吗?在图一上操作一下 ,并与同桌交流一下自己的画法。 A
·
(图一)
B D C
(图二)
二、探究学习
问题一:从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形这边的高,简称三角形的高。如图二所示。线段AD是BC边上的高。
用同样的方法,你能画出锐角△ABC(图三)的另两条边上的高吗?
注意:标明垂直的记号( )和垂足的字母。 A
如果用折纸的办法能等到它们吗?和同桌进行交流。
观察你的做法,想想这三条高之间有怎样的位置关系?
将你的结果与同桌进行交流。
锐角三角形的三条高 。
再进一步想:锐角三角形的三条高是在三角形的 B C
内部还是在外部? D
锐角三角形的三条高都在 。 (图三)
★ 动手操作:画一个直角三角形。 A
画出直角三角形的三条高,观察它们有怎样的位置关系?
将你的结果与前后同桌进行交流。
直角三角形的三条高 。直角边AC边上的高 是,
直角边BC边上的高 是,斜边AB边上的高 是。 C B
★ 动手操作:画一个钝角三角形。
钝角三角形的三条高交于一点吗?它们所在的直线交于一点吗?将你的结果与同伴进行交流。
A
①钝角三角形的有 高,一条高在三角形的
(内部还是外部),另外的高在三角形的 (内部还是外部)。
②钝角三角形的高交于一点吗? B C
③钝角三角形三条高所在的直线交于一点吗?如果相交于一点,它们相交于钝角三角形的内部还是外部?
归纳:三角形三条高的特性。
锐角三角形 直角三角形 钝角三角形
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三条高所在的直线的交点的位置
问题二:在三角形中,连接一个顶点与它对边的中点的线段,叫做这个三角形的中线。
如图四: A
在图四中,D是BC的中点,线段AD是△ABC的中线。
由定义可知:如果线段AD是△ABC的中线,那么有:
BD=DC=1/2BC
在一个三角形中,有几条中线呢?它们的位置关系又如何呢?请同学们画一画,议一议。(分别画锐角三角形,钝角三角形,直角三角形)
B D C
A (图四) A A
B C B C B C
(锐角三角形) (钝角三角形) (直角三角形)
通过以上作图,我们知道,一个三角形的中线共有 条,它们存在于三角形的 ,并且三角形的三条中线 于一点。我们把这一点叫做重心。
如果通过折纸的方法,能得到它们吗?你是怎么做的,和同伴进行交流。
问题三:在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线。
如图五: A
在图五中,如果AD是∠BAC的角平分线,那么有:
∠BAD=∠DAC=1/2∠BAC
在一个三角形中,有几个角平分线呢?它们的位置关系又如何呢?请同学们画一画,议一议。(分别画锐角三角形,钝角三角形,直角三角形)
B D C
A (图五) A A
(钝角三角形) (直角三角形)
(锐角三角形)
B C B C B C
通过以上作图,我们知道:一个三角形一共有 条角平分线,都在三角形的 ,它们 于一点。我们把这点叫做三角形的内心。
如果通过折纸的方法,能得到它们吗?你是怎么做的,和同伴进行交流。
观察下图,三角形的角平分线与角的平分线有什么区别? A
A
D
B D C B C
结论是: 。
三、盘点收获
本节课,我们主要探究了三角形的高、中线和角平分线。
三角形的高不一定都在三角形的内部:锐角三角形的三条高都在三角形的内部;直角三角形中,有两条高恰好是它的两条直角边;钝角三角形中,两锐角所对边上的高都在三角形的外部。三角形的三条高所在的直线相交于一点。三角形的高是线段。
三角形的中线、角平分线也都是线段;三角形的三条中线、三条角平分线都相交于一点,都在三角形的内部;这一点我们分别称之为重心和内心。
三角形的角平分线与角的平分线既有联系,也有区别,前者是线段,后者是射线。
四、达标检测
1、如图,有一块三角形的土地,需要把其分成4等份给四户农民耕种,只准分成三角形,你有多少种分法?(画出分解图形)
2、如图所示,⊿ABC中,∠BAC是钝角,完成下列作图。 A
①∠BAC的平分线AD
②AC边上的中线BE
B C
③AC边上的高BF
3、如图,若AB⊥CD,垂足是D,则CD是哪些三角形的高?若E是边BC的中点,则AE是哪个三角形的中线?
A
D
B E C
4、若有一条公共边的两个三角形称为一对“共边三角形”,则如图(1)所示中以BC为公共边的“共边三角形”有( ) A 2对 B 3对 C 4对 D 6对
A D
A Ⅱ
E
D Ⅰ O Ⅳ
Ⅲ
B C B C
图(1) 图(2)
5、如图(2)所示,有一个四边形牧场,被对角线分割成4个牧场,若草场中可放4只羊,草场中可放6只羊,草场中可放8只羊,则草场中可放( )
A 10只羊 B 11只羊 C 12只羊 D 13只羊
6、如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是( )
A 锐角三角形 B 钝角三角形 C 直角三角形 D 不能确定
7、关于三角形的三条中线,下列说法中正确的是( )
A 必在三角形的内部 B 必在三角形的外部
C 必和三角形的一条边重合 D 以上皆有可能
8、如下图所示,已知⊿ABC,过点A画一条平分三角形面积的直线。
A
A
D
B C B E C
9、如图所示,D、E分别为⊿ABC的边AC、BC的中点,则下列说法中,不正确的是( )
A DE是⊿BDC的中线 B BD是⊿ABC的中线 C AD﹦DC,BE﹦EC D ∠C的对边是DE
10、在图(3)中,互不重叠的三角形共有4个,在图(4)中,互不重叠的三角形共有7个,在图(5)中,互不重叠的三角形共有10个,……则在第 n个图形中,互不重叠的三角形共有多少个?(用含n的式子表示)
图(3) 图(4) 图(5)
11、如图所示,在⊿ABC中,DE∥BC,EF∥AB,BE平分∠DBF交DF于点O,则EO是否是∠DEF的角平分线?请说明理由。
A
D E
O
B F C
5、教(后)学反思
第7章 三角形 ★ 7.1 与三角形有关的线段
—— 7.1.3 三角形的稳定性(第3课时)
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
学习目标:
通过观察和实际操作得到三角形具有稳定性,四边形没有稳定性的结论;以及三角形稳定性和四边形没有稳定性在生产和生活中的应用
学习重点:
了解三角形稳定性在生产、生活中的实际应用
学习难点:
准确使用三角形稳定性于生活之中
学法指导:
观察、操作、探究、交流
学习过程:
一、创设情景,新知导入:
盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做?
你的理由是:
二、探究学习
问题一:如图一:将三根木条用钉子钉成
一个三角形木架,然后扭动它,它的形状会改
变吗?
(图一)
问题二:如图二,将四根木条用钉子钉成
一个四边形木架,然后扭动它,它的形状会改
变吗?
(图二)
问题三:在四边形木架上再钉一根木条,将
它的一对顶点连接起来,然后扭动它,这时木架
的形状还会改变吗?为什么?
(图三)
通过我们的实际操作,我们发现,三角形木架的形状 (如图一),而四边形的形状 (如图二)。
说明:三角形是具有 的图形,而四边形没有 。
通过图三发现,斜钉一根木条的四边形木架的形状 。这是因为斜钉一根木条后,四边形变成了两个 ,由于三角形具有 ,窗框在未安装好之前也不会变形。
问题四:三角形的稳定性在生活中有广泛的应用,如下图,除外。你能举出相应的例子吗
(屋顶钢架)
问题五:四边形的不稳定性也有广泛的应用,如下图所示,除外,你还能举出其他的实例吗?
三、盘点收获
我们通过操作,了解了三角形具有稳定性,四边形不具有稳定性的特点,也就是说,一个三角形的三条边固定了,三角形的形状和大小就完全确定了。所有的多边形中,只有三角形具有稳定性。
四、达标检测
1下列图形中不具有稳定性的是( )
2撑上支撑后的自行车能稳稳地停在地上,是因为自行车的两个轮胎与地面以及支撑形成了一个三角形,三角形具有( )。
5、教(学)后反思
第7章 三角形 ★ 7.2 与三角形有关的角
—— 7.2.1 三角形的内角(第1课时)
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
学习目标:
1、经历实验活动的过程,得出三角形的内角和定理,能用平行线的性质推出这一定理
2、能应用三角形内角和定理解决一些简单的实际问题
学习重点:
三角形内角和定理
学习难点:
三角形内角和定理的推理过程
课前准备:
每个学生准备好两个由硬纸片剪出的三角形
学法指导:
在教师的指导下,学生自己探索和归纳学习知识,加深对所学内容的理解。
学习过程:
一、创设情景,新知导入:
在前面我们学习了与三角形有关的线段,请同学们回忆一下所学内容,回答如下问题:
①什么是三角形与三角形的表示方法 A
②三角形的主要线段
③三角形三边的关系 B C
二、探究学习
问题一:【动手操作】请同学们任意画一个三角形,并用量角器测量一下,每个内角的度数是多少?三角形三个内角的度数和又是多少?同伴之间交流。
通过我们的操作,我们可以得出结论:
三角形三个内角的和等于 。
问题二:在实际生活中,由于形状不同的三角形有无数个,我们不可能用度量的方法一一验证所有三角形。那么我们该如何求证上面结论的正确性呢?
下面请同学们拿出我们事先准备好的两个硬纸片三角形,并在硬纸片三角形上标出三个内角的编码,按下面图1、图2、图3方式拼合在一起,能得到什么?在这个操作过程中,你能发现证明的思路吗?
(图1) (图2)
想一想,如果我们不用剪,拼办法,可不可以用推理论证的方法来说明上面结论的正确性呢?
★ 操作应用:
已知:△ABC (图4) A
求证:∠A+∠B+∠C=180° E
方法一:
证明:在△ABC的外部以CA为边作
∠ACE=∠A。延长BC至D
∵ ∠ACE=∠A
∴ CE∥BA(内错角相等,两直线平行) B D
∴ ∠DCA=∠B( ) C
∵ ∠BCA+∠ACE+∠ECD=180°(平角定义) (图4)
∴ ∠BCA+∠A+∠B=180°(等量代换)
方法二:(图4)
证明:延长BC至D,过点C作CE∥BA
则∠A=∠ACE( )
∠B=∠ECD ( )
∵ ∠BCA+∠ACE+∠ECD=180°(平角定义
∴ ∠BCA+∠A+∠B=180°(等量代换) A
方法三:(图5) E F
证明:过点A作EF∥BC
则 ∠EAB=∠B ( )
∠FAC=∠C ( )
∵ ∠EAB+∠BAC+∠CAF=180°(平角定义)
∴ ∠B+∠BAC+∠C=180°(等量代换) B C
(图5)
通过以上推导过程,可以看出,证明是由题设(已知)出发,经过一步步的推理,最后推出结论(求证)正确的过程。
★ 例题探讨:
C岛在A岛的北偏东方向,B岛在A岛的北偏东方向,C岛在B岛的北偏西方向,从C岛看A、B两岛的视角是多少度?
分析:A、B、C三岛的连线构成△ABC,所求的∠ACB是△ABC的一个内角。如果能求出∠CAB、∠ABC,就能求出∠ACB。
解:∠CAB=∠BAD-∠CAD=80°-50°=30°
由AD∥BE,可得:
∠BAD+∠ABE=180°( )
所以:
∠ABE=180°-∠BAD=180°-80°=100°
∠ABC=∠ABE-∠EBC=100°-40°=60°
在△ABC中,
∠ACB=180°-∠ABC-∠CAB=180°-60°-30° =90°
答:从C岛看A、B两岛的视角是90°
三、盘点收获
知识要点 总结 注意问题 解题方法总结
三角形内角和定理 三角形的三个内角的和等于180° 此定理应用的前提条件是在同一个三角形中。 (1)已知两角或两角的和,求另一个角,利用三角形内角和定理。
四、达标检测
1、一个三角形最多有 个直角,最多有 个钝角。
2、若一个三角形的三个内角之比为2:3;4,则这三个内角的度数分别是 , , 。
3、在△ABC中,若∠A+∠B=2∠C,则∠C= °。
α
4、如图:∠α= 。 48°
32° 44°
5、在△ABC中,∠A=∠B+∠C,则△ABC是 三角形。
6、在△ABC中,∠C=2(∠A+∠B),则∠C= 。
7、一个三角形的三个内角的度数比是2:3:7,这个三角形是( )
A 直角三角形 B 等腰三角形 C 锐角三角形 D 钝角三角形
8、如图(1)所示,若∠1﹥∠2,则∠1、∠2、∠3用“﹤”连结,正确的是( )
A ∠3﹤∠2﹤∠1 B ∠2﹤∠1﹤∠3 C ∠2﹤∠3﹤∠1 D 以上都不对
A
A D
1
O
2 3
B E
C B C
图(1) 图(2) A
9、如图(2),所示,∠A﹢∠B﹢∠C﹢∠D﹢∠E﹦
1
10、如图(3)所示,∠1、∠2、∠3、∠4满足的关系式是( )
A ∠1﹢∠2﹦∠3﹢∠4 B ∠1﹢∠2﹦∠4-∠3 C
C ∠1﹢∠4﹦∠2﹢∠3 D ∠1﹢∠4﹦∠2-∠3
A E
2
O 4 3 B
图(3)
E
B 2 1 C
图(4)
D
11、 如图(4)所示,下列说法中错误的是( )
A ∠2﹦∠A﹢∠B﹢∠D B ∠1﹦∠2-∠D C ∠2﹦∠A﹢∠D D ∠2﹥∠1﹥∠A
12、如图(5)所示,∠A﹦∠C,CD⊥AB于D,交AE于F,试判定⊿AEB的形状,并说明你的理由。 A
D
F
B C
E
13、如下图(1)所示,在⊿ABC中,AE平分∠BAC(∠C﹥∠B),F为AE上一点,且FD⊥BC于点D。 (1)试推导∠EFD与∠B、∠C之间的大小关系。
(2)如图(2),当点F在AE的延长线上时,其余条件都不变,判断你在(1)中推导的结论是否还成立? A A
F
D
B C B E C
E D
F
五、教(学)后反思
第7章 三角形 ★ 7.2 与三角形有关的角
—— 7.2.2 三角形的外角(第2课时)
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
学习目标:
1、使学生在操作活动中,探索并了解三角形的外角的两条性质
2、利用学过的定理论证这些性质
3、能利用三角形的外角性质解决实际问题
学习重点:
三角形的外角性质;三角形的外角和定理
学习难点:
三角形外角的定义及定理的论证过程
学法指导:
学练结合
学习过程:
一、创设情景,新知导入:
上节课,我们学习了三角形内角和定理,其定理内容是什么?
如下图把的一边BC延长到D,得,它不是三角形的内角,那它是三角形的什么角?
什么是三角形的外角?
二、探究学习
问题一:观察图1,思考: A
①一个三角形有多少个外角? 不相邻
内角 相邻内角
②请根据图1完成下面填空
∠A+∠B+∠1= ( ) 外角
1
∠ACD+∠1= ( )
B C D
③根据上面的填空,我们得出下列关系: (图1)
∠ACD=∠A+∠B 其理由是 。
一般地,有下面的结论:
三角形的一个外角等于与它不相邻的两个内角的和。
由上面的结论,可以得到:
三角形的一个外角大于与它不相邻的任何一个内角。
根据图1,完成选择( ﹥ ﹤ ):①∠ACD ∠A ②∠ACD ∠B
问题2:观察图2给予的提示,求证:∠1+∠2+∠3=360°1 A
已知:
求证:∠1+∠2+∠3=360°
证明:
2
B
3 (图2) C
经过刚才我们的证明,可以得到:三角形的外角和等于 。
除了刚才的证明方法外,我们也可以用下面的方法去证明。根据下图3的提示,想一想,该怎样证明∠1+∠2+∠3=360°,写出你的证明过程。 4
1 D
A
2
B
3 (图3) C
三、盘点收获
知识要点 总结 注意问题 解题方法总结
三角形外角的概念及性质 三角形的一边与另一边的延长线组成的角,叫做三角形的外角。性质1三角形的一个外角等于与它不相邻的两个内角的和。性质2三角形的一个外角大于与它不相邻的任何一个内角。 添加辅助线把问题转化为三角形问题,实现条件的转化。 (2涉及角的不等关系,利用“三角形的一个外角大于与它不相邻的任何一个内角”来解题。
四、达标检测
1、三角形的外角和是指三角形所有外角的和。( )
2、三角形的外角和等于它内角和的2倍。( )
3、三角形的一个外角等于两个内角的和。( )
4、三角形的一个外角等于与它不相邻的两个内角的和。( )
5、三角形的一个外角大于任何一个内角。( )
6、三角形的一个内角小于任何一个与它不相邻的外角。( )
7、三角形的三个外角中最多有 锐角,最多有 个钝角,最多有 个直角。
8、如图4,X=
9、如图5,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连EF, 则∠1,∠2,∠3的大小关系是_________
(图4) (图5)
10、如下图(1),求出∠A+∠B+∠C+∠D+∠E+∠F的度数
11、如上图(2),求出∠A+∠B+∠C+∠D+∠E+∠F的度数
5、教(学)后反思
第7章 三角形 ★ 7.3 多边形及其内角和
—— 7.3.1 多边形(第1课时)
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
学习目标:
了解多边形及有关概念,理解正多边形及其有关概念
学习重点:
了解多边形及其有关概念,理解正多边形及其有关概念
学习难点:
多边形定义的准确理解
学法指导:
自学为主,教师指导
学习过程:
一、创设情景,新知导入:
前面我们学习了三角形,你能说说学习了哪些有关三角形的知识?
①观察图1,你能说出三角形的定义吗?
(图1) (图2)
②观察图2,既然我们已经知道什么叫三角形,
你能根据三角形的定义,说出什么叫四边形吗?
③观察图3,什么叫五边形呢? (图3) (图4)
二、探究学习
问题一:通过上面三角形,四边形,五边形的定义,我们知道了什么是三角形,四边形,五边形。那么多边形的定义又是什么?(图5)
问题二:通过对图1—图4的观察,我们知道:多边形是按组成它的线段的条数而进行分类的,三角形是最基本的多边形。那么什么是多边形的内角?多边形的外角?
对于图2来说,它的内角分别是: 、 、 、 。
对于图3来说,它的内角分别是: 、 、 、 、 。
对于图4来说,它的内角分别是: 、 、 、 、 、 。
因此我们说:多边形相邻两边组成的角叫做它的 。
观察图5,∠1是多边形ABCDE的一个 。
对于图2来说,它的外角有 个,对于图3来说,它的
外角有 个,对于图4来说,它的外角有 个,那么n边形
有 个外角。
(图5)
问题三:根据前面的学习内容,我们说,多边形的内角,边,外角有着一定的关系,请你填写下表,能发现它们之间的规律吗?
多边形的边数 3 4 5 6 7 … n
多边形内角的个数
多边形边的个数
多边形外角的个数
规律是:
问题四:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线。请将下列图形根据多边形对角线的定义,试着连接,从中寻找规律,完成表格的填写。
多边形的边数 3 4 5 6 7 n
从一个顶点引对角线的条数
分成的三角形的个数
规律是:从n边形的一个顶点可以引 条对角线,把多边形分成 个三角形。
问题五:观察图6,画出四边形ABCD的任何一条边,(如AB)所在的直线,整个四边形都在这条直线的同一侧,这样的四边形叫做凸四边形。而图7中的四边形ABCD就不是凸四边形,因为画CD(或BC)所在的直线,整个四边形不都在这条直线的同一侧。
A
D
B
(图6)
C
(图7)
类似地,画多边形的任何一条边所在的直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形。这是我们本节课讨论的内容。
问题六:三角形如果三条边都想的,三个角也都相等,那么这样的三角形就叫做正三角形。如果多边形各条边都相等,各个角也都相等,那么这样的多边形就叫做正多边形。(如下图所示)
(正三角形) (正四边形) (正五边形) (正六边形) (正八边形)
三、盘点收获
在一个平面内,由一些线段首尾顺次连结组成的图形叫做多边形。
各个角都相等,各条边都相等的多边形叫做正多边形。
n边形的对角线等于[n×(n-3)]÷2.
四、达标检测
(一)、判断题.
1.由四条线段首尾顺次相接组成的图形叫四边形.( )
2.由不在一直线上四条线段首尾次顺次相接组成的图形叫四边形.( )
3.由不在一直线上四条线段首尾顺次接组成的图形,且其中任何一条线段所在的直线、使整个图形都在这直线的同一侧,叫做四边形.( )
4.在同一平面内,四条线段首尾顺次连接组成的图形叫四边形.( )
(二)、填空题.
1.连接多边形 的线段,叫做多边形的对角线.
2.多边形的任何 所在的直线,整个多边形都在这条直线的 ,这样的多边形叫凸多边形.
3.各个角 ,各条边 的多边形,叫正多边形.
(三)、解答题.
1.在正四边形ABCD中,你能用四中不同的方法把正四边形的面积四等分吗?
2.如上图(2),O为四边形ABCD内一点,连接OA、OB、OC、OD可以得几个三角形?它与边数有何关系?
3.如上图(3),O在五边形ABCDE的AB上,连接OC、OD、OE,可以得到几个三角形?它与边数有何关系?
4.如上图(4),过A作六边形ABCDEF的对角线,可以得到几个三角形?它与边数有何关系?
五、教(学)后反思
第7章 三角形 ★ 7.3 多边形及其内角和
—— 7.3.2 多边形的内角和(第2课时)
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
学习目标:
1、使学生了解多边形的内角、外角等概念
2、能通过不同方法探索多边形的内角和与外角和公式,并会应用它们进行有关计算
学习重点:
1、多边形的内角和公式
2、多边形的外角和公式
学习难点:
多边形的内角和定理的推导
学法指导:
探究学习
学习过程:
一、创设情景,新知导入:
1我们知道三角形的内角和为180°。
2我们还知道,正方形(正四边形)四个角都等于90°,那么它的内角和为360°,同样,长方形的内角和也是360°。
3正方形和长方形都是特殊的四边形,其内角和为360°。那么,任意一个四边形的内角和是否也是360°呢?
二、探究学习
问题一:请同学们画一个任意四边形,用量角器量出它的四个内角度数,计算它们的和,与同桌进行交流结果。
结论:任意一个四边形的内角和等于 。
我们能利用三角形内角和定理去证明我们得出的这个结论吗?
问题二:根据下面提供的图形和文字,做一做,填一填,找出规律。
A F
D A A
A
D E
B B B B D
C C C C
(图1) (图2) (图3) (图4)
①如图1,三角形ABC的内角和是多少度?( )
②如图2,图中有几个三角形?( )四边形的内角和是多少度?( )
③如图3,图中有几个三角形?( )五边形的内角和是多少度?( )
④如图4,图中有几个三角形?( )六边形的内角和是多少度?( )
多边形的边数 3 4 5 6 7 … n
分成三角形的个数
多边形的内角和
由此,我们得出:n边形的内角和= 。
问题三:要得到多边形的内角和必需通过“三角形内角和定理”来完成,就是把一个多边形分成几个三角形。除利用对角线把多边形分成几个三角形外,还有其他的分法。(以五边形为例)
分法一:观察图5,在五边形ABCDE内取一点O,连接OA、OB、OC、OD、OE,则得五个三角形。其五个三角形的内角和为5×180°,而∠1、∠2、∠3、∠4、∠5(这五个角合在一起变成周角)不是五边形的内角,应减去,所以:五边形的内角和为5×180°-2×180°=(5-2)×180°=540°
(图5)
如果五边形变成n边形,用同样的方法也可以得到n个三角形的内角和减去一个周角,即可得:n边形内角和=n×180°-2×180°=(n-2)×180°。
分法二:观察图6,在五边形的边AB上取一点O,连接OE、OD、OC,则可以得到(5-1)个三角形,而∠1、∠2、∠3、∠4不是五边形的内角,应舍去。
所以:五边形的内角和为(5-1)×180°-180°=(5-2)×180°
用同样的方法,也可以把n边形分成(n-1)个三角形,把不是n边形内角的∠AOB舍去,即可得n边形的内角和为(n-2)×180°
(图6)
问题三:图图7,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和。六边形的外角和等于多少?
(1)任何一个外角同与它相邻的内角有什么关系?
(2)六边形的6个外角加上与它们相邻的内角,所得的总和是多少?
(3)上述总和与六边形的内角和,外角和有什么关系?
(图7)
如果将图7中的六边形换成n边形(n的值是不小于3的任意整数)也可以得到同样的结果吗?
由问题三的探究,我们可以得到:多边形的外角和等于 。
所以我们说,多边形的外角和与它的边数无关。
对此,我们也可以像以下这样理解,为什么多边形的外角和等于360°
如右图,从多边形的一个顶点A出发,沿多边形各边走过
各顶点,再回到A点,然后转向出发时的方向,在行程中所转
的各个角的和就是多边形的外角和,由于走了一周,所得的各
个角的和等于一个周角,所以多边形的外角和等于360
三、盘点收获
知识要点 总结 注意问题 解题方法总结
多边形内角和定理 n边形内角和等于(n-2)×180° 内角和随多边形边数的改变而改变。 (1)常利用对角线将多边形问题转化为三角形问题解决。(2)定值问题长从多边形外角和的方向来考虑。
多边形外角和定理 多边形的内角和等于360° 多边形的外角和是定值。
四、达标检测
(一)、判断题.
1.当多边形边数增加时,它的内角和也随着增加.( )
2.当多边形边数增加时.它的外角和也随着增加.( )
3.三角形的外角和与一多边形的外角和相等.( )
4.从n边形一个顶点出发,可以引出(n一2)条对角线,得到(n一2)个三角形.( )
5.四边形的四个内角至少有一个角不小于直角.( )
(二)、填空题.
1.一个多边形的每一个外角都等于30°,则这个多边形为 边形.
2.一个多边形的每个内角都等于135°,则这个多边形为 边形.
3.内角和等于外角和的多边形是 边形.
4.内角和为1440°的多边形是 .
5.一个多边形的内角的度数从小到大排列时,恰好依次增加相同的度数,其中最小角为100°,最大的是140°,那么这个多边形是 边形.
6.若多边形内角和等于外角和的3倍,则这个多边形是 边形.
7.五边形的对角线有 条,它们内角和为 .
8.一个多边形的内角和为4320°,则它的边数为 .
9.多边形每个内角都相等,内角和为720°,则它的每一个外角为 .
10.四边形的∠A、∠B、∠C、∠D的外角之比为1:2:3:4,那么∠A:∠B:∠C:∠D= .
11.四边形的四个内角中,直角最多有 个,钝角最多有 个, 锐角最多有 个.
12.如果一个多边形的边数增加一条,那么这个多边形的内角和增加 ,外角和增加 .
(三)、选择题.
1.多边形的每个外角与它相邻内角的关系是( )
A.互为余角 B.互为邻补角 C.两个角相等 D.外角大于内角
2.若n边形每个内角都等于150°,那么这个n边形是( )
A.九边形 B.十边形 C.十一边形 D.十二边形
3.一个多边形的内角和为720°,那么这个多边形的对角线条数为( )
A.6条 B.7条 C.8条 D.9条
4.随着多边形的边数n的增加,它的外角和( )
A.增加 B.减小 C.不变 D.不定
5.若多边形的外角和等于内角和的和,它的边数是( )
A.3 B.4 C.5 D.7
6.一个多边形的内角和是1800°,那么这个多边形是( )
A.五边形 B.八边形 C.十边形 D.十二边形
7.一个多边形每个内角为108°,则这个多边形( )
A.四边形 B,五边形 C.六边形 D.七边形
8,一个多边形每个外角都是60°,这个多边形的外角和为( )
A.180° B.360° C.720° D.1080°
9.n边形的n个内角中锐角最多有( )个.
A.1个 B.2个 C.3个 D.4个
10.多边形的内角和为它的外角和的4倍,这个多边形是( )
A.八边形 B.九边形 C.十边形 D,十一边形
11.过多边形的一个顶点可以引9条对角线,那么这个多边形的内角和是( )
A 1620° B 1800° C 1980° D 2160°
12.八边形的对角线的条数是( )
A 9条 B 14条 C 20条 D 24条
13.如果把一个多边形的边数增加1倍,它的内角和是2160°,那么原来多边形的边数是( )
A 5条 B 6条 C 7条 D 8条
14.下面几个结论:①三角形的外角中最多只有一个锐角;②正n边形的内角度数等于180°-360°/n;③多边形的内角和不一定大于多边形的外角和;④n边形的边数每增加1条,对角线就增加 n条;⑤任何一个多边形中,锐角不超过3个。其中正确的有( 0
A 2个 B 3个 C 4个 D 5个
15.如图(1)所示,试求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
D
A G
E F
B C
图(1)
16.★探究题★ 过m边形的一个顶点有7条对角线,n边形没有对角线,k边形共有k条对角线,则(m-K)n为多少?
17.★开放题★ 如图,把正方形截下一个角后,得到的图形的内角和为多少
5、教(学)后反思
第7章 三角形 ★ 7.4 课题学习 镶嵌
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
学习目标:
1、会用正多边形无缝隙、不重叠第覆盖平面
2、让学生应用已有的数学知识和能力,探索和解决镶嵌问题的过程中,感受数学知识的价值,增强应用意识,获得各种体验
学习重点:
会用正多边形无缝隙、不重叠第覆盖平面
学习难点:
哪些多边形形状可以镶嵌平面图形
学法指导:
实际操作,感受体验带来的快乐
学习过程:
一、创设情景,新知导入:
观察提供的图片:
我们经常能看到各种建筑物的地板,观察地板,就能发现地板常用各种正多边形地砖砌成美丽的图案。
二、探究学习
问题一:镶嵌定义。
用一些形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙,不重叠的把平面的一部分完全覆盖,这就是平面图形的镶嵌。
注意:各种图形拼接后既要无缝隙,又不重叠。
利用镶嵌我们可以得到一些绚丽多
彩的图案。
问题二:【动手操作】 请同学们将准备好的图形,如边长相同的正三角形,正方形,正五边形,正六边形等拿出来,按提示要去操作。
(1)用边长相同的正三角形能否镶嵌?结论是:用边长相同的正三角形 镶嵌。
(2)用边长相同的正方形能否镶嵌?结论是:用边长相同的正方形 镶嵌。
(3)用边长相同的正五边形能否镶嵌?结论是:用边长相同的正五边形 镶嵌。
(4)用边长相同的正六边形能否镶嵌?结论是:用边长相同的正六边形 镶嵌。
根据我们刚才的实际操作拼接,想一想,镶嵌平面图案需要什么条件?
条件是:拼接在同一个点的各个角的和恰好等于 。
三、盘点收获
本节我们学习了在平面内如何镶嵌的知识。
知识要点 总结 注意问题 解题方法总结
平面镶嵌的定义 用一些不重叠摆放的多边形把平面的一部分完全覆盖,在几何里叫做平面镶嵌。 平面镶嵌既不能重叠也不能有空隙。 在进行平面镶嵌的图案设计问题中,要使拼接在同一个顶点的各个多边形的内角和等于360°。
平面镶嵌的条件 (1)拼接在同一点的各个角的和恰好等于360°(2)相邻的多边形有公共边,当所用的多边形为正多边形时,它们的边长应相等。 两个条件必须同时满足,缺一不可。
四、达标检测
1、在一个顶点处,若n边形的几个内角的和为 ,则此正n边形可铺满地面,没有空隙。
2、能用一种正多边形进行平面镶嵌的有 、 、
3、能用一种任意多边形进行平面镶嵌的有
4、如果只用圆、正五边形、矩形中的一种图形镶嵌整个平面,那么这个图形只能是
5、只用正三角形和正六边形地板铺地面,你有几种方案?
6、在一间长6m,宽3.5m的客厅地面上,要铺同种规格的正方形地砖,现在有““40cm×40cm”,“30cm×30cm”,“50cm×50cm”,“60cm×60cm”的地砖,请你设计一下,需要全部铺满,不能破地砖,不留一点空隙,也不多余,选哪一种规格,为什么?
7、如图所示,你能将一个正三角形分成8个大小、形状意义的直角三角形吗?若能,请你画出图形。
8、用m个正三角形和n个正六边形铺满地面,先求出m、n的值,再各自设计一种铺法,并作出设计的图形。
5、教(学)后反思
第7章 三角形 复习课
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
复习目标:
通过对本章知识结构图,加深本章知识的理解;
对知识点的归纳,是为了更好地的在解决本章知识的时候,能灵活运用。
复习过程:
一、三角形知识结构图:
三角形的边
与三角形 高线
有关的线段 中线
角平分线
三角形的内角和
与三角形有关的角 三角形的外角和
内角与外角的关系
三角形
锐角三角形
斜三角形
按角分 钝角三角形
直角三角形
不等边三角形
按边分 底边和腰不相等的等腰三角形
等腰三角形
等边三角形
定义
多边形 多边形的内外角和
镶嵌
二、知识要点回顾
1、三角形的三边关系:
(1)、三角形两边之和大于第三边
(2)、三角形两边之差小于第三边
2、判断三条已知线段a、b、c能否组成三角形
当a最长,且有b+c﹥a时,就能构成三角形。
3、确定三角形第三边的取值范围
两边之差﹤第三边﹤两边之和
4、三角形的三条高线(或高线所在直线)交于一点
锐角三角形三条高交于三角形内部一点
直角三角形三条高线交于直角顶点
钝角三角形三条高线所在直线交于三角形外部一点
5、三角形的三条中线交于三角形内部一点,这点被称为重心
6、三角形的三条角平分线交于三角形内部一点,这点被称为内心
7、三角形的主要线段
(1)三角形的高线定义
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线
(2)三角形角平分线的定义
三角形一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
(3)连接三角形一个顶点与它对边中点的线段叫做三角形的中线
8、三角形木架的形状不会改变,而四边形木架的形状会改变。这就是说,三角形具有稳定性,而四边形没有稳定性
9、三角形内角和定理
三角形内角和等于180°
10、三角形外角和定理
三角形外角和等于360°
11、三角形的外角与内角的关系
三角形的一个外角等于与它不相邻的两个内角的和
三角形的一个外角大于与它不相邻的任何一个内角
12、n边形的内角和等于(n-2)×180°,多边形的外角和都等于360°
13、镶嵌
(1)、拼接在同一个点的各个角的和等于360°
(2)、任意三角形一定可以镶嵌
(3)、任意四边形一定可以镶嵌
(4)、正六边形可以镶嵌
注意:只用正五边形、正八边形一种图形不能镶嵌
第7章 三角形 练习课
年级:七年级 科目:数学 执笔人: 审核:【 】
课型:新授课 授课班级:七年级【 】班 学生姓名:【 】
练习目标:
通过练习,加强学生对已知知识的掌握和灵活运用。
练习过程:
一选择
1、三角形三个内角的度数分别是(x+y)°,(x-y)°,x°,且x﹥y﹥0,则该三角形有一个内角为( ) A 30° B 45° C 60° D 90°
2、把14cm长的细铁丝截成三段,围成不等边三角形,并且使三边长均为整数,那么( )
A 只有一种截法 B 只有两种截法 C 有三种截法 D 有四种截法
3、等腰三角形的腰长为a,底为x,则的取值范围是( )
A 0﹤x﹤2a B 0﹤x﹤a C 0﹤x﹤a/2 D 0﹤x≤2a
4、一个正多边形的每一个内角都是120°,这个多边形是( )
A 正四边形 B 正五边形 C 正六边形 D 正七边形
5、一个多边形木板,截去一个三角形后(截线不经过顶点),得到新多边形内角和为2160°,则原多边形的边数为( )A 13条 B 14条 C 15条 D 16条
6、下列说法中,错误的是( )
A 一个三角形中至少有一个角不大于60° B 有一个外角是锐角的三角形是钝角三角形C 三角形的外角中必有两个是钝角 D 锐角三角形中两锐角的和必小于60°
A
二填空
1、∠B=100°,∠A=∠C,则∠C= ;
2、2∠A=∠B+∠C,则∠A=
3、如右图, 是⊿ACD的外角
∠ADB﹦115°,∠CAD﹦80°,则∠C﹦
B D C
4、三角形的两边为7cm和5cm,则第三边x的取值范围是
5、直角三角形的两锐角相等,则每个锐角等于
6、在⊿ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大30°,则∠C的外角为 度,这个三角形是 三角形。
7、如下左图,AD是BC边上的高,BE是⊿ABD的角平分线,∠1=40°,∠2=30°,则∠C=
∠BED= A A
1 2
E
B C B C
D D
8、如上右图,已知:AD是△ABC的中线,△ABC的面积为50cm2,△ABD的面积是_______.
有一六边形,截去一三角形,内角会发生怎样的变化,请根据图示说明
9、如图所示,D是△ABC中BC边上一点,
试说明2AD<AB+BC+AC。
A
B C
D
10、已知两条线段的长分别是3cm和8cm,要想拼成一个三角形,且第三条线段a的长为奇数,问第三条线段应取多长?
11、如图所示,在⊿ABC中,DE∥BC,F是AB上一点,FE的延长线交BC的延长线于点G,试说明∠EGH和∠ADE的关系
A
F
D E
B
C G H
12、已知a、b、c为⊿ABC的三边长,且b、c满足(b-2)2+∣c-3∣=0,a为方程
∣x-3∣=2的解,求⊿ABC的周长,并判断⊿ABC的形状。
13、在⊿ABC中,∠ABC和∠ACB的角平分线相交于点O,试探索∠BOC与∠A的关系。
︶
︶
1
2
︶
︶
1
2
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
