正比例函数
图片预览





文档简介
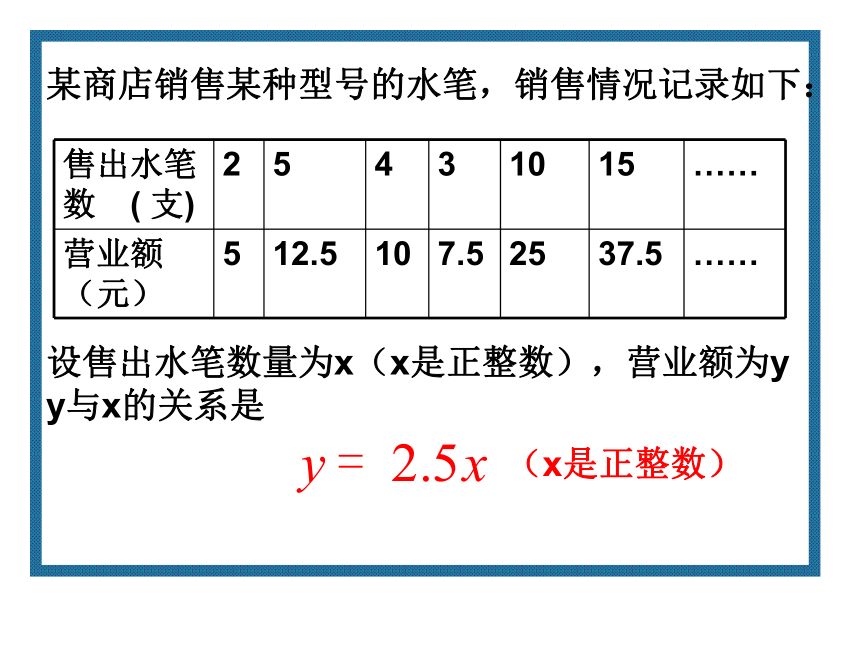
课件15张PPT。正比例函数某商店销售某种型号的水笔,销售情况记录如下:设售出水笔数量为x(x是正整数),营业额为y
y与x的关系是
(x是正整数)长方形的长是20,宽为x,长方形的面积y与
x的关系是________________;圆的周长随着半径的变化而变化,写出周长C
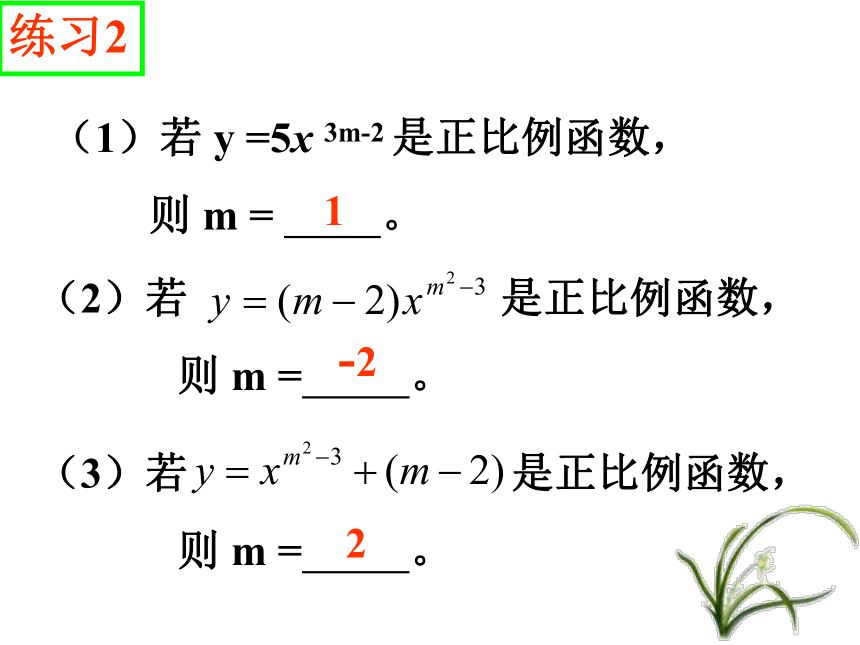
与半径r之间的函数关系式 (x是正整数)设售出水笔数量为x(x是正整数),营业额为y,y与x的关系是 一般地,如果变量x、y有关系y=kx(k≠0),那么称变量x、y成正比例。相应地,函数y=kx(k≠0),叫作 正比例函数。其中的常数k叫作比 例系数.下列函数中哪些是正比例函数?是正比例函数的说出比例系数(2)y = x+2练习1(1)y =2x(5)y=x2+1 (3)(4)(6)是是不是不是不是不是(1)若 y =5x 3m-2 是正比例函数,
则 m = 。(2)若 是正比例函数,
则 m = 。1-2(3)若 是正比例函数,
则 m = 。2练习2(2)若 是正比例函数,
则 m = 。例1已知正比例函数y=kx (k≠0),当x=-3时,y=6,
(1)求比例系数k,并写出这个正比例函数的关系式;4-10-22(1)解:把当x=-3,y=6代入y=kx中,得, 6=-3k 解得:k=-2∴函数关系式为y=-2x(2)填写下表解:(1)因为y是x的正比例函数,所以设 y=kx(k≠0)把 x =-4, y =2 代入上式,得2 = -4k解得(2)当 x=6 时, y = -3.已知y是x的正比例函数,且当x=-4时,y=2。(1)求y与x之间的函数解析式 (2)当x=6时,求函数y的值。例2已知y – 1与x+1成正比例,且当x= – 2时,y= – 1.当y= – 1时,求x的值 解:(1) 因为y – 1与x+1成正比例,所以设 y – 1=k(x+1) (k≠0).把x= – 2,y= – 1代入上式,得– 1 – 1= k(– 2+1)解得 k=2∴ y – 1=2(x+1)整理得:y=2x+3∵ y= – 1, ∴ – 1=2x+3解得 x= – 2所以x的值是– 2例3已知:y=y1+y2,y1与x成正比例,y2与x2成正比
例,当x=1时,y=6,当x=3时,y=8,求y关于x
的解析式。解:∵ y1与x成正比例, ∴y1=k1x(k1≠0)∵y2与x2成正比例,∴y2=k2x2(k2≠0)把x=1,y=6代入①中,得k1×1+k2×12=6∵y=y1+y2 ,∴y=k1x+k2x2 ①把x=3,y=8代入①中,得k1×3+k2×32=8解方程组 得例4 ∴y关于x的函数解析式为:已知△ABC的一边BC=8cm,当BC边上的高线从小到大变化时, △ABC的面积也随之变化。(1)写出△ABC的面积 y(cm2) 与高线 x(cm)的函数解析式,并指明它是什么函数;
(2)当x=7时,求出y的值。解:(1)∵(2)当x=7时,y=4×7=28即,这是正比例函数3∴又∵ BC=8(X>0)练习:已知:y= y1+ y2,y1与x成正比例,y2 与 x2 成正比例,当 x=1 时,y =6;当x=3时,y=6,求y关于x的解析式。略解:设 y1 = k1 x, (k1 ≠0),y2= k2 x2(k2 ≠0)
则 y = k1 x + k2x2由题意得 k1 + k2 = 6 3k1 +9k2 = 6∴ y = 8x -2x2小结:2、正比例函数的特征是什么?3、求正比例函数的解析式的四个步骤是什么?1、如何判定y和x是正比例关系?作业:B册21.3
一课一练:P53-54
同步:P61-63
y与x的关系是
(x是正整数)长方形的长是20,宽为x,长方形的面积y与
x的关系是________________;圆的周长随着半径的变化而变化,写出周长C
与半径r之间的函数关系式 (x是正整数)设售出水笔数量为x(x是正整数),营业额为y,y与x的关系是 一般地,如果变量x、y有关系y=kx(k≠0),那么称变量x、y成正比例。相应地,函数y=kx(k≠0),叫作 正比例函数。其中的常数k叫作比 例系数.下列函数中哪些是正比例函数?是正比例函数的说出比例系数(2)y = x+2练习1(1)y =2x(5)y=x2+1 (3)(4)(6)是是不是不是不是不是(1)若 y =5x 3m-2 是正比例函数,
则 m = 。(2)若 是正比例函数,
则 m = 。1-2(3)若 是正比例函数,
则 m = 。2练习2(2)若 是正比例函数,
则 m = 。例1已知正比例函数y=kx (k≠0),当x=-3时,y=6,
(1)求比例系数k,并写出这个正比例函数的关系式;4-10-22(1)解:把当x=-3,y=6代入y=kx中,得, 6=-3k 解得:k=-2∴函数关系式为y=-2x(2)填写下表解:(1)因为y是x的正比例函数,所以设 y=kx(k≠0)把 x =-4, y =2 代入上式,得2 = -4k解得(2)当 x=6 时, y = -3.已知y是x的正比例函数,且当x=-4时,y=2。(1)求y与x之间的函数解析式 (2)当x=6时,求函数y的值。例2已知y – 1与x+1成正比例,且当x= – 2时,y= – 1.当y= – 1时,求x的值 解:(1) 因为y – 1与x+1成正比例,所以设 y – 1=k(x+1) (k≠0).把x= – 2,y= – 1代入上式,得– 1 – 1= k(– 2+1)解得 k=2∴ y – 1=2(x+1)整理得:y=2x+3∵ y= – 1, ∴ – 1=2x+3解得 x= – 2所以x的值是– 2例3已知:y=y1+y2,y1与x成正比例,y2与x2成正比
例,当x=1时,y=6,当x=3时,y=8,求y关于x
的解析式。解:∵ y1与x成正比例, ∴y1=k1x(k1≠0)∵y2与x2成正比例,∴y2=k2x2(k2≠0)把x=1,y=6代入①中,得k1×1+k2×12=6∵y=y1+y2 ,∴y=k1x+k2x2 ①把x=3,y=8代入①中,得k1×3+k2×32=8解方程组 得例4 ∴y关于x的函数解析式为:已知△ABC的一边BC=8cm,当BC边上的高线从小到大变化时, △ABC的面积也随之变化。(1)写出△ABC的面积 y(cm2) 与高线 x(cm)的函数解析式,并指明它是什么函数;
(2)当x=7时,求出y的值。解:(1)∵(2)当x=7时,y=4×7=28即,这是正比例函数3∴又∵ BC=8(X>0)练习:已知:y= y1+ y2,y1与x成正比例,y2 与 x2 成正比例,当 x=1 时,y =6;当x=3时,y=6,求y关于x的解析式。略解:设 y1 = k1 x, (k1 ≠0),y2= k2 x2(k2 ≠0)
则 y = k1 x + k2x2由题意得 k1 + k2 = 6 3k1 +9k2 = 6∴ y = 8x -2x2小结:2、正比例函数的特征是什么?3、求正比例函数的解析式的四个步骤是什么?1、如何判定y和x是正比例关系?作业:B册21.3
一课一练:P53-54
同步:P61-63
