25.1 锐角的三角比的意义

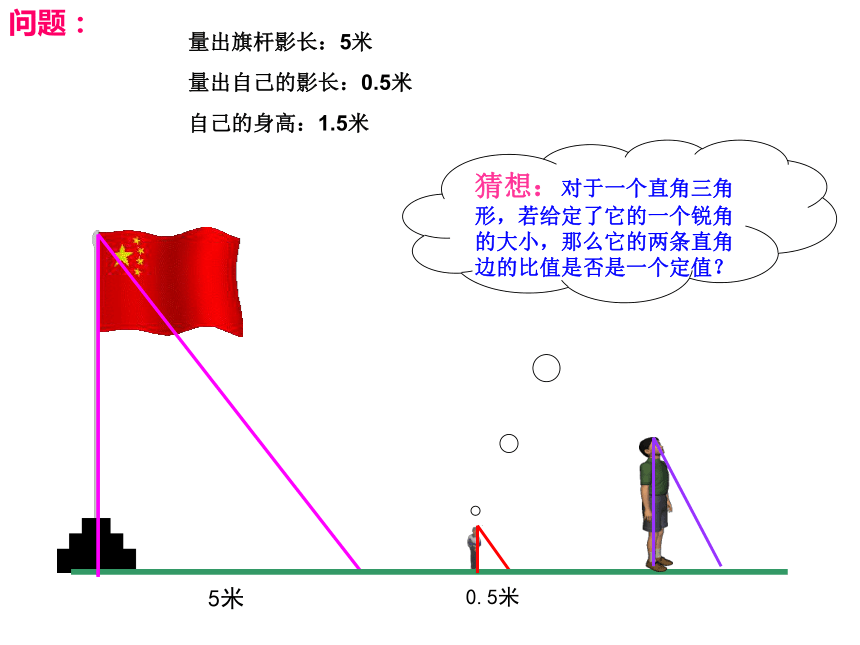
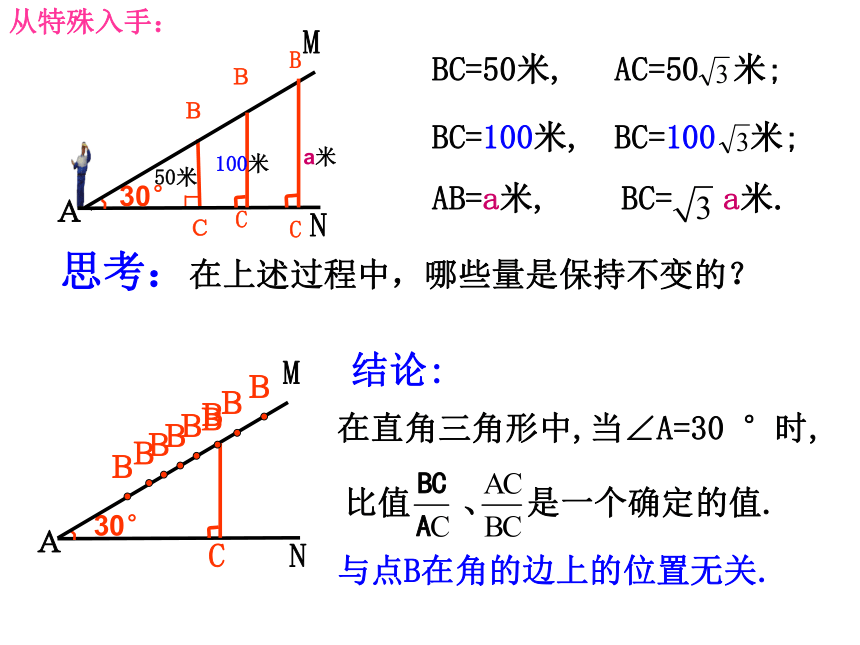
课件17张PPT。25.1(1)锐角三角比的意义延吉初级 秦娟问题：猜想：对于一个直角三角形，若给定了它的一个锐角的大小，那么它的两条直角边的比值是否是一个定值？自己的身高：1.5米Ｂ50米Ａ30°NMBC=50米,BC=100米,AB=a米,BC= a米.a米思考：在上述过程中，哪些量是保持不变的？ 与点B在角的边上的位置无关.100米AC=50 米;BC=100 米;从特殊入手：角度不变，比值不变.
角度改变，比值改变.
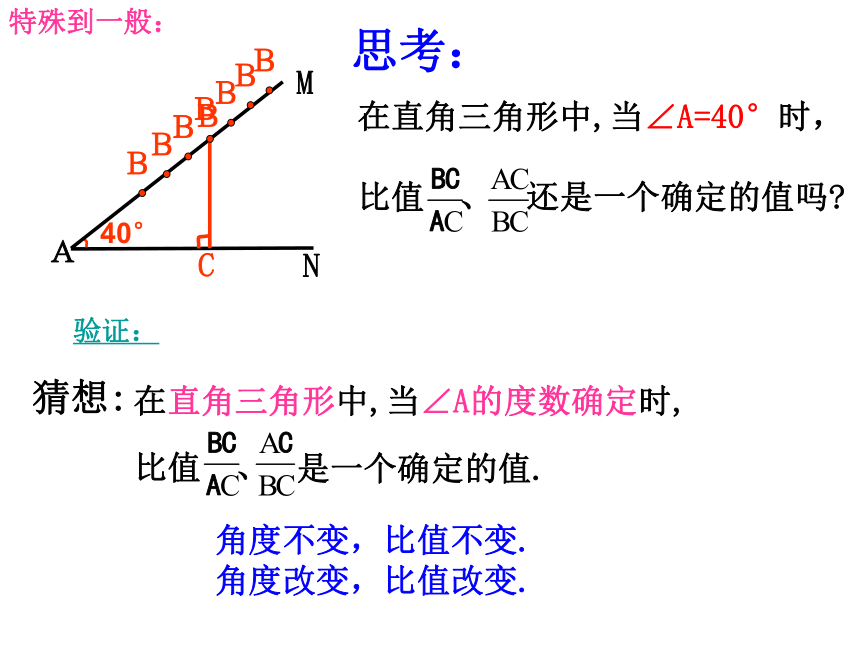
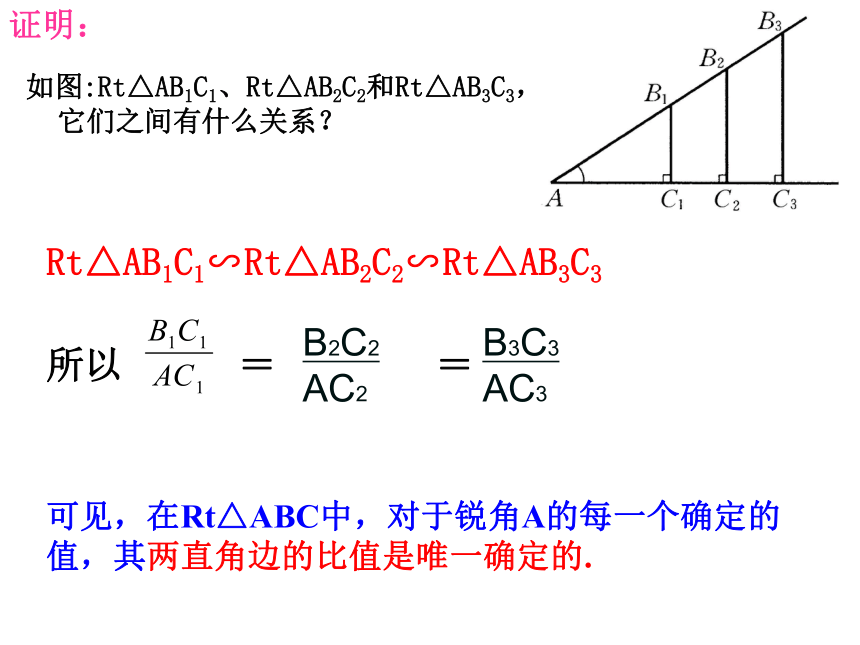
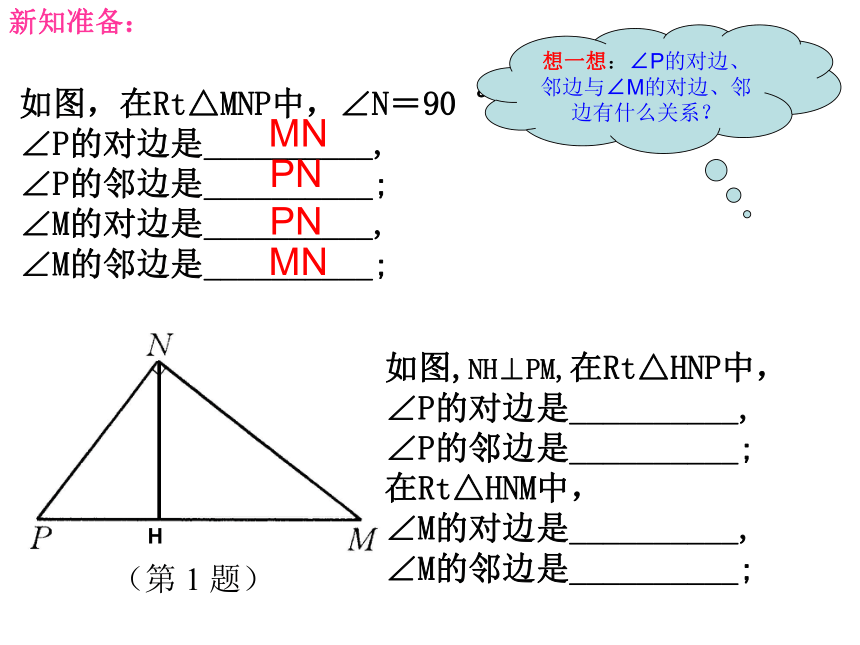
Ａ40°NM验证：特殊到一般：如图:Rt△AB1C1、Rt△AB2C2和Rt△AB3C3，它们之间有什么关系？Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3可见，在Rt△ABC中，对于锐角A的每一个确定的值，其两直角边的比值是唯一确定的.证明：如图，在Rt△MNP中，∠N＝90゜.∠P的对边是__________,∠P的邻边是__________;∠M的对边是__________,∠M的邻边是__________;想一想：∠P的对边、邻边与∠M的对边、邻边有什么关系？新知准备：如图,NH⊥PM,在Rt△HNP中，∠P的对边是__________,∠P的邻边是__________;在Rt△HNM中， ∠M的对边是__________,∠M的邻边是__________;在Rt△ABC中，∠C=90°， 锐角三角比的定义:
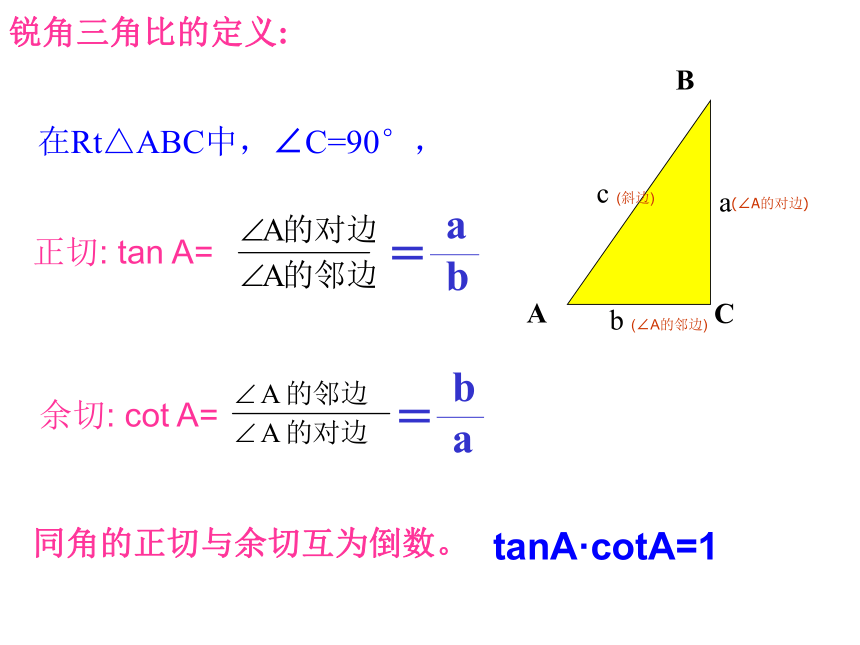
正切: tan A= 余切: cot A=tanA·cotA=1同角的正切与余切互为倒数。注意:1.锐角的正切和余切是在直角三角形中定义的。
2.tanA和cotA是一个完整的符号。
3.tanA和cotA是一个比值。
4.锐角的正切和余切由角的大小唯一确定,而与边的长短无关。10m(2)(2).如图 (2)( ). 真真假假:(3).如图 (2)( ). tanBAC =(1)5m小试牛刀：1、在Rt△ABC中,∠C=90o,AC=4,BC=3, 　　　　　
则tanA= tanB = 。
cotA= cotB = 。2、在Rt△ABC中,∠ACB=90o,CD⊥AB, 　　　　　
则tanA= ;tanB
tanB = 。
(写出尽可能多的线段比）3、如图在Rt⊿ABC中，∠C=90°，D、E在B上， AC=4，BD=5，DE=2，EC=3， ∠ABC=α，∠ADC=β，∠AEC=γ。 则tanα= cotβ= tanγ= 。 例： 在Rt△ABC中,∠C=90°,AB=17,BC=15, 　　　　　
求tanA和cotA的值。17例题讲解：3、⑴在如图所示的格点图中，请求出锐角α的三角函数值;
⑶以射线AB为始边任意作锐角∠DAB，并求出它的正切值；请组内比较，谁画出的锐角的正切值最大？⑵如图，请你以射线AB为始边作锐角∠CAB，使它的正切值为 ;我来画画：你能说说tanA的取值范围吗？ 求一个角的正切值，除了用定义直接求外，还可以转化为求和它相等角的正切值。如图, ∠ACB=90°，
CD⊥AB. CD=4，BD=2，
求：tanA拓展练习经历了一个探究过程：学习了一个重要概念：在本节课中,我们……体现了一种数学思想：
体验到一种学习方法：特殊到一般数形结合反思提炼正切余切靠直角,
比值跟着角度变.
“切”从零至无限,
定义符号记心间.作业：
练习册25.1(1)
堂堂练25.1(1)
归纳小结，反思提高sinAcosAtanA∠A的正弦∠A的余弦∠A的正切00