15.2.2完全平方公式
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
15.2.2完全平方公式
教
案
嘉祥金屯镇中学
孙齐芳
15.2.2 完全平方公式
教学目标
(一)教学知识点
1.完全平方公式的推导及其应用.
2.完全平方公式的几何解释.
(二)能力训练要求
1.经历探索完全平方公式的过程,进一步发展符号感和推理能力.
2.重视学生对算理的理解,有意识地培养学生的思维条理性和表达能力.
(三)情感与价值观要求
在灵活应用公式的过程中激发学生学习数学的兴趣,培养创新能力和探索精神.
重点:完全平方公式的推导过程、结构特点、几何解释,灵活应用.
难点 : 理解完全平方公式的结构特征并能灵活应用公式进行计算.
教学准备
教师:多媒体课件 边长分别为a,b的两个正方形纸片和两个一边为a,一边为b的矩形纸片 。
学生:边长分别为a,b的两个正方形纸片和两个一边为a,一边为b的矩形纸片 。
教学过程
1、 探究
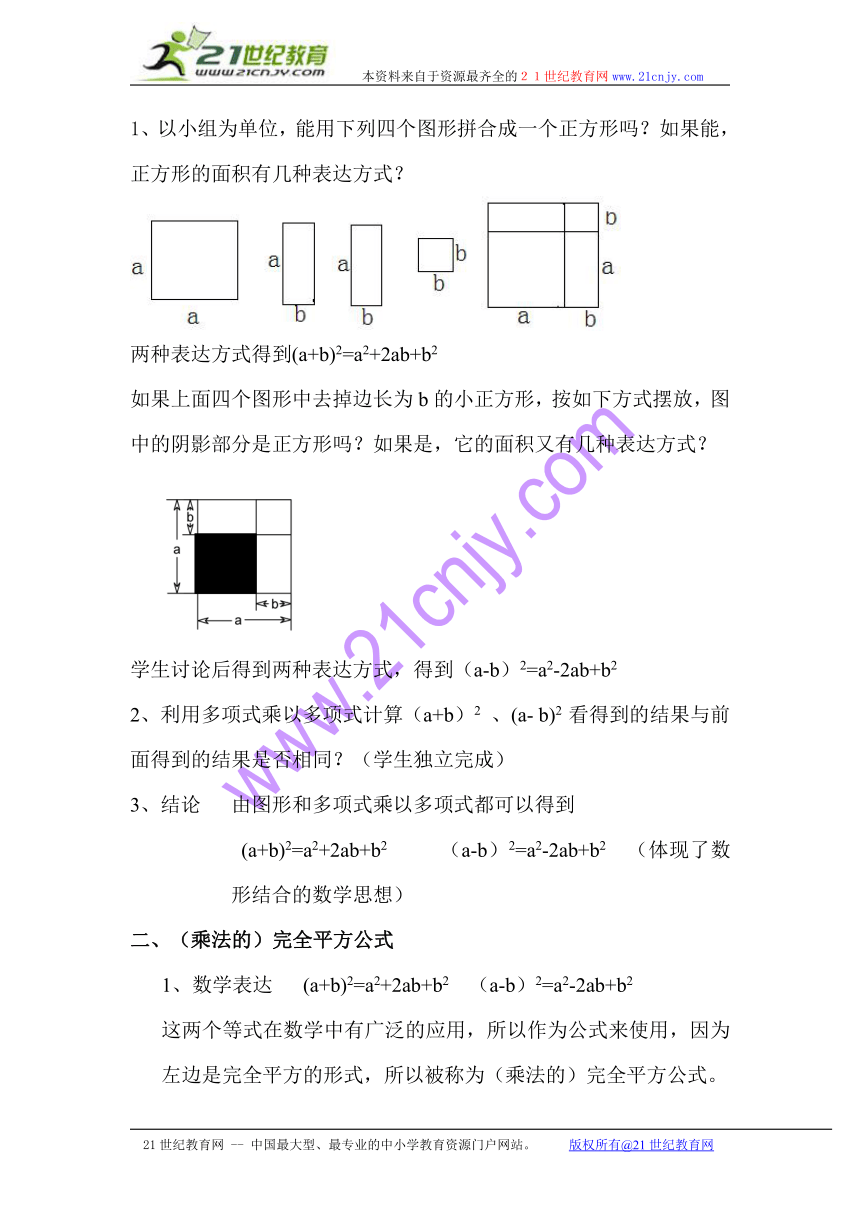
1、以小组为单位,能用下列四个图形拼合成一个正方形吗?如果能,正方形的面积有几种表达方式?
两种表达方式得到(a+b)2=a2+2ab+b2
如果上面四个图形中去掉边长为b的小正方形,按如下方式摆放,图中的阴影部分是正方形吗?如果是,它的面积又有几种表达方式?
学生讨论后得到两种表达方式,得到(a-b)2=a2-2ab+b2
2、利用多项式乘以多项式计算(a+b)2 、(a- b)2 看得到的结果与前面得到的结果是否相同?(学生独立完成)
3、结论 由图形和多项式乘以多项式都可以得到
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2 (体现了数形结合的数学思想)
二、(乘法的)完全平方公式
1、数学表达 (a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
这两个等式在数学中有广泛的应用,所以作为公式来使用,因为左边是完全平方的形式,所以被称为(乘法的)完全平方公式。
2、公式的结构特征 (由学生讨论后得出)
(1)左边是一个二项式的完全平方
(2)右边的积有三项,其中两项是左边二项式中两项的平方和,另一项是左边二项式中两项乘积的两倍
(3)字母a,b可以代表数字,也可以代表单项式、多项式。
3、语言叙述
两个数的和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍。
简记为 首平方加尾平方,首尾两倍在中央,加减看前方。
二、公式的应用
1、判断下列式子是否正确,若不正确,加以改正。
①(a+b)2=a2+b2
② (x-y)2=x2-y2
2、例题精析
例:用完全平方公式计算
(1)(4m+n)2 (2) (y- )2
析:首先选准公式,找准对应的a,b, 然后套入公式准确的计算。
解:(1)(4m+n)2 =(4m)2+2·(4m)·n+n2
=16m2+8mn+n2
思考:此题还有其他方法吗?(体会完全平方公式的简便)
学生共同完成(2)
3、提高训练
(1)用完全平方公式计算
①(y+6)2
② (-2x+5)2
鼓励学生用多种方法解题,训练学生思维的灵活性。
思考:你怎样计算992吗?1022呢?
总结:在使用(乘法的)完全平方公式时应该注意什么?(同位交流)
4、能力提升
计算(-x-y)2
学生先独立完成,然后小组交流解题方法。
(-x-y)2 =〔-(x+y)〕2=(x+y)2
(-x-y)2 =〔(-x)+(-y)〕2
三、探究添括号的法则
在上题中我们添加了括号,在以前我们学习过去括号的法则,回忆去括号的法则。
在等号右边的括号内填上适当的项
(1) a+b-c=a+( )
(2) a-b+c=a- ( )
(3) a-b-c=a- ( )
仿照去括号的法则,同位交流得到添括号的法则
添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号。
遇“加”不变,遇“减”都变
四、开拓创新
你能计算(a-b+1)2吗?
五、课堂小结
在这节课中你学到了什么?有什么感想?
在数学学习的过程中应该注意什么?
教师寄语:
扎实的基础知识,灵活的思维方法,规范的解题步骤是学好数学的法宝。
六、作业
1、课本p156 2、5、6
2、计算(x+2y-3)(x-2y+3)
3、已知:a+b=5,ab=-6,求下列各式的值
(1)(a+b)2 (2)a2+b2
板书设计
15.2.2完全平方公式
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
例 (1)(4m+n)2
解:原式 =(4m)2+2 (4m) n+n2
=16m2+8mn+n2
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
15.2.2完全平方公式
教
案
嘉祥金屯镇中学
孙齐芳
15.2.2 完全平方公式
教学目标
(一)教学知识点
1.完全平方公式的推导及其应用.
2.完全平方公式的几何解释.
(二)能力训练要求
1.经历探索完全平方公式的过程,进一步发展符号感和推理能力.
2.重视学生对算理的理解,有意识地培养学生的思维条理性和表达能力.
(三)情感与价值观要求
在灵活应用公式的过程中激发学生学习数学的兴趣,培养创新能力和探索精神.
重点:完全平方公式的推导过程、结构特点、几何解释,灵活应用.
难点 : 理解完全平方公式的结构特征并能灵活应用公式进行计算.
教学准备
教师:多媒体课件 边长分别为a,b的两个正方形纸片和两个一边为a,一边为b的矩形纸片 。
学生:边长分别为a,b的两个正方形纸片和两个一边为a,一边为b的矩形纸片 。
教学过程
1、 探究
1、以小组为单位,能用下列四个图形拼合成一个正方形吗?如果能,正方形的面积有几种表达方式?
两种表达方式得到(a+b)2=a2+2ab+b2
如果上面四个图形中去掉边长为b的小正方形,按如下方式摆放,图中的阴影部分是正方形吗?如果是,它的面积又有几种表达方式?
学生讨论后得到两种表达方式,得到(a-b)2=a2-2ab+b2
2、利用多项式乘以多项式计算(a+b)2 、(a- b)2 看得到的结果与前面得到的结果是否相同?(学生独立完成)
3、结论 由图形和多项式乘以多项式都可以得到
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2 (体现了数形结合的数学思想)
二、(乘法的)完全平方公式
1、数学表达 (a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
这两个等式在数学中有广泛的应用,所以作为公式来使用,因为左边是完全平方的形式,所以被称为(乘法的)完全平方公式。
2、公式的结构特征 (由学生讨论后得出)
(1)左边是一个二项式的完全平方
(2)右边的积有三项,其中两项是左边二项式中两项的平方和,另一项是左边二项式中两项乘积的两倍
(3)字母a,b可以代表数字,也可以代表单项式、多项式。
3、语言叙述
两个数的和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍。
简记为 首平方加尾平方,首尾两倍在中央,加减看前方。
二、公式的应用
1、判断下列式子是否正确,若不正确,加以改正。
①(a+b)2=a2+b2
② (x-y)2=x2-y2
2、例题精析
例:用完全平方公式计算
(1)(4m+n)2 (2) (y- )2
析:首先选准公式,找准对应的a,b, 然后套入公式准确的计算。
解:(1)(4m+n)2 =(4m)2+2·(4m)·n+n2
=16m2+8mn+n2
思考:此题还有其他方法吗?(体会完全平方公式的简便)
学生共同完成(2)
3、提高训练
(1)用完全平方公式计算
①(y+6)2
② (-2x+5)2
鼓励学生用多种方法解题,训练学生思维的灵活性。
思考:你怎样计算992吗?1022呢?
总结:在使用(乘法的)完全平方公式时应该注意什么?(同位交流)
4、能力提升
计算(-x-y)2
学生先独立完成,然后小组交流解题方法。
(-x-y)2 =〔-(x+y)〕2=(x+y)2
(-x-y)2 =〔(-x)+(-y)〕2
三、探究添括号的法则
在上题中我们添加了括号,在以前我们学习过去括号的法则,回忆去括号的法则。
在等号右边的括号内填上适当的项
(1) a+b-c=a+( )
(2) a-b+c=a- ( )
(3) a-b-c=a- ( )
仿照去括号的法则,同位交流得到添括号的法则
添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号。
遇“加”不变,遇“减”都变
四、开拓创新
你能计算(a-b+1)2吗?
五、课堂小结
在这节课中你学到了什么?有什么感想?
在数学学习的过程中应该注意什么?
教师寄语:
扎实的基础知识,灵活的思维方法,规范的解题步骤是学好数学的法宝。
六、作业
1、课本p156 2、5、6
2、计算(x+2y-3)(x-2y+3)
3、已知:a+b=5,ab=-6,求下列各式的值
(1)(a+b)2 (2)a2+b2
板书设计
15.2.2完全平方公式
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
例 (1)(4m+n)2
解:原式 =(4m)2+2 (4m) n+n2
=16m2+8mn+n2
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
