初三上学期数学期末质量检测试题
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
初三数学期末质量检测试题
(时间90分钟,满分120分)
题号 一 二 三 总分
得分 21 22 23 24 25 26
一、选择题(每题3分,共30分)
1、下列方程中,一元二次方程是( )
A. B.=0 C. D.
2、下列说法不正确的是( )
A.中心对称图形一定是旋转对称图形
B.轴对称图形一定是中心对称图形
C.在成中心对称的两个图形中,连结对称点的线段都被对称中心平分
D.在平移过程中,对应点所连的线段也可能在一条直线上
3、下列命题:
(1)等边三角形是中心对称图形;
(2)一组对边平行,另一组对边相等的四边形是平行四边形;
(3)两条对角线互相垂直的矩形是正方形;
(4)两条对角线互相垂直的四边形是菱形.
其中正确命题的个数为( )
A.1个 B.2个 C.3个 D.4个
4、用配方法解下列方程,其中应该左右两边同时加上4的是( )
A. B. C. D.
5、如图所示,已知△ABC的内切圆O与各边相切于D、E、F,那么点O是△DEF的( )
A.三条中线的交点 B.三条高的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
6、方程的解的情况是( )
A有两个不相等的实数根 B. 没有实数根 C. 有两个相等的实数根 D.有一个实数根
第5题图 第7题图 第10题图
7、如图,图形旋转一定角度后能与自身重合,则旋转的角度可能是( )
A.300 B.600 C.900 D.1200
8、某超市一月份的营业额为200万元,一月、二月、三月的营业额共1000万元,如果平均每月增长率为,则由题意列方程应为( )
A. B.
C. D.
9、半径分别为1cm 和2cm 的两圆外切,那么与这两圆都相切且半径为3cm 的圆的个数有( )
A.5个 B.4个 C.3个 D.2个
10、如图一个圆环的面积为9π,大圆的弦AB切小圆于点C,则弦AB的长为( )
A.9 B.6 C.3 D.18
二、填空题(每题3分,共30分)
11、若方程有两个相等的实数根,则= ,两个根分别为 。
12、如图,在平行四边形ABCD中,∠A的平分线交BC于点E,若AB=10厘米,AD=14 厘米, 则
BE=___ _,EC=______ __.
第12题 第15题图 第17题图
13、若一个三角形的三边长均满足方程,则此三角形的周长为___ _____。
14、已知三边长为3、4、6的ΔABC的内切圆半径为r,则ΔABC的面积= 。
15、如图,把三角形△ABC绕着点C顺时针旋转35°,得到△A'B'C,A'B'交AC于点D,若∠A'DC=90°,则∠A的度数是_____ ___。
16、在Rt△ABC中,∠C=90°,AC=5,BC=12.若以C为圆心,R为半径作的圆与斜边AB没有公共点,则R的取值范围是
17、如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于E,BE=3厘米,AB=6厘米,DF=5厘米, 则平行四边形ABCD的周长为___ ___厘米.
18、⊙O的直径为10,弦AB=6,P是AB上一动点,则OP的取值范围是 。
19、某商品两次价格上调后,单位价格从5元变为6.05元,则平均每次调价的百分率
是 。
20、⊙O的半径OA=1,弦AB,AC的长分别是,则∠BAC= 。
三、解答题(共60分)
21、(12分)(1)2 (2)
(3) (4)
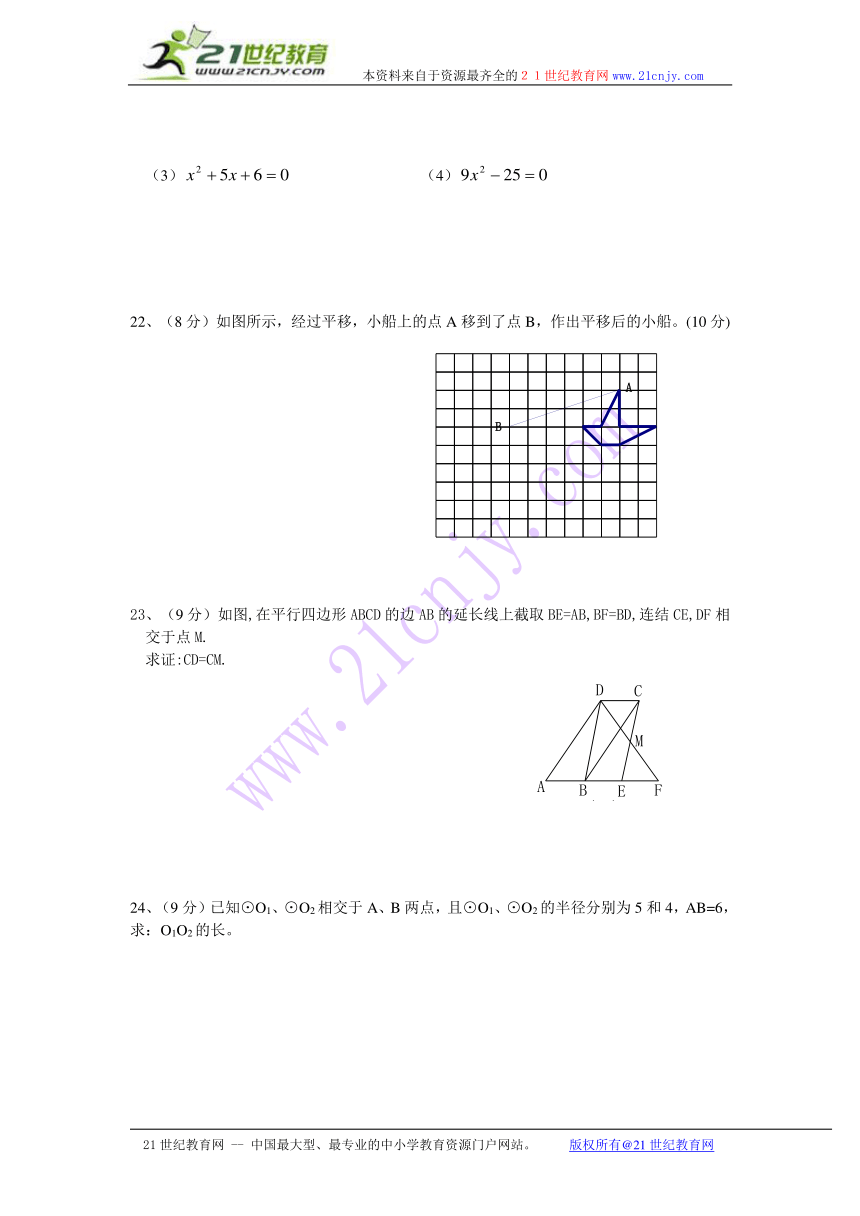
22、(8分)如图所示,经过平移,小船上的点A移到了点B,作出平移后的小船。(10分)
23、(9分)如图,在平行四边形ABCD的边AB的延长线上截取BE=AB,BF=BD,连结CE,DF相交于点M.
求证:CD=CM.
24、(9分)已知⊙O1、⊙O2相交于A、B两点,且⊙O1、⊙O2的半径分别为5和4,AB=6,
求:O1O2的长。
25、(10分)百货商店服装柜在销售中发现,某品牌童装平均每天可售出20件,每件盈利40元。为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存。经市场调查发现,如果每件童装降价1元,那么平均每天就可多售出2件,要想平均每天销售童装盈利1200元,那么每件童装应降价多少元?
26、(12分)如图,已知AB是⊙O的直径,⊙O经过BC的中点D,是DE⊥BC,垂足为E。
(1)求证:DE是⊙O的切线;
(2)若∠C=30°,CD=10cm,求⊙O的半径。
《初三数学期末质量检测试卷》答案
1、C 2、B 3、A 4、C 5、D 6、A 7、C 8、D 9、A 10、B
11、 12、10厘米,4厘米 13、10 14、
15、55° 16、 17、32 18、4≤OP≤5 19、10% 20、15°或75°
21、⑴ ⑵⑶⑷
22、如右图
23、解:在△ABD与△BEC中,
∵AD=BC,AB=BE,∠A=∠CBE,
∴把△BEC 沿BA方向,平移距离
AB后可与△ABD完全重合.
∴∠ABD=∠BEC,
∴BD∥EC(同位角相等,二直线平行).
∴∠BDM=∠CMD,又DC∥AE,
∴∠F=∠CDM,
又∵BD=BF,∴∠F=∠BDF,
∴∠CDM=∠CMD,∴CM=CD.
24、解:连结O1A,O2A交O1O2与点C,由题意知,O1O2垂直平分AB,
∵AB=6,∴AC=3
在Rt△O1AC中,AC=3,O1A=5
∴O1C=
在Rt△O2AC中,AC=3,O2A=4
∴O2C=
当O1O2位于公共弦的两侧时,O1O2=
当O1O2位于公共弦的同侧时,O1O2=
∴O1O2的长为或。
25、解:设每件童装应降x元,由题意得:
(40-x)(20+2x)=1200
解得:x1=20 x2=10(舍)
因为减少库存,扩大销售量,所以x2=10不符合题意,应舍去
所以x=20
答:每件童装应降价20元。
26、⑴证明:连结BD,OD
∵AB为直径
∴∠ADB=90°
即BD⊥AC
∵D为AC的中点
∴AD=DC
∴AB=BC
∴∠A=∠C
又∵OA=OD
∴∠A=∠ODA
∴∠C=∠ODA
∴OD∥BC
又∵DE⊥BC
∴DE⊥OD
∴DE是⊙O的切线
⑵∵DC=10,DC=AD
∴AD=10
又∵∠A=∠C,∠C=30°
∴∠A=30°
在Rt△ADB中,∵
∴
∴AO=
∴⊙O的半径为。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
初三数学期末质量检测试题
(时间90分钟,满分120分)
题号 一 二 三 总分
得分 21 22 23 24 25 26
一、选择题(每题3分,共30分)
1、下列方程中,一元二次方程是( )
A. B.=0 C. D.
2、下列说法不正确的是( )
A.中心对称图形一定是旋转对称图形
B.轴对称图形一定是中心对称图形
C.在成中心对称的两个图形中,连结对称点的线段都被对称中心平分
D.在平移过程中,对应点所连的线段也可能在一条直线上
3、下列命题:
(1)等边三角形是中心对称图形;
(2)一组对边平行,另一组对边相等的四边形是平行四边形;
(3)两条对角线互相垂直的矩形是正方形;
(4)两条对角线互相垂直的四边形是菱形.
其中正确命题的个数为( )
A.1个 B.2个 C.3个 D.4个
4、用配方法解下列方程,其中应该左右两边同时加上4的是( )
A. B. C. D.
5、如图所示,已知△ABC的内切圆O与各边相切于D、E、F,那么点O是△DEF的( )
A.三条中线的交点 B.三条高的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
6、方程的解的情况是( )
A有两个不相等的实数根 B. 没有实数根 C. 有两个相等的实数根 D.有一个实数根
第5题图 第7题图 第10题图
7、如图,图形旋转一定角度后能与自身重合,则旋转的角度可能是( )
A.300 B.600 C.900 D.1200
8、某超市一月份的营业额为200万元,一月、二月、三月的营业额共1000万元,如果平均每月增长率为,则由题意列方程应为( )
A. B.
C. D.
9、半径分别为1cm 和2cm 的两圆外切,那么与这两圆都相切且半径为3cm 的圆的个数有( )
A.5个 B.4个 C.3个 D.2个
10、如图一个圆环的面积为9π,大圆的弦AB切小圆于点C,则弦AB的长为( )
A.9 B.6 C.3 D.18
二、填空题(每题3分,共30分)
11、若方程有两个相等的实数根,则= ,两个根分别为 。
12、如图,在平行四边形ABCD中,∠A的平分线交BC于点E,若AB=10厘米,AD=14 厘米, 则
BE=___ _,EC=______ __.
第12题 第15题图 第17题图
13、若一个三角形的三边长均满足方程,则此三角形的周长为___ _____。
14、已知三边长为3、4、6的ΔABC的内切圆半径为r,则ΔABC的面积= 。
15、如图,把三角形△ABC绕着点C顺时针旋转35°,得到△A'B'C,A'B'交AC于点D,若∠A'DC=90°,则∠A的度数是_____ ___。
16、在Rt△ABC中,∠C=90°,AC=5,BC=12.若以C为圆心,R为半径作的圆与斜边AB没有公共点,则R的取值范围是
17、如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于E,BE=3厘米,AB=6厘米,DF=5厘米, 则平行四边形ABCD的周长为___ ___厘米.
18、⊙O的直径为10,弦AB=6,P是AB上一动点,则OP的取值范围是 。
19、某商品两次价格上调后,单位价格从5元变为6.05元,则平均每次调价的百分率
是 。
20、⊙O的半径OA=1,弦AB,AC的长分别是,则∠BAC= 。
三、解答题(共60分)
21、(12分)(1)2 (2)
(3) (4)
22、(8分)如图所示,经过平移,小船上的点A移到了点B,作出平移后的小船。(10分)
23、(9分)如图,在平行四边形ABCD的边AB的延长线上截取BE=AB,BF=BD,连结CE,DF相交于点M.
求证:CD=CM.
24、(9分)已知⊙O1、⊙O2相交于A、B两点,且⊙O1、⊙O2的半径分别为5和4,AB=6,
求:O1O2的长。
25、(10分)百货商店服装柜在销售中发现,某品牌童装平均每天可售出20件,每件盈利40元。为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存。经市场调查发现,如果每件童装降价1元,那么平均每天就可多售出2件,要想平均每天销售童装盈利1200元,那么每件童装应降价多少元?
26、(12分)如图,已知AB是⊙O的直径,⊙O经过BC的中点D,是DE⊥BC,垂足为E。
(1)求证:DE是⊙O的切线;
(2)若∠C=30°,CD=10cm,求⊙O的半径。
《初三数学期末质量检测试卷》答案
1、C 2、B 3、A 4、C 5、D 6、A 7、C 8、D 9、A 10、B
11、 12、10厘米,4厘米 13、10 14、
15、55° 16、 17、32 18、4≤OP≤5 19、10% 20、15°或75°
21、⑴ ⑵⑶⑷
22、如右图
23、解:在△ABD与△BEC中,
∵AD=BC,AB=BE,∠A=∠CBE,
∴把△BEC 沿BA方向,平移距离
AB后可与△ABD完全重合.
∴∠ABD=∠BEC,
∴BD∥EC(同位角相等,二直线平行).
∴∠BDM=∠CMD,又DC∥AE,
∴∠F=∠CDM,
又∵BD=BF,∴∠F=∠BDF,
∴∠CDM=∠CMD,∴CM=CD.
24、解:连结O1A,O2A交O1O2与点C,由题意知,O1O2垂直平分AB,
∵AB=6,∴AC=3
在Rt△O1AC中,AC=3,O1A=5
∴O1C=
在Rt△O2AC中,AC=3,O2A=4
∴O2C=
当O1O2位于公共弦的两侧时,O1O2=
当O1O2位于公共弦的同侧时,O1O2=
∴O1O2的长为或。
25、解:设每件童装应降x元,由题意得:
(40-x)(20+2x)=1200
解得:x1=20 x2=10(舍)
因为减少库存,扩大销售量,所以x2=10不符合题意,应舍去
所以x=20
答:每件童装应降价20元。
26、⑴证明:连结BD,OD
∵AB为直径
∴∠ADB=90°
即BD⊥AC
∵D为AC的中点
∴AD=DC
∴AB=BC
∴∠A=∠C
又∵OA=OD
∴∠A=∠ODA
∴∠C=∠ODA
∴OD∥BC
又∵DE⊥BC
∴DE⊥OD
∴DE是⊙O的切线
⑵∵DC=10,DC=AD
∴AD=10
又∵∠A=∠C,∠C=30°
∴∠A=30°
在Rt△ADB中,∵
∴
∴AO=
∴⊙O的半径为。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
