高中数学人教新课标必修1:第二章 基本初等函数(ⅰ) 幂函数
文档属性
| 名称 | 高中数学人教新课标必修1:第二章 基本初等函数(ⅰ) 幂函数 |

|
|
| 格式 | rar | ||
| 文件大小 | 894.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-01-06 00:00:00 | ||
图片预览






文档简介
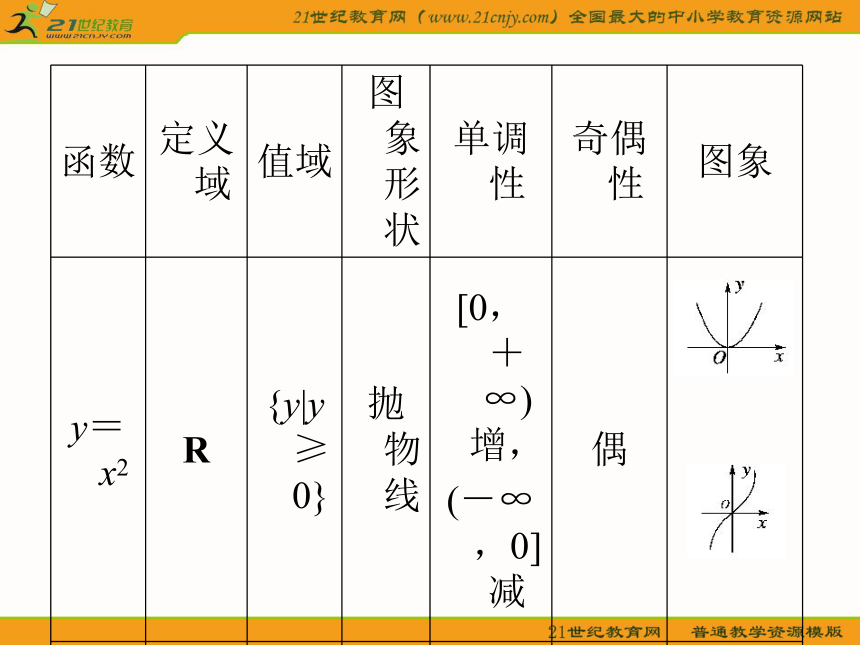
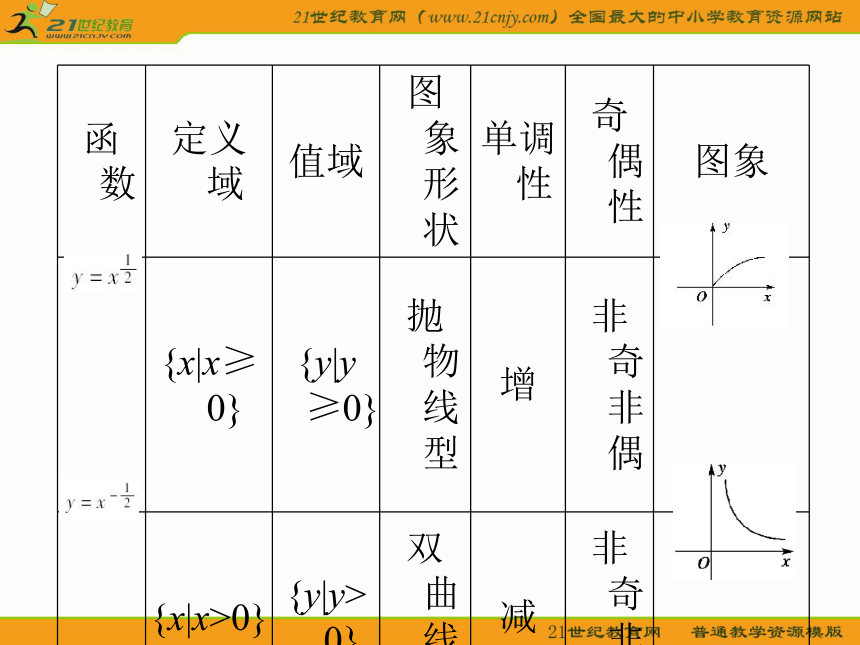
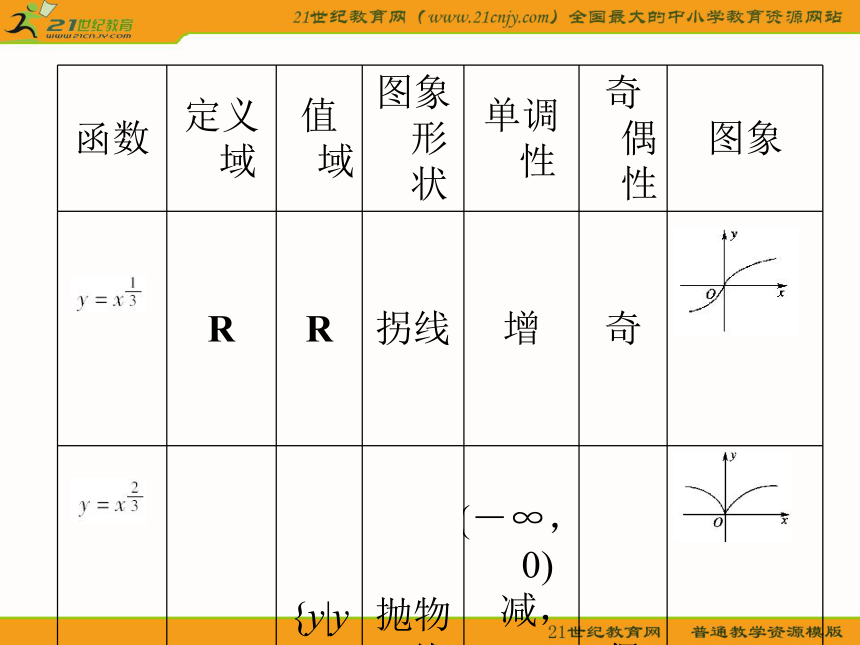
课件57张PPT。2.3 幂 函 数1.一般地形如 的函数叫做幂函数.y=xα(α为常数)函数的图象与性质列表如下:观察总结可知幂函数y=xα(α为常数)的性质:
(1)所有的幂函数在(0,+∞)上都有定义,并且图象都通过点(1,1);
(2)如果α>0,则幂函数的图象过原点,并且在区间[0,+∞)上为增函数;
(3)如果α<0,则幂函数在(0,+∞)上为减函数,在第一象限内,向上与y轴无限接近,向右与x轴无限接近.
(4)当α为奇数时,幂函数为奇函数,图象都过(-1,-1)点,当α为偶数时,幂函数为偶函数、图象都过(-1,1)点.本节重点:幂函数的概念、图象与性质.
本节难点:幂函数y=xα的图象随α取值不同的分布与变化规律.
[例1] 幂函数y=xm,y=xn,y=xp,y=xq的图象如图,则将m、n、p、q的大小关系用“<”连接起来结果是________.[解析] 过原点的指数α>0,不过原点的α<0,
∴n<0,
当x>1时,在直线y=x上方的α>1,下方的α<1,
∴p>1,0x>1时,指数越大,图象越高,∴m>q,
综上所述n[点评] x>1时,逆时针方向α依次增大,故n函数y=xa,y=xb,y=xc的图象如图所示,则实数a、b、c的大小关系为 ( )
A.cC.b[答案] A
总结评述:1.注意利用幂函数的性质比较幂值大小的方法步骤.
第一步,据指数分清正负;
第二步,正数区分大于1与小于1的,a>1,α>0时,aα>1;00时01,α<0时01;
第三步,构造幂函数应用幂函数单调性,特别注意含字母时,要注意底数不在同一单调区间内的情形.2.给定一组数值,比较大小的步骤.
第一步:区分正负.一种情形是幂函数或指数函数值即幂式确定符号;另一种情形是对数式确定符号,要根据各自的性质进行.
第二步:正数通常还要区分大于1还是小于1.
第三步:同底的幂,用指数函数单调性;同指数的幂用幂函数单调性;同底的对数用对数函数单调性.第四步:对于底数与指数均不相同的幂,或底数与真数均不相同的对数值大小的比较,通常是找一中间值过渡或化同底(化同指)、或放缩、有时作商(或作差)、或指对互化,对数式有时还用换底公式作变换等等.
[解析] (1)考察幂函数y=x1.5,在区间[0,+∞)上是单调增函数,
∵a+1>a,∴(a+1)1.5>a1.5.
[例3] 某农药厂今年生产农药8 000吨,计划5年后把产量提高到14 000吨,问平均每年需增长百分之几?
[解析] 设平均每年增长的百分率为x,则由题意得,8 000(1+x)5=14 000,答:平均每年需增长11.9%.
[例4] 幂函数y=(m2-m-1)xm2-2m-3当x∈(0,+∞)时为减函数,求实数m的值.
[解析] ∵y=(m2-m-1)xm2-2m-3为幂函数,
∴m2-m-1=1,
即(m-2)(m+1)=0,
∴m=2,或m=-1.
当m=-1时,m2-2m-3=0不满足题意,舍去.
当m=2时,m2-2m-3=-3满足题设条件,
∴m=2.
已知幂函数f(x)=xm2-2m-3(m∈Z)为偶函数,且在区间(0,+∞)上是减函数.
(1)求函数f(x);
(2)比较f(-2)与f(1)的大小.
[解析] (1)由题意m2-2m-3<0,
∴-1∵m∈Z,∴m=0,1,2,
∵f(x)为偶函数,∴m2-2m-3为偶数,
∴m=1,∴f(x)=x-4.(2)∵f(x)在(0,+∞)上单调递减,
∴f(1)>f(2)=f(-2).
[例5] 判断幂函数y=x3的单调性和奇偶性.
[分析] 函数单调性的判断:取值——作差——判断符号——下结论,函数奇偶性的判断:定义域——f(-x)与-f(x)、f(x)的关系——下结论.
[解析] ∵f(-x)=(-x)3=-x3=-f(x),
∴y=x3是奇函数.
解法一:∵α=3>0,∴f(x)在(0,+∞)上为增函数,
又∵f(x)为奇函数,∴f(x)在R上为增函数.
解法二:在(-∞,+∞)上任取x1,x2,设x2>x1,
[辨析] 错解忽视了3x-1>0,2+x>0的限制条件.一、选择题
1.下列函数中是幂函数的是 ( )
[答案] C2.下列结论中,正确的是 ( )
A.幂函数的图象都通过点(0,0),(1,1)
B.幂函数的图象可以出现在第四象限
[答案] C3.下列幂函数的值域错误的是 ( )
[答案] D
[答案] B[答案] A
[答案] A二、解答题
7.比较下列各组中三个值的大小,并说明理由:
(1)所有的幂函数在(0,+∞)上都有定义,并且图象都通过点(1,1);
(2)如果α>0,则幂函数的图象过原点,并且在区间[0,+∞)上为增函数;
(3)如果α<0,则幂函数在(0,+∞)上为减函数,在第一象限内,向上与y轴无限接近,向右与x轴无限接近.
(4)当α为奇数时,幂函数为奇函数,图象都过(-1,-1)点,当α为偶数时,幂函数为偶函数、图象都过(-1,1)点.本节重点:幂函数的概念、图象与性质.
本节难点:幂函数y=xα的图象随α取值不同的分布与变化规律.
[例1] 幂函数y=xm,y=xn,y=xp,y=xq的图象如图,则将m、n、p、q的大小关系用“<”连接起来结果是________.[解析] 过原点的指数α>0,不过原点的α<0,
∴n<0,
当x>1时,在直线y=x上方的α>1,下方的α<1,
∴p>1,0
综上所述n
A.c
总结评述:1.注意利用幂函数的性质比较幂值大小的方法步骤.
第一步,据指数分清正负;
第二步,正数区分大于1与小于1的,a>1,α>0时,aα>1;0
第三步,构造幂函数应用幂函数单调性,特别注意含字母时,要注意底数不在同一单调区间内的情形.2.给定一组数值,比较大小的步骤.
第一步:区分正负.一种情形是幂函数或指数函数值即幂式确定符号;另一种情形是对数式确定符号,要根据各自的性质进行.
第二步:正数通常还要区分大于1还是小于1.
第三步:同底的幂,用指数函数单调性;同指数的幂用幂函数单调性;同底的对数用对数函数单调性.第四步:对于底数与指数均不相同的幂,或底数与真数均不相同的对数值大小的比较,通常是找一中间值过渡或化同底(化同指)、或放缩、有时作商(或作差)、或指对互化,对数式有时还用换底公式作变换等等.
[解析] (1)考察幂函数y=x1.5,在区间[0,+∞)上是单调增函数,
∵a+1>a,∴(a+1)1.5>a1.5.
[例3] 某农药厂今年生产农药8 000吨,计划5年后把产量提高到14 000吨,问平均每年需增长百分之几?
[解析] 设平均每年增长的百分率为x,则由题意得,8 000(1+x)5=14 000,答:平均每年需增长11.9%.
[例4] 幂函数y=(m2-m-1)xm2-2m-3当x∈(0,+∞)时为减函数,求实数m的值.
[解析] ∵y=(m2-m-1)xm2-2m-3为幂函数,
∴m2-m-1=1,
即(m-2)(m+1)=0,
∴m=2,或m=-1.
当m=-1时,m2-2m-3=0不满足题意,舍去.
当m=2时,m2-2m-3=-3满足题设条件,
∴m=2.
已知幂函数f(x)=xm2-2m-3(m∈Z)为偶函数,且在区间(0,+∞)上是减函数.
(1)求函数f(x);
(2)比较f(-2)与f(1)的大小.
[解析] (1)由题意m2-2m-3<0,
∴-1
∵f(x)为偶函数,∴m2-2m-3为偶数,
∴m=1,∴f(x)=x-4.(2)∵f(x)在(0,+∞)上单调递减,
∴f(1)>f(2)=f(-2).
[例5] 判断幂函数y=x3的单调性和奇偶性.
[分析] 函数单调性的判断:取值——作差——判断符号——下结论,函数奇偶性的判断:定义域——f(-x)与-f(x)、f(x)的关系——下结论.
[解析] ∵f(-x)=(-x)3=-x3=-f(x),
∴y=x3是奇函数.
解法一:∵α=3>0,∴f(x)在(0,+∞)上为增函数,
又∵f(x)为奇函数,∴f(x)在R上为增函数.
解法二:在(-∞,+∞)上任取x1,x2,设x2>x1,
[辨析] 错解忽视了3x-1>0,2+x>0的限制条件.一、选择题
1.下列函数中是幂函数的是 ( )
[答案] C2.下列结论中,正确的是 ( )
A.幂函数的图象都通过点(0,0),(1,1)
B.幂函数的图象可以出现在第四象限
[答案] C3.下列幂函数的值域错误的是 ( )
[答案] D
[答案] B[答案] A
[答案] A二、解答题
7.比较下列各组中三个值的大小,并说明理由:
