高中数学人教新课标必修1:第二章 基本初等函数(ⅰ) 幂函数章末归纳总结
文档属性
| 名称 | 高中数学人教新课标必修1:第二章 基本初等函数(ⅰ) 幂函数章末归纳总结 |

|
|
| 格式 | rar | ||
| 文件大小 | 841.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-01-06 00:00:00 | ||
图片预览










文档简介
课件36张PPT。章末归纳总结
一、熟练掌握指数幂的定义、运算法则、公式和对数的定义、运算法则、公式是指对函数及其一切运算赖以施行的基础
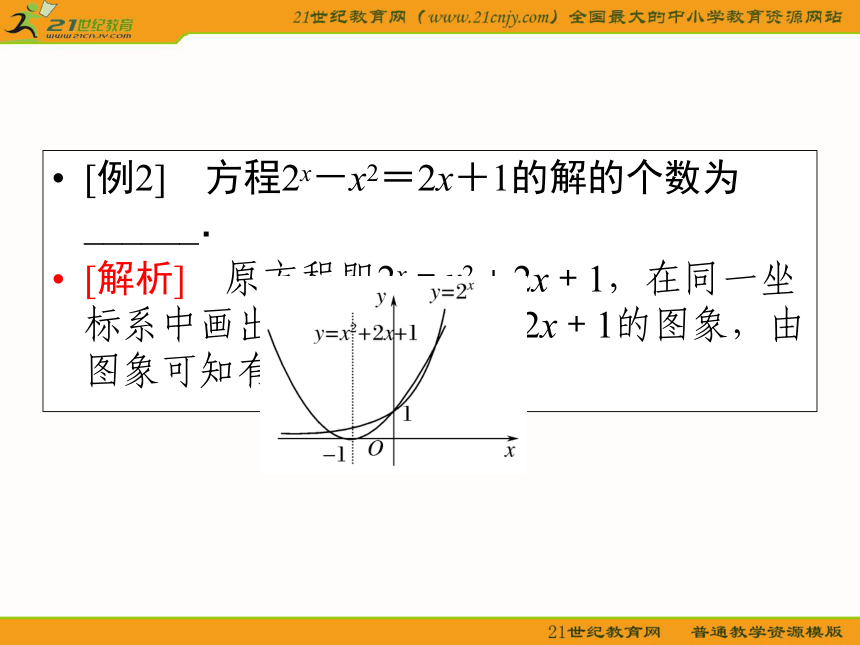
1.指数幂的定义与运算[答案] D[例2] 方程2x-x2=2x+1的解的个数为______.
[解析] 原方程即2x=x2+2x+1,在同一坐标系中画出y=2x,y=x2+2x+1的图象,由图象可知有3个交点.[例3] 0.32,log20.3,20.3这三数之间的大小顺序是( )
A.0.32<20.3B.0.32C.log20.3<0.32<20.3
D.log20.3<20.3<0.32
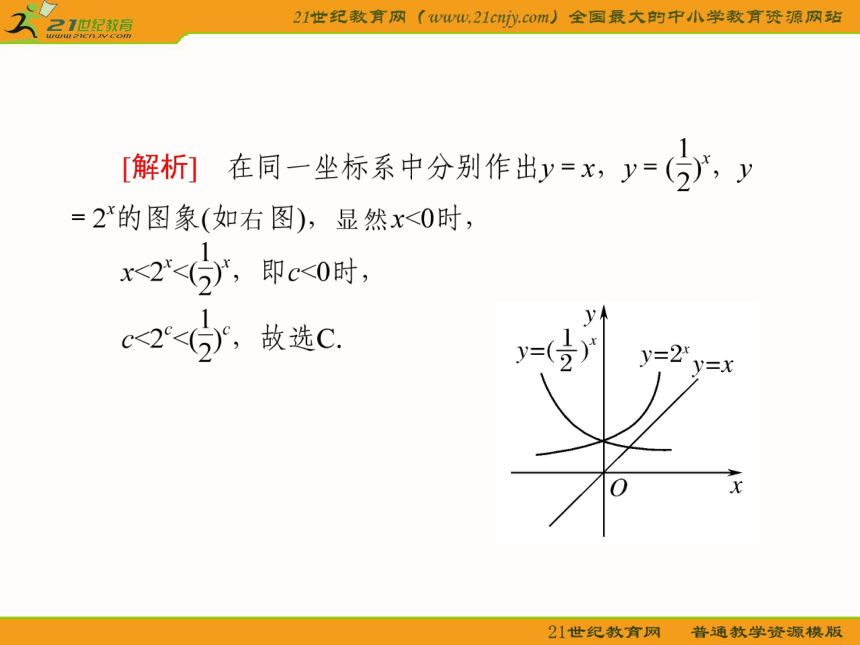
[分析] 可分别画出y=2x,y=log2x与y=x2的图象用图象来解决,也可以由幂、指、对函数值的分布规律解决.
[解析] 如图,
在同一坐标系中作出函数y=2x,y=x2及y=log2x的图象.
观察图象知当x=0.3时,log20.3<0.32<20.3.选C.[例4] 方程log3x+x=3的解所在的区间是( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,+∞)
[解析] 直接解方程是无法实现的,而借助于数形结合思想作出图象,则问题易于解决.
设y1=log3x,y2=-x+3,在同一坐标系中画出它们的图象(如下图)观察可排除A,D.其交点P的横坐标应在(1,3)内.
又x=2时,y1=log32<1,
而y2=-x+3=1,且知y1是增函数,y2是减函数,所以交点P的横坐标应在(2,3)内,∴选C.[例5] 设x∈(0,1)时,函数y=xp的图象在直线y=x的上方,则p的取值范围是________.
[解析] (1)当p>0时,根据题意p<1,∴0(2)当p=0时,函数为y=1(x≠0),符合题意.
(3)当p<0时,在(0,+∞)上过(1,1)点,函数为减函数,符合题意.
综上所述,p的取值范围是(-∞,1).[例6] 函数f(x)=1+log2x与g(x)=2-x+1在同一直角坐标系下的大致图象是
( )
[答案] C
[解析] f(x)的图象过点(1,1),g(x)的图象过点(0,2),只有C符合,故选C.[例2] 比较a2x2+1与ax2+2(a>0,a≠1)的大小.
[解析] (1)当a>1时,
①若2x2+1>x2+2,即x>1或x<-1,则a2x2+1>ax2+2;
②若2x2+1=x2+2,即x=±1,则a2x2+1=ax2+2;
③若2x2+1①若2x2+1>x2+2,即x>1或x<-1,则a2x2+1②若2x2+1=x2+2,即x=±1,则a2x2+1=ax2+2;
③若2x2+1ax2+2.
[例3] (2010·广东理,3)若函数f(x)=3x+3-x与g(x)=3x-3-x的定义域均为R,则
( )
A.f(x)与g(x)均为偶函数
B.f(x)为偶函数,g(x)为奇函数
C.f(x)与g(x)均为奇函数
D.f(x)为奇函数,g(x)为偶函数
[答案] B
[解析] ∵f(-x)=3-x+3x=f(x),∴f(x)为偶函数,而g(-x)=3-x-3x=-(3x-3-x)=-g(x),∴g(x)为奇函数.
[答案] D
[解析] ∵2x>0,∴2x-1>-1
又2x-1≠0,∴2x-1∈(-1,0)∪(0,+∞),
∴y∈(-∞,-1)∪(0,+∞),故选D.[例5] 设函数f(x)=|log3x|,若f(a)>f(2),求a的取值范围.三、注重数学思想方法的掌握
1.函数与方程的思想.
[例1] 已知关于x的方程2a2x-2-7ax-1+3=0有一个根是2,求a的值和方程其余的根.[分析] 本题给出的的方程有两个变量x、a,要使之有确定的值必须附加一个条件,题中的条件“有一个根为2”正是依据这种需要给出的.因此将x=2代入方程消去x,得到一个关于a的一元二次方程,是解题的基本途径;此外,对于解指数方程,如果习惯于用换元法,令ax-1=y,同样可得到一个关于y的一元二次方程,但须注意,由于表达y的代数式有两个变量,仍需运用条件“x=2”才能确定a的值.同时,因为本题的一元二次方程有两个不同的实数根,故必须由a或y的不同值分别求出x的另一个值.
2.分类讨论的思想
[例2] 设x=loga(a3+1),y=loga(a2+1),a>0,且a≠1,则x,y的大小关系是
( )
A.x>y B.xC.x=y D.与a有关
[解析] ∵(a3+1)-(a2+1)=a2(a-1),
∴a>1时,a3+1>a2+1,从而x>y;
0y,综上可知x>y,
故选A.[点评] 对数函数y=logax的单调性是按a>1与0分类定义的.[例4] 函数y=a2x+2ax-1(a>0且a≠1)在区间[-1,1]上有最大值14,求a的值.3.转化与化归的思想
[例5] 关于x的方程4x-2x+a=0有解,求a的取值范围.
[分析] 设t=2x,则问题可变为讨论一元二次方程t2-t+a=0在区间(0,+∞)上有解的问题,讨论较为繁琐,可以把问题转换成a=-t2+t在(0,+∞)上有解,进一步把问题转换成求函数y=-t2+t在(0,+∞)上的值域.
一、熟练掌握指数幂的定义、运算法则、公式和对数的定义、运算法则、公式是指对函数及其一切运算赖以施行的基础
1.指数幂的定义与运算[答案] D[例2] 方程2x-x2=2x+1的解的个数为______.
[解析] 原方程即2x=x2+2x+1,在同一坐标系中画出y=2x,y=x2+2x+1的图象,由图象可知有3个交点.[例3] 0.32,log20.3,20.3这三数之间的大小顺序是( )
A.0.32<20.3
D.log20.3<20.3<0.32
[分析] 可分别画出y=2x,y=log2x与y=x2的图象用图象来解决,也可以由幂、指、对函数值的分布规律解决.
[解析] 如图,
在同一坐标系中作出函数y=2x,y=x2及y=log2x的图象.
观察图象知当x=0.3时,log20.3<0.32<20.3.选C.[例4] 方程log3x+x=3的解所在的区间是( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,+∞)
[解析] 直接解方程是无法实现的,而借助于数形结合思想作出图象,则问题易于解决.
设y1=log3x,y2=-x+3,在同一坐标系中画出它们的图象(如下图)观察可排除A,D.其交点P的横坐标应在(1,3)内.
又x=2时,y1=log32<1,
而y2=-x+3=1,且知y1是增函数,y2是减函数,所以交点P的横坐标应在(2,3)内,∴选C.[例5] 设x∈(0,1)时,函数y=xp的图象在直线y=x的上方,则p的取值范围是________.
[解析] (1)当p>0时,根据题意p<1,∴0
(3)当p<0时,在(0,+∞)上过(1,1)点,函数为减函数,符合题意.
综上所述,p的取值范围是(-∞,1).[例6] 函数f(x)=1+log2x与g(x)=2-x+1在同一直角坐标系下的大致图象是
( )
[答案] C
[解析] f(x)的图象过点(1,1),g(x)的图象过点(0,2),只有C符合,故选C.[例2] 比较a2x2+1与ax2+2(a>0,a≠1)的大小.
[解析] (1)当a>1时,
①若2x2+1>x2+2,即x>1或x<-1,则a2x2+1>ax2+2;
②若2x2+1=x2+2,即x=±1,则a2x2+1=ax2+2;
③若2x2+1
③若2x2+1
[例3] (2010·广东理,3)若函数f(x)=3x+3-x与g(x)=3x-3-x的定义域均为R,则
( )
A.f(x)与g(x)均为偶函数
B.f(x)为偶函数,g(x)为奇函数
C.f(x)与g(x)均为奇函数
D.f(x)为奇函数,g(x)为偶函数
[答案] B
[解析] ∵f(-x)=3-x+3x=f(x),∴f(x)为偶函数,而g(-x)=3-x-3x=-(3x-3-x)=-g(x),∴g(x)为奇函数.
[答案] D
[解析] ∵2x>0,∴2x-1>-1
又2x-1≠0,∴2x-1∈(-1,0)∪(0,+∞),
∴y∈(-∞,-1)∪(0,+∞),故选D.[例5] 设函数f(x)=|log3x|,若f(a)>f(2),求a的取值范围.三、注重数学思想方法的掌握
1.函数与方程的思想.
[例1] 已知关于x的方程2a2x-2-7ax-1+3=0有一个根是2,求a的值和方程其余的根.[分析] 本题给出的的方程有两个变量x、a,要使之有确定的值必须附加一个条件,题中的条件“有一个根为2”正是依据这种需要给出的.因此将x=2代入方程消去x,得到一个关于a的一元二次方程,是解题的基本途径;此外,对于解指数方程,如果习惯于用换元法,令ax-1=y,同样可得到一个关于y的一元二次方程,但须注意,由于表达y的代数式有两个变量,仍需运用条件“x=2”才能确定a的值.同时,因为本题的一元二次方程有两个不同的实数根,故必须由a或y的不同值分别求出x的另一个值.
2.分类讨论的思想
[例2] 设x=loga(a3+1),y=loga(a2+1),a>0,且a≠1,则x,y的大小关系是
( )
A.x>y B.x
[解析] ∵(a3+1)-(a2+1)=a2(a-1),
∴a>1时,a3+1>a2+1,从而x>y;
0
故选A.[点评] 对数函数y=logax的单调性是按a>1与0
[例5] 关于x的方程4x-2x+a=0有解,求a的取值范围.
[分析] 设t=2x,则问题可变为讨论一元二次方程t2-t+a=0在区间(0,+∞)上有解的问题,讨论较为繁琐,可以把问题转换成a=-t2+t在(0,+∞)上有解,进一步把问题转换成求函数y=-t2+t在(0,+∞)上的值域.
