高中数学人教新课标必修1:第二章 基本初等函数(ⅰ) 指数函数及其性质
文档属性
| 名称 | 高中数学人教新课标必修1:第二章 基本初等函数(ⅰ) 指数函数及其性质 |

|
|
| 格式 | rar | ||
| 文件大小 | 878.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-01-06 00:00:00 | ||
图片预览








文档简介
课件47张PPT。2.1.2 指数函数及其性质
阅读教材P54~57,回答下列问题:
1.函数 叫做指数函数,指数函数的定义域是 ,值域为 .
2.指数函数的图象,当 时,象“一撇”, 时,象“一捺”.
3.指数函数的图象特征
(1)这些图象都位于x轴的 ;
(2)这些图象都经过 点;y=ax(a>0,a≠1)(0,+∞)Ra>101)的图象在第一象限内的纵坐标都大于1,在第二象限的纵坐标都小于1且大于0;y=ax(0就是说,当a>1,x>0时,y∈ .
当a>1,x<0时,y∈ .
当00时,y∈ .
当0指出下列哪些数大于1,哪些数小于1?(1,+∞)(0,1)(0,1)(1,+∞)
(4)从左往右看,y=ax(a>1)的图象逐渐上升;y=ax(0这就是说,当 时,y=ax为增函数,当 时,y=ax为减函数.
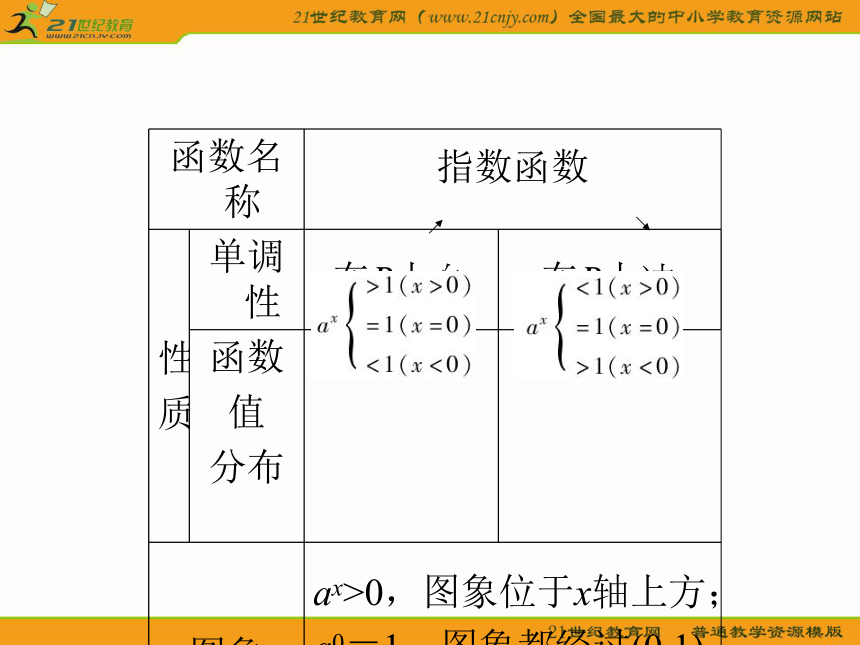
若y=(2a-1)x为增函数,则a的取值范围是 .a>1014.将指数函数的图象和性质总结如下表(-1,1) (0,+∞) [0,+∞) R (5)比较大小,用“<”或“>”连接下列每组中的两个数.
本节重点:指数函数的图象与性质.
本节难点:函数值的变化规律.
[例1] 下列函数中,哪些是指数函数?
(1)y=4x;
(2)y=x4;
(3)y=-4x;
(4)y=(-4)x;
(5)y=πx;
(6)y=4x2;
(7)y=xx;
[解析] (1)、(5)、(8)为指数函数;
(2)中底数x不是常数,而4不是变数;
(3)是-1与指数函数4x的乘积;
(4)中底数-4<0,∴不是指数函数;
(6)中指数不是自变量x,而是x的函数;
(7)中底数x不是常数.
它们都不符合指数函数的定义.[例2] 指数函数y=f(x)的图象经过点(π,e),求f(0),f(1),f(-π)的值.
[解析] 设y=f(x)=ax,
∵它的图象经过点(π,e), 总结评述:已知函数类型,用待定系数法求函数解析式是常用 的一般方法.[答案] f(-2)[例3] 比较下列每组中两个数的大小:
①1.72.5,1.73
②0.8-0.1,0.8-0.2
③1.70.3,0.93.1
[分析] 分析各数的构成特征,将其看作指数函数的两个函数值,用单调性得出结论,或直接运用指数函数值的分布规律求解.[解析] ①考察指数函数y=1.7x,由于底数1.7>1,所以指数函数y=1.7x在(-∞,+∞)上是增函数.
∵2.5<3,∴1.72.5<1.73.
②考察函数y=0.8x,由于0<0.8<1,
所以指数函数y=0.8x在(-∞,+∞)上为减函数.
∵-0.1>-0.2,∴0.8-0.1<0.8-0.2.
③由指数函数的性质得
1.70.3>1.70=1, 0.93.1<0.90=1,
∴1.70.3>0.93.1.[例5] 如图是指数函数①y=ax;②y=bx;③y=cx;④y=dx的图象,则a、b、c、d与1的大小关系是( )A.aC.1[分析] 比较a、b、c、d的大小,即比较x=1时各函数值的大小,即对应点的高低.
[解析] 解法1:在①②中底数小于1且大于零,在y轴右边,底数越小,图象越靠近x轴,故有b解法2:设x=1与①、②、③、④的图象分别交于点A,B,C,D,则其坐标依次为(1,a),(1,b),(1,c),(1,d),由图象观察可得c>d>1>a>b.故选B.
[点评] 总结规律如下:
当指数函数底数大于1时,图象上升,且当底数越大,图象向上越靠近于y轴,当底数大于0小于1时,图象下降,底数越小,图象向下越靠近于x轴.简称x>0时,底大图高.[答案] C
[解析] 解法一:指数函数y=ax的图象从第一象限看,逆时针方向底数a依次从小变大,故选C.[例6] 求下列函数的定义域和值域:
[分析] 结合指数函数的定义域和值域考虑.
[解析] (1)令x-4≠0得x≠4
∴定义域为{x|x∈R且x≠4}(3)定义域为R
∵y=4x+2x+1+1=(2x)2+2·2x+1
=(2x+1)2且2x>0,∴y>1
故y=4x+2x+1+1的值域为{y|y>1}.
分别写出下列函数的定义域和值域:[解析] (1)R,{y|y>0}.
(2){x|x≤0},{y|0≤y<1}.
(3){x|x≥0},{y|y≥1}.
(4)x∈R,{y|y≥1}.
(5){x|x≥1},{y|y≥0}.[例7] 已知方程9x-2·3x+3k-1=0有两个实数解,试求实数k的取值范围.[辨析] 换元后t=3x>0,原方程有两个实数解,则关于“新元”t的方程※应有两个正数解,而Δ≥0,只能保证方程※有两个实数解,不能保证原方程有两个实数解.事实上,当方程※有两个负根时,原方程无解.一、选择题
1.函数f(x)=3-x-1的定义域、值域是 ( )
A.定义域是R,值域是R
B.定义域是R,值域是(0,+∞)
C.定义域是R,值域是(-1,+∞)
D.以上都不对
[答案] C
[解析] 由y=3-x-1知定义域x∈R,
∵3-x>0,∴3-x-1>-1,
∴值域为y∈(-1,+∞).故选C.2.函数y=(p2-1)x在(-∞,+∞)上是增函数,则实数p的取值范围是 ( )
[答案] C3.下列函数中值域为(0,+∞)的是 ( )
[答案] D
[解析] 选项A值域为(0,1)∪(1,+∞);选项B值域为[0,1);选项C值域为[0,+∞),故选D.
二、填空题
4.无论a取何值(a>0且a≠1),函数y=2+ax+3的图象恒过定点________.
[答案] (-3,3)
[解析] 由指函数y=ax(a>0且a≠1)过定点(0,1)知,x+3=0时,ax+3=1.
∴此函数图象过定点(-3,3).5.比较大小,填“>”,“<”
①2.32.5______2.33.2; ②0.4-1.5______0.4-1.3;
[答案] <,>,>,<
[解析] ①∵y=2.3x为增函数,2.5<3.2,
∴2.32.5<2.33.2;
②∵y=0.4x为减函数,-1.5<-1.3,
∴0.4-1.5>0.4-1.3;
阅读教材P54~57,回答下列问题:
1.函数 叫做指数函数,指数函数的定义域是 ,值域为 .
2.指数函数的图象,当 时,象“一撇”, 时,象“一捺”.
3.指数函数的图象特征
(1)这些图象都位于x轴的 ;
(2)这些图象都经过 点;y=ax(a>0,a≠1)(0,+∞)Ra>10
当a>1,x<0时,y∈ .
当0
当0
(4)从左往右看,y=ax(a>1)的图象逐渐上升;y=ax(0
若y=(2a-1)x为增函数,则a的取值范围是 .a>10
本节重点:指数函数的图象与性质.
本节难点:函数值的变化规律.
[例1] 下列函数中,哪些是指数函数?
(1)y=4x;
(2)y=x4;
(3)y=-4x;
(4)y=(-4)x;
(5)y=πx;
(6)y=4x2;
(7)y=xx;
[解析] (1)、(5)、(8)为指数函数;
(2)中底数x不是常数,而4不是变数;
(3)是-1与指数函数4x的乘积;
(4)中底数-4<0,∴不是指数函数;
(6)中指数不是自变量x,而是x的函数;
(7)中底数x不是常数.
它们都不符合指数函数的定义.[例2] 指数函数y=f(x)的图象经过点(π,e),求f(0),f(1),f(-π)的值.
[解析] 设y=f(x)=ax,
∵它的图象经过点(π,e), 总结评述:已知函数类型,用待定系数法求函数解析式是常用 的一般方法.[答案] f(-2)
①1.72.5,1.73
②0.8-0.1,0.8-0.2
③1.70.3,0.93.1
[分析] 分析各数的构成特征,将其看作指数函数的两个函数值,用单调性得出结论,或直接运用指数函数值的分布规律求解.[解析] ①考察指数函数y=1.7x,由于底数1.7>1,所以指数函数y=1.7x在(-∞,+∞)上是增函数.
∵2.5<3,∴1.72.5<1.73.
②考察函数y=0.8x,由于0<0.8<1,
所以指数函数y=0.8x在(-∞,+∞)上为减函数.
∵-0.1>-0.2,∴0.8-0.1<0.8-0.2.
③由指数函数的性质得
1.70.3>1.70=1, 0.93.1<0.90=1,
∴1.70.3>0.93.1.[例5] 如图是指数函数①y=ax;②y=bx;③y=cx;④y=dx的图象,则a、b、c、d与1的大小关系是( )A.a
[解析] 解法1:在①②中底数小于1且大于零,在y轴右边,底数越小,图象越靠近x轴,故有b
[点评] 总结规律如下:
当指数函数底数大于1时,图象上升,且当底数越大,图象向上越靠近于y轴,当底数大于0小于1时,图象下降,底数越小,图象向下越靠近于x轴.简称x>0时,底大图高.[答案] C
[解析] 解法一:指数函数y=ax的图象从第一象限看,逆时针方向底数a依次从小变大,故选C.[例6] 求下列函数的定义域和值域:
[分析] 结合指数函数的定义域和值域考虑.
[解析] (1)令x-4≠0得x≠4
∴定义域为{x|x∈R且x≠4}(3)定义域为R
∵y=4x+2x+1+1=(2x)2+2·2x+1
=(2x+1)2且2x>0,∴y>1
故y=4x+2x+1+1的值域为{y|y>1}.
分别写出下列函数的定义域和值域:[解析] (1)R,{y|y>0}.
(2){x|x≤0},{y|0≤y<1}.
(3){x|x≥0},{y|y≥1}.
(4)x∈R,{y|y≥1}.
(5){x|x≥1},{y|y≥0}.[例7] 已知方程9x-2·3x+3k-1=0有两个实数解,试求实数k的取值范围.[辨析] 换元后t=3x>0,原方程有两个实数解,则关于“新元”t的方程※应有两个正数解,而Δ≥0,只能保证方程※有两个实数解,不能保证原方程有两个实数解.事实上,当方程※有两个负根时,原方程无解.一、选择题
1.函数f(x)=3-x-1的定义域、值域是 ( )
A.定义域是R,值域是R
B.定义域是R,值域是(0,+∞)
C.定义域是R,值域是(-1,+∞)
D.以上都不对
[答案] C
[解析] 由y=3-x-1知定义域x∈R,
∵3-x>0,∴3-x-1>-1,
∴值域为y∈(-1,+∞).故选C.2.函数y=(p2-1)x在(-∞,+∞)上是增函数,则实数p的取值范围是 ( )
[答案] C3.下列函数中值域为(0,+∞)的是 ( )
[答案] D
[解析] 选项A值域为(0,1)∪(1,+∞);选项B值域为[0,1);选项C值域为[0,+∞),故选D.
二、填空题
4.无论a取何值(a>0且a≠1),函数y=2+ax+3的图象恒过定点________.
[答案] (-3,3)
[解析] 由指函数y=ax(a>0且a≠1)过定点(0,1)知,x+3=0时,ax+3=1.
∴此函数图象过定点(-3,3).5.比较大小,填“>”,“<”
①2.32.5______2.33.2; ②0.4-1.5______0.4-1.3;
[答案] <,>,>,<
[解析] ①∵y=2.3x为增函数,2.5<3.2,
∴2.32.5<2.33.2;
②∵y=0.4x为减函数,-1.5<-1.3,
∴0.4-1.5>0.4-1.3;
