随机事件的概率（公开课）

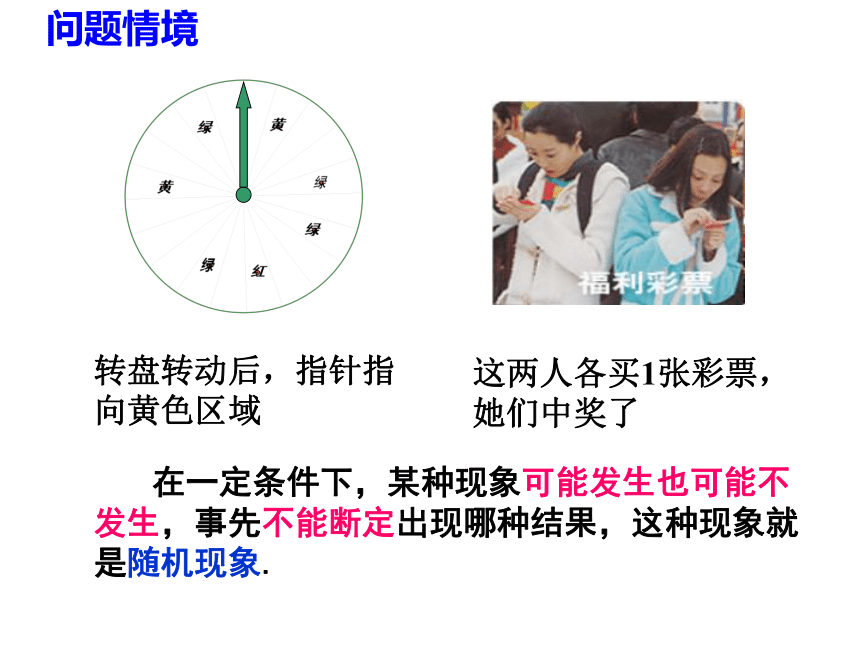
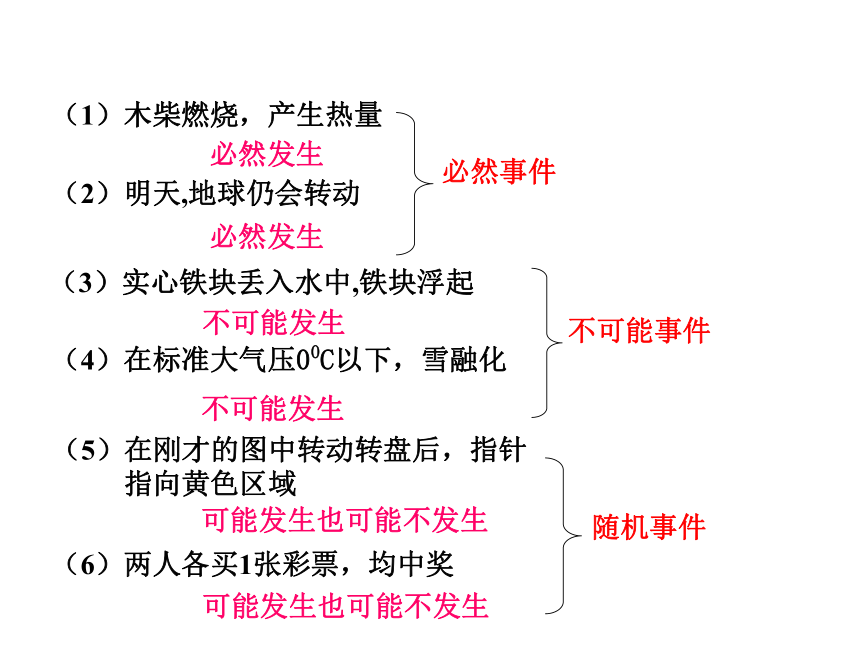
课件21张PPT。随机事件的概率 在一定条件下，某种现象可能发生也可能不发生，事先不能断定出现哪种结果，这种现象就是随机现象.这两人各买1张彩票，她们中奖了问题情境明天，地球还会转动在00C下，这些雪融化 在一定条件下，事先就能断定发生或不发生某种结果，这种现象就是确定性现象.实心铁块丢入水中,铁块浮出水面（1）木柴燃烧，产生热量（2）明天,地球仍会转动
（3）实心铁块丢入水中,铁块浮起（4）在标准大气压00C以下，雪融化（5）在刚才的图中转动转盘后，指针
指向黄色区域（6）两人各买1张彩票，均中奖不可能发生必然发生必然发生不可能发生可能发生也可能不发生可能发生也可能不发生随机事件：在一定条件下可能发生也可能不发生的事
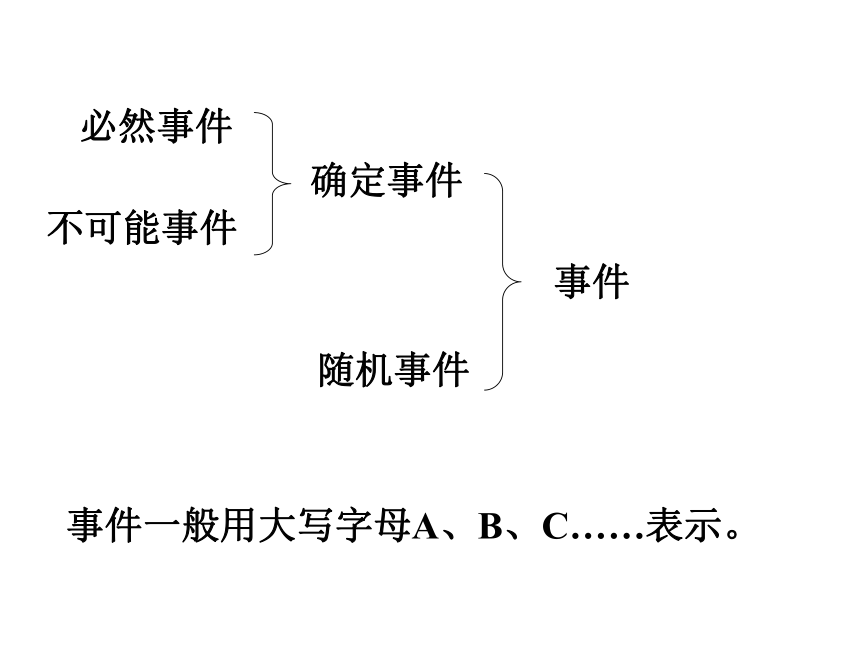
件叫随机事件。必然事件：在一定条件下必然要发生的事件叫必然事件。不可能事件：在一定条件下不可能发生的事件叫不可
能事件。数学理论必然事件不可能事件随机事件事件一般用大写字母A、B、C……表示。随机事件的概率让我们来做一个试验：注：
投10次硬币、并记录正面向上的次数，算出正面向上的比例，填好表格。1. 频率的定义 投掷一枚硬币，出现正面可能性有多大？ 历史上也曾有人做过抛掷硬币的大量重复试验，结果如下表 ：抛硬币试验结论：当试验次数很大时，硬币正面向上的频率接近于常数0.5，并在其附近摆动.2. 概率的定义 在大量重复进行同一试验时，事件 A 发生
的频率 总是接近于某个常数，在它附近摆
动，这时就把这个常数叫做事件A 的概率．记作： P(A)。两点注意：1.随机事件A的概率范围必然事件的概率为1，不可能事件的概率是0。即0≤P(A)≤1 ， 随机事件的概率是0(4)随着试验次数的增加，频率越来越接近概率。(3)概率是频率的稳定值，频率是概率的近似值。
(5)概率反映了随机事件发生的可能性的大小。
2.频率与概率的区别与联系：练一练BC3.某篮球运动员在同一条件下进行投篮练习,结果如下表:计算表中进球的频率;
这位运动员投篮一次,进球的概率约是多少?(3)这位运动员进球的概率是0.8,那么他投10次篮一定能
投中8次吗?不一定. 投10次篮相当于做10次试验,每次试验的结果都是随机的, 所以投10次篮的结果也是随机的. 但随着投篮次数的增加,他进球的可能性为80%.概率约是0.80.800.750.800.80 0.85 0.830.75总结：1、了解必然事件、不可能事件、随机事件2、理解随机事件的概率的定义3、掌握概率的范围：0≤P(A)≤14、明确频率与概率的区别与联系。 在第二次世界大战中，美国曾经宣布：一名优秀数学家的作用超过10个师的兵力．这句话有一个非同寻常的来历．
1943年以前，在大西洋上英美运输船队常常受到德国潜艇的袭击，当时，英美两国限于实力，无力增派更多的护航舰，一时间，德军的“潜艇战”搞得盟军焦头烂额．
为此，有位美国海军将领专门去请教了几位数学家，数学家们运用概率论分析后，舰队与敌潜艇相遇是一个随机事件，从数学角度来看这一问题，它具有一定的规律性．一定数量的船（为100艘）编队规模越小，编次就越多（为每次20艘，就要有5个编次），编次越多，与敌人相遇的概率就越大．
美国海军接受了数学家的建议，命令舰队在指定海域集合，再集体通过危险海域，然后各自驶向预定港口．结果奇迹出现了：盟军舰队遭袭被击沉的概率由原来的25％降为1％，大大减少了损失，保证了物资的及时供应．1名数学家＝10个师这个故事告诉我们数学知识在实际生活中的作用是巨大的，特别是当今社会，随着信息时代的到来， 知识正改变着未来，改变着世界,改变着着我们周围的一切。让我们一起努力吧！作业布置《学海导航》随机事件的概率
（第一课时）学习愉快再见！