3.1.1 数系的扩充与复数的概念
文档属性
| 名称 | 3.1.1 数系的扩充与复数的概念 |
|
|
| 格式 | rar | ||
| 文件大小 | 160.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-01-11 00:00:00 | ||
图片预览






文档简介
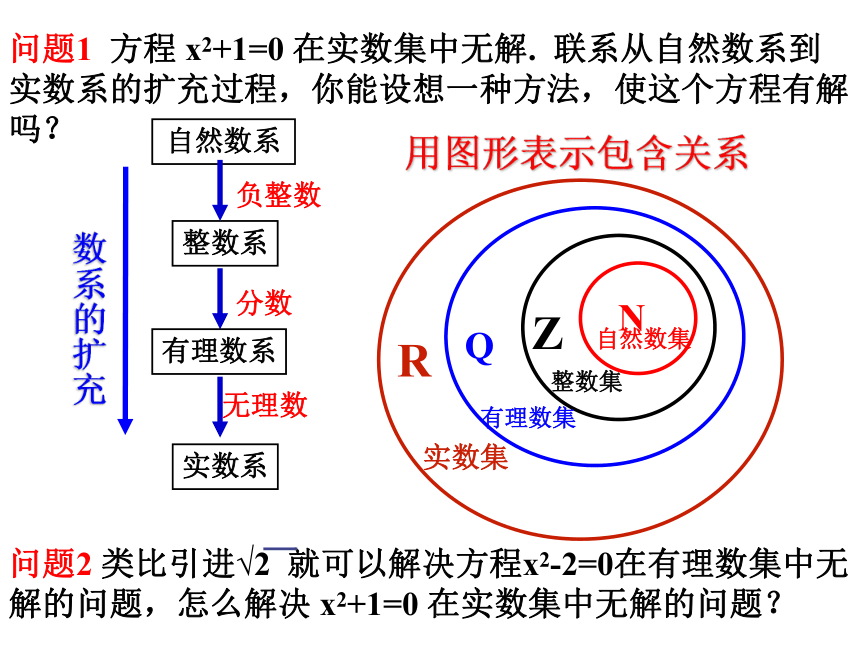
课件13张PPT。用图形表示包含关系问题1 方程 x2+1=0 在实数集中无解. 联系从自然数系到实数系的扩充过程,你能设想一种方法,使这个方程有解吗?引入一个新数:使 i 是方程 x2+1=0 的根,即使 i 2 = -1 .问题3 把实数和新引入的数 i 像实数那样进行加法、乘法运算,并希望运算时有关的运算律仍成立,你得到了什么样的数?3.1.1 数系的扩充与复数的概念 现在我们就引入这样一个数 i ,把 i 叫做虚数单位,并且规定:
(1)i2 ??1 ;
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算律(包括交换律、结合律和分配律)仍然成立。形如 a+bi (a,b∈R) 的数叫做复数. 全体复数所形成的集合叫做复数集,
一般用字母C表示 .即C={ a+bi | a,b∈R}复数的代数形式:通常用字母 z 表示,即其中 称为虚数单位。问题4 你认为应该怎样定义两个复数相等? 如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.例1 已知 ,其中 求解:根据复数相等的定义,得方程组解得特别地,复数z=a+bi问题6 复数集C和实数集R之间有什么关系?问题5 复数 a + bi 在什么条件下是实数?复数集
C实数集
R虚数集纯虚数集实数虚数纯虚数(b = 0)(b≠0)(a=0,且b≠0)你知道吗?一般来说,两个复数的关系只能说相等或不相等,因为虚数不能比较大小,只有两个实数才可以比较大小.5i -2 02、判断下列命题是否正确:
(1)若a、b为实数,则z=a+bi 为虚数;
(2)若b为实数,则z=bi 必为纯虚数;
(3)若a为实数,则z=a 一定不是虚数.练一练:1、说出下列复数中哪些是实数,哪些是虚数,哪些是纯虚数?√××例2 实数m取什么值时,复数
是(1)实数? (2)虚数? (3)纯虚数?解: (1)当 m-1=0 ,(2)当 ,即 时,复数z 是虚数.(3)当即 时,复数z 是
纯虚数.实部 即m=1时,复数z 是实数.虚部练一练:当m为何实数时,复数
是 (1)实数? (2)虚数? (3)纯虚数?2、已知集合M={1 , (t2-2t)+(t2+t-2)i },p={ -1, 1, 4i} ,若M∪P=P,求实数t的值.小结:1.虚数单位i的引入;作业
见课本P106 :
习题3.1中A组 1 , 2 , 3
(1)i2 ??1 ;
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算律(包括交换律、结合律和分配律)仍然成立。形如 a+bi (a,b∈R) 的数叫做复数. 全体复数所形成的集合叫做复数集,
一般用字母C表示 .即C={ a+bi | a,b∈R}复数的代数形式:通常用字母 z 表示,即其中 称为虚数单位。问题4 你认为应该怎样定义两个复数相等? 如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.例1 已知 ,其中 求解:根据复数相等的定义,得方程组解得特别地,复数z=a+bi问题6 复数集C和实数集R之间有什么关系?问题5 复数 a + bi 在什么条件下是实数?复数集
C实数集
R虚数集纯虚数集实数虚数纯虚数(b = 0)(b≠0)(a=0,且b≠0)你知道吗?一般来说,两个复数的关系只能说相等或不相等,因为虚数不能比较大小,只有两个实数才可以比较大小.5i -2 02、判断下列命题是否正确:
(1)若a、b为实数,则z=a+bi 为虚数;
(2)若b为实数,则z=bi 必为纯虚数;
(3)若a为实数,则z=a 一定不是虚数.练一练:1、说出下列复数中哪些是实数,哪些是虚数,哪些是纯虚数?√××例2 实数m取什么值时,复数
是(1)实数? (2)虚数? (3)纯虚数?解: (1)当 m-1=0 ,(2)当 ,即 时,复数z 是虚数.(3)当即 时,复数z 是
纯虚数.实部 即m=1时,复数z 是实数.虚部练一练:当m为何实数时,复数
是 (1)实数? (2)虚数? (3)纯虚数?2、已知集合M={1 , (t2-2t)+(t2+t-2)i },p={ -1, 1, 4i} ,若M∪P=P,求实数t的值.小结:1.虚数单位i的引入;作业
见课本P106 :
习题3.1中A组 1 , 2 , 3
