3.1.2 复数的几何意义

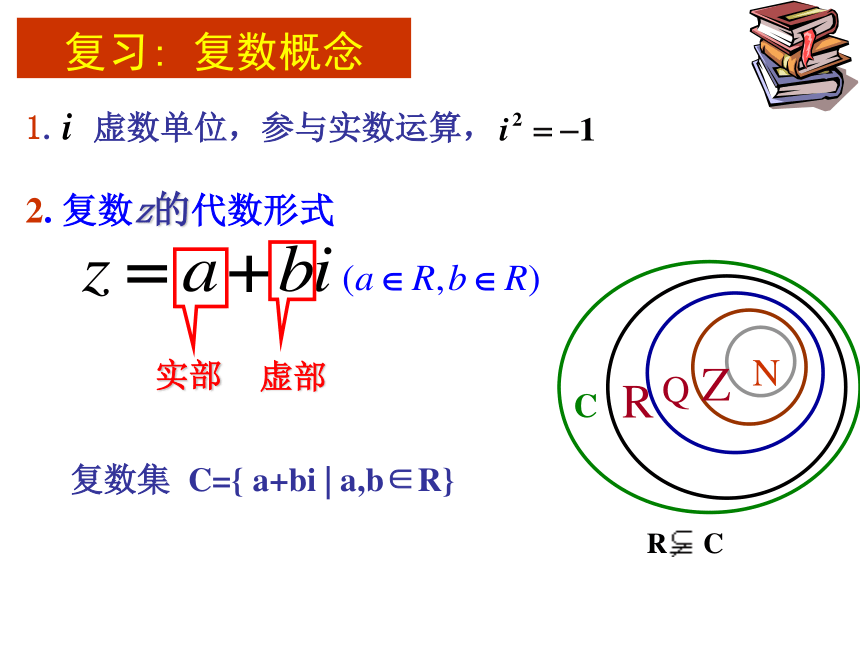
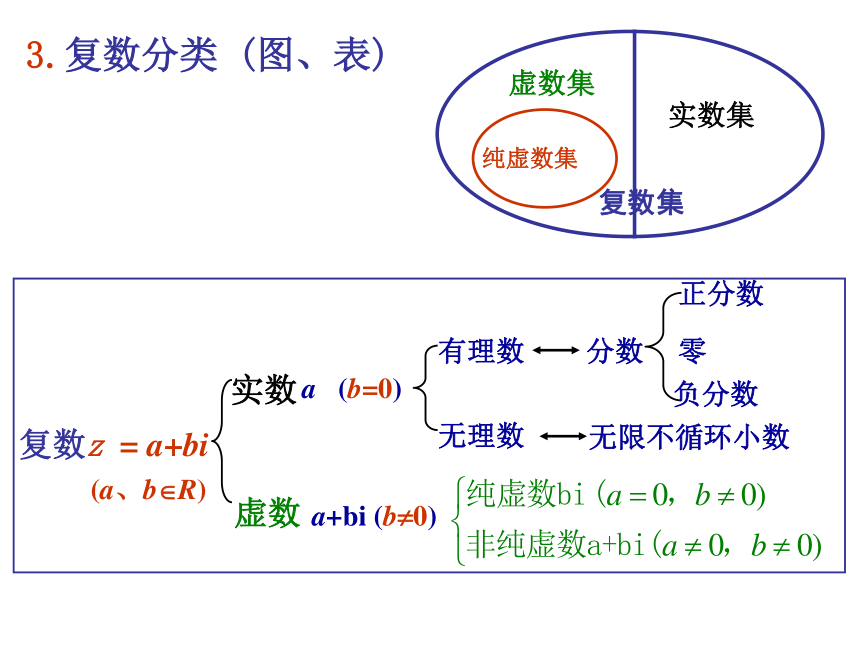
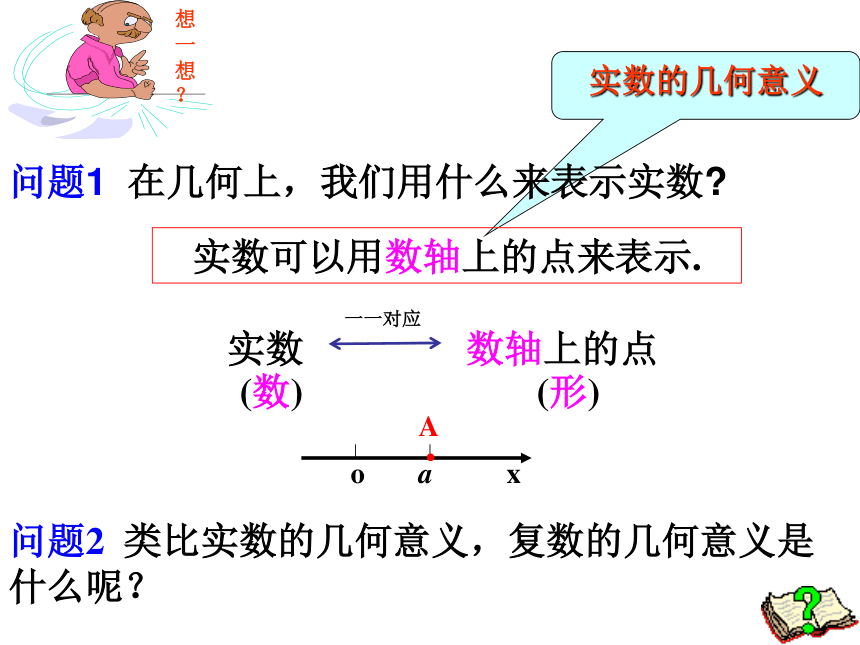
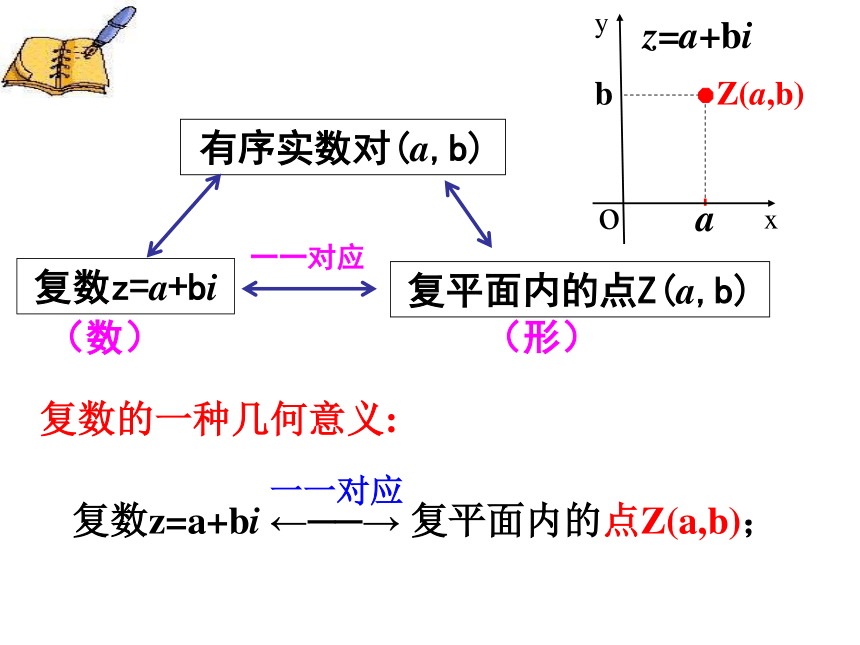
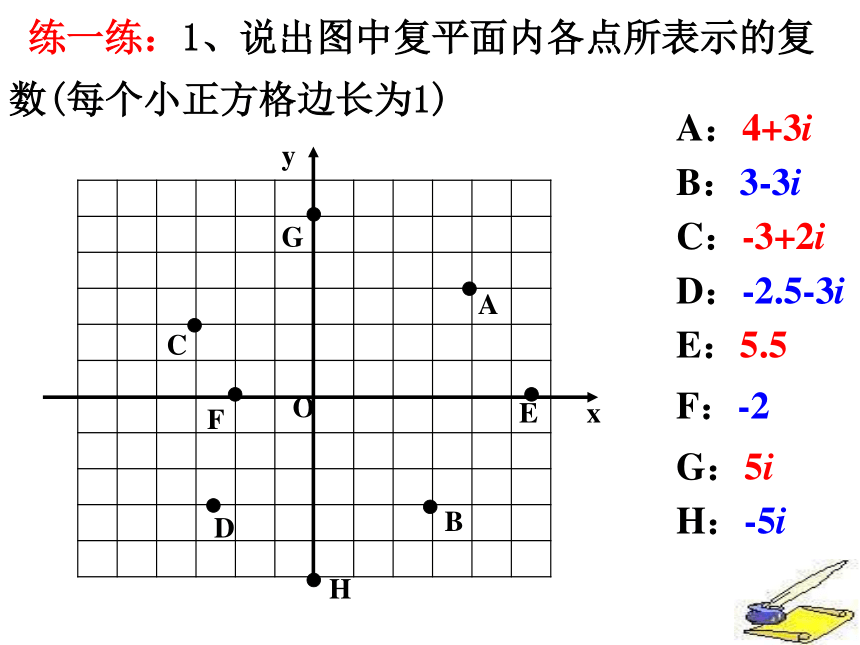
课件18张PPT。3.1.2 复数的几何意义1. 虚数单位，参与实数运算，复习: 复数概念3.复数分类 (图、表)实数的几何意义实数可以用数轴上的点来表示.问题2 类比实数的几何意义，复数的几何意义是什么呢？问题1 在几何上，我们用什么来表示实数?想一想？ 根据复数相等的定义，每一个复数z=a+bi，都可以用一个有序实数对(a,b)唯一确定. 由于有序实数对(a,b)与平面直角坐标系中的点一一对应，因此复数集与平面直角坐标系中的点集之间可以建立一一对应.定义：建立了平面直角坐标系来表示复数的平面叫做复平面.x轴---实轴y轴---虚轴虚轴实轴问题2 类比实数的几何意义，复数的几何意义是什么呢？实轴上的点都表示实数除了原点外，虚轴上的点都表示纯虚数复数的一种几何意义: 复数z=a+bi ←──→ 复平面内的点Z(a,b)；一一对应 练一练：1、说出图中复平面内各点所表示的复数(每个小正方格边长为1)OxyAEBHDFCGA：4+3iB：3-3iC：-3+2iD：-2.5-3iE：5.5F：-2G：5iH：-5i2、说出每个复数在复平面内所对应的点的坐标. 2 + 5i ;
(2) -3 + 2i ;
(3) 2 - 4i ;
(4) -3 - i ;
(5) 5 ;
(6) -3i . (2 , 5) ; (2) (-3 , 2) ; (3) (2 , – 4) ; (4) (-3 , -1 ) ; (5) (5 , 0) ; (6) (0 , -3) .(A)在复平面内，对应于实数的点都在实轴上；
(B)在复平面内，对应于纯虚数的点都在虚轴上；
(C)在复平面内，实轴上的点所对应的复数都是实数；
(D)在复平面内，虚轴上的点所对应的复数都是纯虚数.3、下列命题中的假命题是（ ）D例1 已知复数z=(m-6)+(m-1)i在复平面内所对应的点位于第二象限，求实数m的取值范围。 一种重要的数学思想：数形结合思想变式 已知复数z=(m-6)+(m-1)i在复平面内所对应的点在直线x-2y+3=0上，求实数m的值。 解：∵复数z=(m-6)+(m-1)i在复平面内所对应的点是（m-6，m-1）， ∴(m-6)-2(m-1)+3=0 ， ∴ m=-1. 例1 已知复数z=(m-6)+(m-1)i在复平面内所对应的点位于第二象限，求实数m的取值范围。 复数z=a+bi复平面内的点Z(a,b)一一对应平面向量一一对应一一对应 在平面直角坐标系中，每一个平面向量都可以用一个有序实数对来表示，而有序实数对与复数是一一对应的.复数的第二种几何意义:BC2 - 3i- 2 - 3i复数的模|z| =|a+bi|=rr记作： | z | 或 | a+bi |一个重要结论： 例3 求下列复数的模：
(1) z1 = -5i
(2) z2 = -3+4i
(3) z3 = 5-5i(4) z4 = 1+mi(m∈R)
(5) z5 = 4a-3ai(a<0)|z| =|a+bi|=r例4思考题：(1)满足|z|=5(z∈R)的z值有几个？ (3)满足|z|=5(z∈C)的复数z对应的点在复平面上构成怎样的图形？ (2)满足|z|=5(z∈C)的z值有几个？±5设z=x+yi(x,y∈R)图形:以原点为圆心,5为半径的圆上小 结(1) 复数z=a+bi ←──→ 复平面内的点Z(a,b)；1、复数的几何意义 (两种)2、复数的模一一对应一一对应作业：
见课本P106中习题3.1
A组 5 , 6 B组 2 ，3