古典概型
图片预览








文档简介
课件21张PPT。古典概型一.复习:随机事件及其概率1.在一定的条件下必然要发生的事件;叫必然事件;2.在一定的条件下不可能发生的事件;叫不可能事件;3.在一定的条件下可能发生也可能不发生的事件;叫随机事件.4.随机事件的概率5.随机事件的概率性质 1) 0≤P(A)≤1,不可能事件的概率为0,必然事件的概率为1. 2) 如果事件A与事件B互斥,则 P(A∪B)=P(A)+P(B)3)如果事件A与事件B是对立事件时,有 P(A)=1- P(B)互斥事件与对立事件的区别与联系:
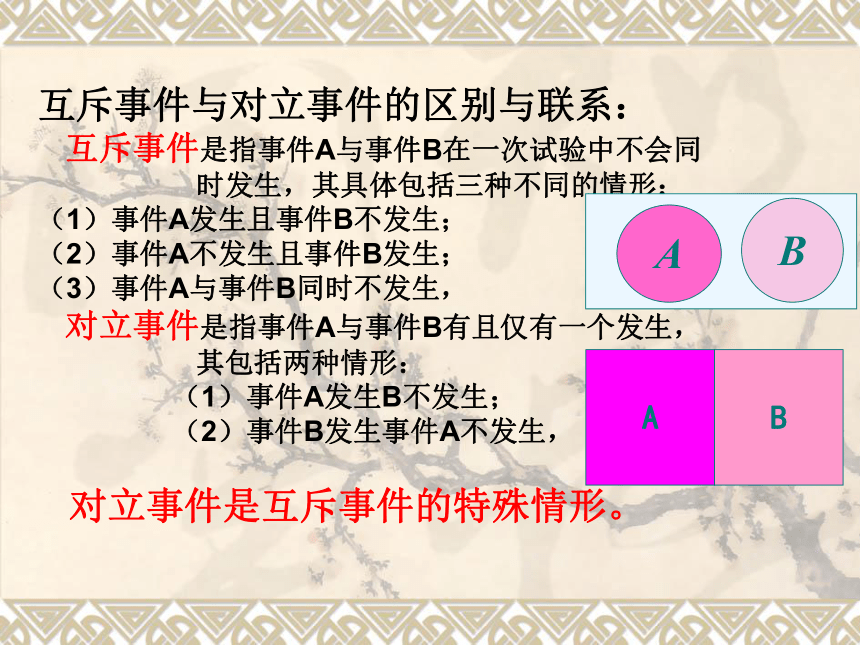
互斥事件是指事件A与事件B在一次试验中不会同
时发生,其具体包括三种不同的情形:
(1)事件A发生且事件B不发生;
(2)事件A不发生且事件B发生;
(3)事件A与事件B同时不发生,
对立事件是指事件A与事件B有且仅有一个发生,
其包括两种情形:
(1)事件A发生B不发生;
(2)事件B发生事件A不发生,
对立事件是互斥事件的特殊情形。
AB对于随机事件,我们是否只
能通过大量重复试验才能求
其概率呢?有的情况下的大量重复的试验是否可以避免?问题1:抛一枚均匀的硬币,可能出现的结果有:由于硬币是均匀的,可以认为出现这2种结果的可能性是,.这与大量重复试验的结果是一致的. 出现“反面向上”的概率也是正面向上反面向上相等的即可以认为出现“正面向上”的概率是
问题2:抛掷一个骰子,它落地时向上的数可能是……也就是说,出现每一种结果的概率都是这种分析也与大量重复试验的结果是一致的. 即可能出现的结果有6种,且每种结果出现的机会是可能是情形1,2,3,4,5,6之一.
均等的(因为骰子是均匀的)问:什么样的事件的概率可以不通过重复试验,而通过对一次试验中可能出现的结果的分析来计算其概率呢?(1)所有结果出现的可能性都相等(2)所出现的结果是有限的⑴基本事件:一次试验中可能出现的每一个基本结果.如抛掷硬币的试验中,由2个基本事件组成。抛掷一个均
匀的骰子的试验中,由6个基本事件组成。 如果一次试验由n个基本事件组成,而且所有的基本事件
出现 的可能性都相等,那么每一个基本事件的概率都是 1/n 。事件A:试验中的一个事件,它由一个或几个基本事件构成。(2)等可能事件:通过以上两个例子进行归纳: 我们将满足(1)(2)两个条件的随机试验的概率模型成为古典概型。
由于以上这些都是历史上最早研究的概率模型,
对上述的数学模型我们称为古典概型 。(1)所有的基本事件只有有限个。(2)每个基本事件的发生都是等可能的。 (1)向一个圆面内随机地投射一个点,如果该点落在圆内任意一点都是等可能的,你认为这是古典概型吗?为什么? (2)如图,某同学随机地向一靶心进行射击,这一试验的结果只有有限个:命中10环、命中9环……命中5环和不中环。你认为这是古典概型吗?为什么? 因为试验的所有可能结果是圆面内所有的点,试验的所有可能结果数是无限的,虽然每一个试验结果出现的“可能性相同”,但这个试验不满足古典概型的第一个条件。 不是古典概型,因为试验的所有可能结果只有7个,而命中10环、命中9环……命中5环和不中环的出现不是等可能的,即不满足古典概型的第二个条件。 问题:抛掷一个骰子,求骰子落地时向上的数是三的倍数的概率是多少呢? 如果某个事件A包含了其中m个等可能基本事件,那么事件A的概率古典概型的概率应用:掷一颗质地均匀的骰子,观察掷出的点数,
(1)写出所有的基本事件,说明其是否是古典概型。 解:有6个基本事件,分别是“出现1点”,“出现2点”,……,“出现6点”。因为骰子的质地均匀,所以每个基本事件的发生是等可能的,因此它是古典概型。(2)观察掷出的点数,求掷得奇数点的概率。 解:这个试验的基本事件共有6个,即(出现1点)、(出现2点)……、(出现6点)
所以基本事件数n=6,
事件A=(掷得奇数点)=(出现1点,出现3点,出现5点),
其包含的基本事件数m=3 所以,P(A)=0.5(1,2)(1,3)(1,4)(1,5)
(2,3)(2,4)(2,5)
(3,4)(3,5)
(4,5)
因此,共有10个基本事件
(2)记摸到2只白球的事件为事件A,
即(1,2)(1,3)(2,3)故P(A)= 3/10 例1 一只口袋内装有大小相同的5只球,其中3只白球,2只红球,从中一次摸出两只球(1)共有多少基本事件(2)摸出的两只球都是白球的概率是多少?解:(1)分别记白球1,2,3号,红球为4,5号,从中摸出2只球,有如下基本事件(摸到1,2号球用(1,2)表示):(3) 该事件可用Venn图表示在集合I中共有10个元素
在集合A中有3个元素
故P(A)= 3/10变式(3)所取的2个球中都是红球的概率是 ?
(4)取出的两个球一白一红的概率是?解:(3)则基本事件仍为10个,其中两个球都是红球的事件包括1个基本事件,所以,所求事件的概率为解:(4)则基本事件仍为10个,其中取出的两个球一白一红的的事件包括6个基本事件,所以,所求事件的概率为求古典概型的步骤:(1)判断是否为等可能性事件;
(2)计算所有基本事件的总结果数n.
(3)计算事件A所包含的结果数m.
(4)计算 概 率 初 步变式?1、从1,2, 3,4, 5五个数字中,任取两数,求两数都是奇数的概率。解:试验的样本空间是Ω={(12) , (13), (14) ,(15) ,(23), (24), (25), (34) ,(35) ,(45)}∴n=10用A来表示“两数都是奇数”这一事件,则A={(13),(15),(3,5)}∴m=3∴P(A)=偶数呢?一个是奇数,一个是偶数呢?例2:豌豆的高矮性状的遗传由一对基因决定,其中决定高的基因记为D,决定矮的基因记为d,则杂交所得第一代的一对基因为Dd。若第二子代的D,d基因的遗传是等可能的,求第二子代为高茎的概率(只要有基因D则其就是高茎,只有两个基因全是d时,才显现矮茎)解:Dd与Dd的搭配方式有四种:DD,Dd,dD,dd,其中只有第四种表现为矮茎,故第二子代为高茎的概率为3/4=75%
答:第二子代为高茎的概率为75%一.选择题
1.某班准备到郊外野营,为此向商店订了帐篷。如果下雨与不下雨是等可能的,能否准时收到帐篷也是等可能的。只要帐篷如期运到,他们就不会淋雨,则下列说法中,正确的是( )
A 一定不会淋雨 B 淋雨机会为3/4
C 淋雨机会为1/2 D 淋雨机会为1/4
E 必然要淋雨D课堂练习二.填空题
1.一年按365天算,2名同学在同一天过生日的概率为____________
2.一个密码箱的密码由5位数字组成,五个数字都可任意设定为0-9中的任意一个数字,假设某人已经设定了五位密码。
(1)若此人忘了密码的所有数字,则他一次就能把锁打开的概率为____________
(2)若此人只记得密码的前4位数字,则一次就能把锁打开的概率____________ 1/1000001/101/365小 结本节主要研究了古典概型的概率求法,解题时要注意两点:
(1)古典概型的使用条件:试验结果的有限性和所有结果的等可能性。
(2)古典概型的解题步骤;
①求出总的基本事件数;
②求出事件A所包含的基本事件数,然后利
用公式P(A)=
互斥事件是指事件A与事件B在一次试验中不会同
时发生,其具体包括三种不同的情形:
(1)事件A发生且事件B不发生;
(2)事件A不发生且事件B发生;
(3)事件A与事件B同时不发生,
对立事件是指事件A与事件B有且仅有一个发生,
其包括两种情形:
(1)事件A发生B不发生;
(2)事件B发生事件A不发生,
对立事件是互斥事件的特殊情形。
AB对于随机事件,我们是否只
能通过大量重复试验才能求
其概率呢?有的情况下的大量重复的试验是否可以避免?问题1:抛一枚均匀的硬币,可能出现的结果有:由于硬币是均匀的,可以认为出现这2种结果的可能性是,.这与大量重复试验的结果是一致的. 出现“反面向上”的概率也是正面向上反面向上相等的即可以认为出现“正面向上”的概率是
问题2:抛掷一个骰子,它落地时向上的数可能是……也就是说,出现每一种结果的概率都是这种分析也与大量重复试验的结果是一致的. 即可能出现的结果有6种,且每种结果出现的机会是可能是情形1,2,3,4,5,6之一.
均等的(因为骰子是均匀的)问:什么样的事件的概率可以不通过重复试验,而通过对一次试验中可能出现的结果的分析来计算其概率呢?(1)所有结果出现的可能性都相等(2)所出现的结果是有限的⑴基本事件:一次试验中可能出现的每一个基本结果.如抛掷硬币的试验中,由2个基本事件组成。抛掷一个均
匀的骰子的试验中,由6个基本事件组成。 如果一次试验由n个基本事件组成,而且所有的基本事件
出现 的可能性都相等,那么每一个基本事件的概率都是 1/n 。事件A:试验中的一个事件,它由一个或几个基本事件构成。(2)等可能事件:通过以上两个例子进行归纳: 我们将满足(1)(2)两个条件的随机试验的概率模型成为古典概型。
由于以上这些都是历史上最早研究的概率模型,
对上述的数学模型我们称为古典概型 。(1)所有的基本事件只有有限个。(2)每个基本事件的发生都是等可能的。 (1)向一个圆面内随机地投射一个点,如果该点落在圆内任意一点都是等可能的,你认为这是古典概型吗?为什么? (2)如图,某同学随机地向一靶心进行射击,这一试验的结果只有有限个:命中10环、命中9环……命中5环和不中环。你认为这是古典概型吗?为什么? 因为试验的所有可能结果是圆面内所有的点,试验的所有可能结果数是无限的,虽然每一个试验结果出现的“可能性相同”,但这个试验不满足古典概型的第一个条件。 不是古典概型,因为试验的所有可能结果只有7个,而命中10环、命中9环……命中5环和不中环的出现不是等可能的,即不满足古典概型的第二个条件。 问题:抛掷一个骰子,求骰子落地时向上的数是三的倍数的概率是多少呢? 如果某个事件A包含了其中m个等可能基本事件,那么事件A的概率古典概型的概率应用:掷一颗质地均匀的骰子,观察掷出的点数,
(1)写出所有的基本事件,说明其是否是古典概型。 解:有6个基本事件,分别是“出现1点”,“出现2点”,……,“出现6点”。因为骰子的质地均匀,所以每个基本事件的发生是等可能的,因此它是古典概型。(2)观察掷出的点数,求掷得奇数点的概率。 解:这个试验的基本事件共有6个,即(出现1点)、(出现2点)……、(出现6点)
所以基本事件数n=6,
事件A=(掷得奇数点)=(出现1点,出现3点,出现5点),
其包含的基本事件数m=3 所以,P(A)=0.5(1,2)(1,3)(1,4)(1,5)
(2,3)(2,4)(2,5)
(3,4)(3,5)
(4,5)
因此,共有10个基本事件
(2)记摸到2只白球的事件为事件A,
即(1,2)(1,3)(2,3)故P(A)= 3/10 例1 一只口袋内装有大小相同的5只球,其中3只白球,2只红球,从中一次摸出两只球(1)共有多少基本事件(2)摸出的两只球都是白球的概率是多少?解:(1)分别记白球1,2,3号,红球为4,5号,从中摸出2只球,有如下基本事件(摸到1,2号球用(1,2)表示):(3) 该事件可用Venn图表示在集合I中共有10个元素
在集合A中有3个元素
故P(A)= 3/10变式(3)所取的2个球中都是红球的概率是 ?
(4)取出的两个球一白一红的概率是?解:(3)则基本事件仍为10个,其中两个球都是红球的事件包括1个基本事件,所以,所求事件的概率为解:(4)则基本事件仍为10个,其中取出的两个球一白一红的的事件包括6个基本事件,所以,所求事件的概率为求古典概型的步骤:(1)判断是否为等可能性事件;
(2)计算所有基本事件的总结果数n.
(3)计算事件A所包含的结果数m.
(4)计算 概 率 初 步变式?1、从1,2, 3,4, 5五个数字中,任取两数,求两数都是奇数的概率。解:试验的样本空间是Ω={(12) , (13), (14) ,(15) ,(23), (24), (25), (34) ,(35) ,(45)}∴n=10用A来表示“两数都是奇数”这一事件,则A={(13),(15),(3,5)}∴m=3∴P(A)=偶数呢?一个是奇数,一个是偶数呢?例2:豌豆的高矮性状的遗传由一对基因决定,其中决定高的基因记为D,决定矮的基因记为d,则杂交所得第一代的一对基因为Dd。若第二子代的D,d基因的遗传是等可能的,求第二子代为高茎的概率(只要有基因D则其就是高茎,只有两个基因全是d时,才显现矮茎)解:Dd与Dd的搭配方式有四种:DD,Dd,dD,dd,其中只有第四种表现为矮茎,故第二子代为高茎的概率为3/4=75%
答:第二子代为高茎的概率为75%一.选择题
1.某班准备到郊外野营,为此向商店订了帐篷。如果下雨与不下雨是等可能的,能否准时收到帐篷也是等可能的。只要帐篷如期运到,他们就不会淋雨,则下列说法中,正确的是( )
A 一定不会淋雨 B 淋雨机会为3/4
C 淋雨机会为1/2 D 淋雨机会为1/4
E 必然要淋雨D课堂练习二.填空题
1.一年按365天算,2名同学在同一天过生日的概率为____________
2.一个密码箱的密码由5位数字组成,五个数字都可任意设定为0-9中的任意一个数字,假设某人已经设定了五位密码。
(1)若此人忘了密码的所有数字,则他一次就能把锁打开的概率为____________
(2)若此人只记得密码的前4位数字,则一次就能把锁打开的概率____________ 1/1000001/101/365小 结本节主要研究了古典概型的概率求法,解题时要注意两点:
(1)古典概型的使用条件:试验结果的有限性和所有结果的等可能性。
(2)古典概型的解题步骤;
①求出总的基本事件数;
②求出事件A所包含的基本事件数,然后利
用公式P(A)=
