高二数学期末复习试卷
图片预览


文档简介
高二文科期末复习题(四)
一、选择题
1、已知动点M的坐标满足方程,则动点M的轨迹是( )
A.椭圆 B.双曲线 C.抛物线 D.其他图形
2、已知F1、F2是椭圆的两焦点,过点F2的直线交椭圆于点A、B,若|AB|=5,则|AF1|-|BF2|=( )
A.3 B.8 C.13 D.16
3、无论为何值,方程所表示的曲线必不是( )
A.双曲线 B.抛物线 C.椭圆 D.圆
4、设抛物线的焦点为F,准线为,P为抛物线上一点,,A为垂足,如果直线AF的斜率为,那么|PF|=( )
A. B.8 C. D.16
5、设F1、F2分别为双曲线的左、右焦点,若在双曲线右支上存在点P,满足|PF2|=|F1F2|,且F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )
A. B. C. D.
6、若点O和F分别为椭圆的中心和左焦点,点P为椭圆上任意一点,则的最大值为( )
A.2 B.3 C.6 D.8
7、如果椭圆被点平分,则这条弦所在的直线方程为( )
A. B. C. D.
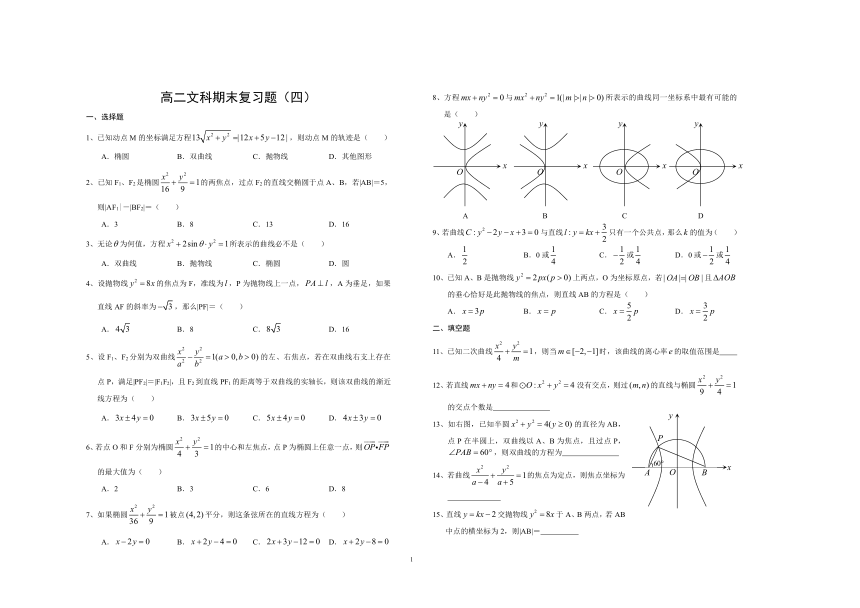
8、方程与所表示的曲线同一坐标系中最有可能的是( )
A B C D
9、若曲线与直线只有一个公共点,那么的值为( )
A. B.0或 C.或 D.0或或
10、已知A、B是抛物线上两点,O为坐标原点,若且的垂心恰好是此抛物线的焦点,则直线AB的方程是( )
A. B. C. D.
二、填空题
11、已知二次曲线,则当时,该曲线的离心率的取值范围是
12、若直线和没有交点,则过的直线与椭圆 的交点个数是
13、如右图,已知半圆的直径为AB,点P在半圆上,双曲线以A、B为焦点,且过点P,,则双曲线的方程为
14、若曲线的焦点为定点,则焦点坐标为
15、直线交抛物线于A、B两点,若AB中点的横坐标为2,则|AB|=
三、解答题
16、已知抛物线,焦点为F,顶点为O,点P在抛物线上移动,Q是OP中点,M是FQ中点,求点M的轨迹方程。
17、已知直线交椭圆于M、N两点,是椭圆的一个顶点,若的重心恰好是椭圆的右焦点,求直线的方程。
18、求两条渐近线为,且截直线所得弦长为的双曲线方程。
19、某工程需将水平直线的公路下侧的土石,通过公路上的两个道口A和B,沿着道路AP,BP运往公路上侧的P处,PA=100m,PB=150m,,试说明怎样运土石最省工?
20、如图,直线与抛物线交于两点,与轴相交于点M,且
⑴求证:M点的坐标为;
⑵求证:;
⑶求的面积的最小值。
21、设是椭圆上两点,已知向量,若且椭圆离心率,短轴长为2,O为坐标原点
⑴求椭圆方程;
⑵若直线AB斜率存在且直线AB过椭圆的焦点(为半焦距),求直线AB的斜率的值;
⑶试问:的面积是否为定值?如果是,请给予证明,如果不是,请说明理由。
高二文科期末复习题(四)答题卷
第Ⅰ卷 (选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.请填入下面表格中.
题 号
1
2
3
4
5
6
7
8
9
10
答 案
第Ⅱ卷 (非选择题 共100分)
二、填空题:本大题共5小题,每小题5分,满分25分.把正确答案填在题中相应的横线上.
11、 12、
13、 14、
15、
三、解答题:本大题共6小题,共75分.解答应写出必要的文字说明、证明过程或演算步骤.
16、(本小题满分12分)
解:
17、(本小题满分12分)
解:
18、(本小题满分12分)
解:
19、(本小题满分12分)
解:
20、(本小题满分13分)
解:
21、(本小题满分14分)
解:
高二文科期末复习题(四)参考答案
一、选择题
1-5 CABBD 6-10 CDADC
二、填空题
11、 12、2 13、 14、 15、
三、解答题
16、解:设
易知的焦点F为
M是FQ中点
又Q是OP中点
点P在抛物线上
M点的轨迹方程为
17、解:椭圆的右焦点为,设,
则
又过MN的中点
的方程为即
18、解:设双曲线方程为
联立方程组得: 消去得
设直线被双曲线截得的弦为AB,且
那么
满足
所求的双曲线方程是
19、解:以直线为轴,线段AB的中点为原点建立平面直角坐标系,则在一侧必存在经A到P到与经B到P路程相等的点,设这样的点为M,则
|MA|+|AP|=|MB|+|BP|
即|MA|-|MB|=|BP|-|AP|=50
又
M在双曲线的右支上
故曲线右侧的土石经道口B沿BP运往P处,曲线左侧的土石经道口A沿AP运往P处,按这种方法运土石最省工。
20、解:⑴设M点坐标为,直线的方程为
代入得
是此方程的两根
M点坐标为
⑵
⑶由⑴可知 且
于是
当时,的面积取最小值1
21、解:⑴由题意知
椭圆方程为
⑵由题意设直线AB的方程为
由 得
由得
解得
⑶(i)当直线AB斜率不存在时,而,由
得 即
又在椭圆上
面积为定值
(ii)当直线AB斜率存在时,设直线AB方程为
由 消去得
则
由得
整理得
的面积为定值
一、选择题
1、已知动点M的坐标满足方程,则动点M的轨迹是( )
A.椭圆 B.双曲线 C.抛物线 D.其他图形
2、已知F1、F2是椭圆的两焦点,过点F2的直线交椭圆于点A、B,若|AB|=5,则|AF1|-|BF2|=( )
A.3 B.8 C.13 D.16
3、无论为何值,方程所表示的曲线必不是( )
A.双曲线 B.抛物线 C.椭圆 D.圆
4、设抛物线的焦点为F,准线为,P为抛物线上一点,,A为垂足,如果直线AF的斜率为,那么|PF|=( )
A. B.8 C. D.16
5、设F1、F2分别为双曲线的左、右焦点,若在双曲线右支上存在点P,满足|PF2|=|F1F2|,且F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )
A. B. C. D.
6、若点O和F分别为椭圆的中心和左焦点,点P为椭圆上任意一点,则的最大值为( )
A.2 B.3 C.6 D.8
7、如果椭圆被点平分,则这条弦所在的直线方程为( )
A. B. C. D.
8、方程与所表示的曲线同一坐标系中最有可能的是( )
A B C D
9、若曲线与直线只有一个公共点,那么的值为( )
A. B.0或 C.或 D.0或或
10、已知A、B是抛物线上两点,O为坐标原点,若且的垂心恰好是此抛物线的焦点,则直线AB的方程是( )
A. B. C. D.
二、填空题
11、已知二次曲线,则当时,该曲线的离心率的取值范围是
12、若直线和没有交点,则过的直线与椭圆 的交点个数是
13、如右图,已知半圆的直径为AB,点P在半圆上,双曲线以A、B为焦点,且过点P,,则双曲线的方程为
14、若曲线的焦点为定点,则焦点坐标为
15、直线交抛物线于A、B两点,若AB中点的横坐标为2,则|AB|=
三、解答题
16、已知抛物线,焦点为F,顶点为O,点P在抛物线上移动,Q是OP中点,M是FQ中点,求点M的轨迹方程。
17、已知直线交椭圆于M、N两点,是椭圆的一个顶点,若的重心恰好是椭圆的右焦点,求直线的方程。
18、求两条渐近线为,且截直线所得弦长为的双曲线方程。
19、某工程需将水平直线的公路下侧的土石,通过公路上的两个道口A和B,沿着道路AP,BP运往公路上侧的P处,PA=100m,PB=150m,,试说明怎样运土石最省工?
20、如图,直线与抛物线交于两点,与轴相交于点M,且
⑴求证:M点的坐标为;
⑵求证:;
⑶求的面积的最小值。
21、设是椭圆上两点,已知向量,若且椭圆离心率,短轴长为2,O为坐标原点
⑴求椭圆方程;
⑵若直线AB斜率存在且直线AB过椭圆的焦点(为半焦距),求直线AB的斜率的值;
⑶试问:的面积是否为定值?如果是,请给予证明,如果不是,请说明理由。
高二文科期末复习题(四)答题卷
第Ⅰ卷 (选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.请填入下面表格中.
题 号
1
2
3
4
5
6
7
8
9
10
答 案
第Ⅱ卷 (非选择题 共100分)
二、填空题:本大题共5小题,每小题5分,满分25分.把正确答案填在题中相应的横线上.
11、 12、
13、 14、
15、
三、解答题:本大题共6小题,共75分.解答应写出必要的文字说明、证明过程或演算步骤.
16、(本小题满分12分)
解:
17、(本小题满分12分)
解:
18、(本小题满分12分)
解:
19、(本小题满分12分)
解:
20、(本小题满分13分)
解:
21、(本小题满分14分)
解:
高二文科期末复习题(四)参考答案
一、选择题
1-5 CABBD 6-10 CDADC
二、填空题
11、 12、2 13、 14、 15、
三、解答题
16、解:设
易知的焦点F为
M是FQ中点
又Q是OP中点
点P在抛物线上
M点的轨迹方程为
17、解:椭圆的右焦点为,设,
则
又过MN的中点
的方程为即
18、解:设双曲线方程为
联立方程组得: 消去得
设直线被双曲线截得的弦为AB,且
那么
满足
所求的双曲线方程是
19、解:以直线为轴,线段AB的中点为原点建立平面直角坐标系,则在一侧必存在经A到P到与经B到P路程相等的点,设这样的点为M,则
|MA|+|AP|=|MB|+|BP|
即|MA|-|MB|=|BP|-|AP|=50
又
M在双曲线的右支上
故曲线右侧的土石经道口B沿BP运往P处,曲线左侧的土石经道口A沿AP运往P处,按这种方法运土石最省工。
20、解:⑴设M点坐标为,直线的方程为
代入得
是此方程的两根
M点坐标为
⑵
⑶由⑴可知 且
于是
当时,的面积取最小值1
21、解:⑴由题意知
椭圆方程为
⑵由题意设直线AB的方程为
由 得
由得
解得
⑶(i)当直线AB斜率不存在时,而,由
得 即
又在椭圆上
面积为定值
(ii)当直线AB斜率存在时,设直线AB方程为
由 消去得
则
由得
整理得
的面积为定值
同课章节目录
