数学(北师大版):《抛物线过焦点弦性质》课件
文档属性
| 名称 | 数学(北师大版):《抛物线过焦点弦性质》课件 |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-01-18 18:02:00 | ||
图片预览






文档简介
课件17张PPT。抛物线过焦点弦的性质及应用萧城一中: 孙鑫
2011年1月11号 星期二复习回顾抛物线性质:
1,抛物线定义
2,抛物线几何性质
关于x 轴
对称,无
对称中心关于x 轴
对称,无
对称中心关于y 轴
对称,无
对称中心关于y 轴
对称,无
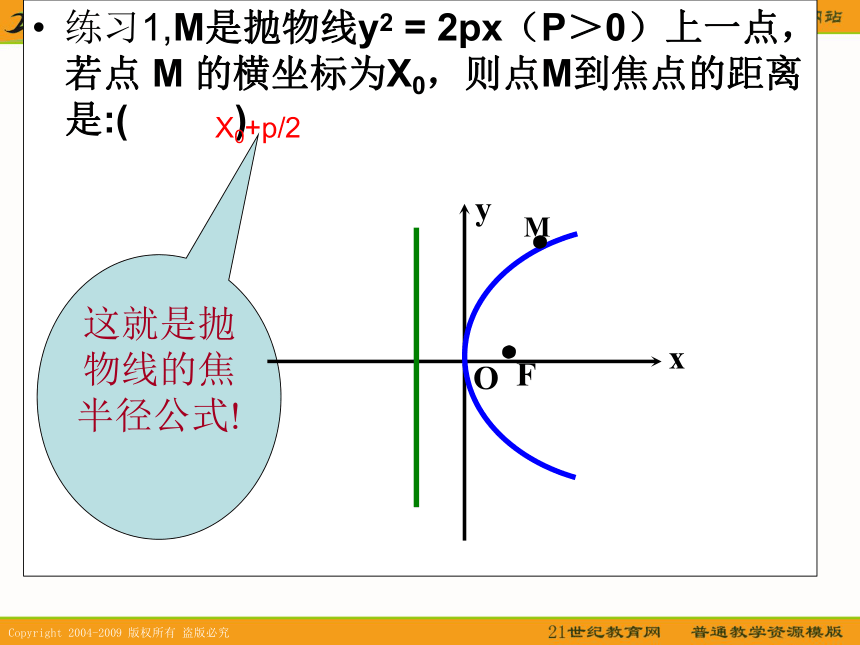
对称中心e=1e=1e=1e=1练习1,M是抛物线y2 = 2px(P>0)上一点,若点 M 的横坐标为X0,则点M到焦点的距离是:( )
这就是抛物线的焦半径公式!X0+p/2 过焦点弦与抛物线交点坐标关系 例1:已知F是抛物线y2=6x的焦点,过焦点任作直线交抛物线与A(x1,y1),B(x2,y2)两点 ①当直线的斜率k=1时,求 x1x2, y1y2的值 ②当直线的斜率k=2时,求 x1x2, y1y2的值上面结果是巧合吗?分析:关键是联立方程组,利用根与系数的关系求解。解:①x1x2=_____
y1y2=_____
② x1x2=_____
y1y2=______ 已知F是抛物线y2=2px(p>0)的焦点,过焦点任作直线交抛物线与A(x1,y1),B(x2,y2)两点
证明: x1x2=
y1y2= 过焦点弦长问题例2:过抛物线y2=4x的
焦点作倾斜角为45度的
直线交抛物线与A,B
两点,求∣AB∣
分析,求出A,B两点坐标,然后利用两点间的距离公式可得∣AB∣
解(法一)由条件可得F(1,0)
则直线的方程为:y=x-1
由
可得
解得
由两点距离公式可得∣AB∣=8
(法二)利用方程,利用弦长公式同样可的∣AB∣=8 分析:利用抛物线性质解决问题
解(法三)如图可知设A(x1,y1),B(x2,y2)
∣AB∣=∣AF∣+∣BF∣
=x1+1+x2+1
=x1+x2+1+1
由上知x1,x2是方程
的两根,故x1+x2=6,所以
∣AB∣=6+2=8一般的:若过抛物线y2=2px(p>0)的焦点的直线交抛物线A(x1,y1),B(x2,y2)两点,则
1,∣AB∣有最小值吗?
若有又为多少?
2,对于其他标准方程,你能
写出过焦点弦长公式吗?F通径:通过焦点且垂直对称轴
的直线,与抛物线相交于两点,
连接这两点的线段叫做抛物线
的通径。
通径的长度为 :
此是 2p的几何意义。AB2p例3:设F是抛物线G:x2=4y的焦点,A,B为G上异于原点的两点,且满足 的两点,延长AF,BF分别交抛物线G与C,D ,求 四边形ABCD面积的最小值
x分析:解此题的关键是把四边形面积表示出来
解:如图设直线AC的斜率为k则k≠0
由条件可知直线AC方程为y=kx+1
联立方程组
可得
故xA+xC=4k
所以︱AC︱=yA+yC+2=k(xA+xC)+4
=4k2+4
同理可得︱BD︱=4(1/k2+1)
故 SABCD=
(当且仅当k2=1时取=) 1,长为8的线段AB两端点在抛物线 y2=6x上运动,求AB中点M到抛物线准
线的最近距离。( )
2,过抛物线焦点F的直线交抛物线
于A,B两点,通过点A和抛物线顶点
的直线交抛物线的 准线于点D,
求证:直线DB平行于抛物
线的对称轴。
4咱来试一试
小结:
1,过抛物线焦点弦与抛物线交点 坐标关系
2,过抛物线交点弦的弦长问题
及应用
P76,7,9,10
作 业谢谢大家,再见!
2011年1月11号 星期二复习回顾抛物线性质:
1,抛物线定义
2,抛物线几何性质
关于x 轴
对称,无
对称中心关于x 轴
对称,无
对称中心关于y 轴
对称,无
对称中心关于y 轴
对称,无
对称中心e=1e=1e=1e=1练习1,M是抛物线y2 = 2px(P>0)上一点,若点 M 的横坐标为X0,则点M到焦点的距离是:( )
这就是抛物线的焦半径公式!X0+p/2 过焦点弦与抛物线交点坐标关系 例1:已知F是抛物线y2=6x的焦点,过焦点任作直线交抛物线与A(x1,y1),B(x2,y2)两点 ①当直线的斜率k=1时,求 x1x2, y1y2的值 ②当直线的斜率k=2时,求 x1x2, y1y2的值上面结果是巧合吗?分析:关键是联立方程组,利用根与系数的关系求解。解:①x1x2=_____
y1y2=_____
② x1x2=_____
y1y2=______ 已知F是抛物线y2=2px(p>0)的焦点,过焦点任作直线交抛物线与A(x1,y1),B(x2,y2)两点
证明: x1x2=
y1y2= 过焦点弦长问题例2:过抛物线y2=4x的
焦点作倾斜角为45度的
直线交抛物线与A,B
两点,求∣AB∣
分析,求出A,B两点坐标,然后利用两点间的距离公式可得∣AB∣
解(法一)由条件可得F(1,0)
则直线的方程为:y=x-1
由
可得
解得
由两点距离公式可得∣AB∣=8
(法二)利用方程,利用弦长公式同样可的∣AB∣=8 分析:利用抛物线性质解决问题
解(法三)如图可知设A(x1,y1),B(x2,y2)
∣AB∣=∣AF∣+∣BF∣
=x1+1+x2+1
=x1+x2+1+1
由上知x1,x2是方程
的两根,故x1+x2=6,所以
∣AB∣=6+2=8一般的:若过抛物线y2=2px(p>0)的焦点的直线交抛物线A(x1,y1),B(x2,y2)两点,则
1,∣AB∣有最小值吗?
若有又为多少?
2,对于其他标准方程,你能
写出过焦点弦长公式吗?F通径:通过焦点且垂直对称轴
的直线,与抛物线相交于两点,
连接这两点的线段叫做抛物线
的通径。
通径的长度为 :
此是 2p的几何意义。AB2p例3:设F是抛物线G:x2=4y的焦点,A,B为G上异于原点的两点,且满足 的两点,延长AF,BF分别交抛物线G与C,D ,求 四边形ABCD面积的最小值
x分析:解此题的关键是把四边形面积表示出来
解:如图设直线AC的斜率为k则k≠0
由条件可知直线AC方程为y=kx+1
联立方程组
可得
故xA+xC=4k
所以︱AC︱=yA+yC+2=k(xA+xC)+4
=4k2+4
同理可得︱BD︱=4(1/k2+1)
故 SABCD=
(当且仅当k2=1时取=) 1,长为8的线段AB两端点在抛物线 y2=6x上运动,求AB中点M到抛物线准
线的最近距离。( )
2,过抛物线焦点F的直线交抛物线
于A,B两点,通过点A和抛物线顶点
的直线交抛物线的 准线于点D,
求证:直线DB平行于抛物
线的对称轴。
4咱来试一试
小结:
1,过抛物线焦点弦与抛物线交点 坐标关系
2,过抛物线交点弦的弦长问题
及应用
P76,7,9,10
作 业谢谢大家,再见!
