3.2立体几何中的向量方法(二)
文档属性
| 名称 | 3.2立体几何中的向量方法(二) |

|
|
| 格式 | rar | ||
| 文件大小 | 609.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-01-22 00:00:00 | ||
图片预览





文档简介
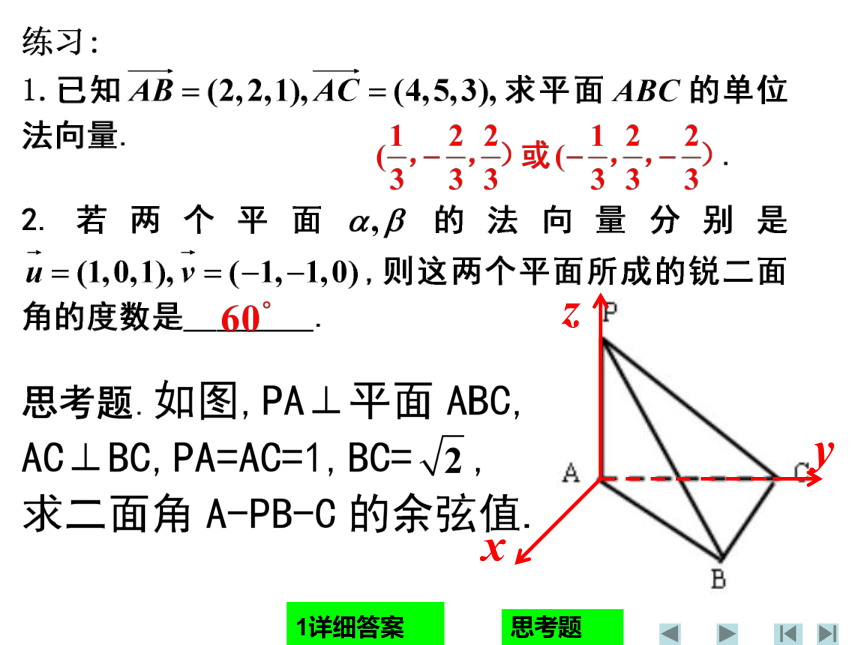
课件15张PPT。练习巩固思考1引入知识要点例1的思考方法小结练习巩固1详细答案思考题1答案方法小结(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题(还常建立坐标系来辅助);(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;(3)把向量的运算结果“翻译”成相应的几何意义.(化为向量问题或向量的坐标问题)(进行向量运算)(回到图形)课外思考(1)(2)(3) 例1:如图1:一个结晶体的形状为四棱柱,其中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°,那么以这个顶点为端点的晶体的对角线的长与棱长有什么关系? 解:如图1,不妨设化为向量问题依据向量的加法法则,进行向量运算所以回到图形问题这个晶体的对角线 的长是棱长的 倍。思考:(1)本题中四棱柱的对角线BD1的长与棱长有什么关系? (2)如果一个四棱柱的各条棱长都相等,并且以某一顶点为端点的各棱间的夹角都等于 , 那么有这个四棱柱的对角线的长可以确定棱长吗? (3)本题的晶体中相对的两个平面之间的距离
是多少? (提示:求两个平行平面的距离,通常归结为求点到平面的距离或两点间的距离)思考(1)分析:思考(2)分析:∴ 这个四棱柱的对角线的长可以确定棱长.思考(3)下一节分析H 分析:面面距离转化为点面距离来求解:∴ 所求的距离是 思考(3)本题的晶体中相对的两个平面之间的距离是多少? 如何用向量法求点到平面的距离?DABCGFE如何用向量法求点到平面的距离?DABCGFE
是多少? (提示:求两个平行平面的距离,通常归结为求点到平面的距离或两点间的距离)思考(1)分析:思考(2)分析:∴ 这个四棱柱的对角线的长可以确定棱长.思考(3)下一节分析H 分析:面面距离转化为点面距离来求解:∴ 所求的距离是 思考(3)本题的晶体中相对的两个平面之间的距离是多少? 如何用向量法求点到平面的距离?DABCGFE如何用向量法求点到平面的距离?DABCGFE
