3.2立体几何中的向量方法(四)
文档属性
| 名称 | 3.2立体几何中的向量方法(四) |

|
|
| 格式 | rar | ||
| 文件大小 | 702.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-01-22 00:00:00 | ||
图片预览





文档简介
课件15张PPT。求两点间的距离课本例3引入例1的思考(3)再尝试练习3课本例2的学习 课本第116页练习2的思考:(求两点间的距离向量法思路)
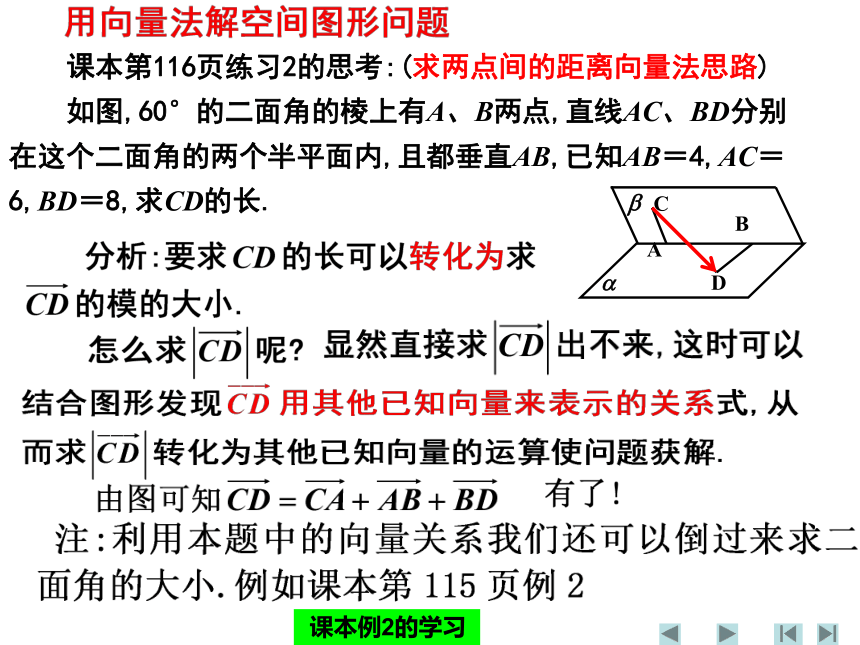
如图,60°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直AB,已知AB=4,AC=6,BD=8,求CD的长. 第115页的思考解答(由学生课外学习)分析:如图,化为向量问题由图可知有向量关系进行向量运算尝试课本第115页例2的思考(2)
如果已知一个四棱柱的各棱长和一条对角线的长,并且以同一顶点为端点的各棱间的夹角都相等,那么可以确定各棱之间夹角的余弦值吗? 分析:如图,设以顶点 为端点的对角线
长为 ,三条棱长分别为 各棱间夹角为 。则 课本第115页的思考(3)
如果已知一个四棱柱的各棱长都等于 ,并且以某一顶点为端点的各棱间的夹角都等于 ,那么可以确定这个四棱柱相邻两个面夹角的余弦值吗?A1B1C1D1ABCD分析:二面角平面角向量的夹角回归图形 解:如图,在平面 AB1 内过 A1 作
A1E⊥AB 于点 E,EF在平面 AC 内作 CF⊥AB 于 F。∴可以确定这个四棱柱相邻两个夹角的余弦值。向量法(坐标化)不建坐标系怎么解1答案2答案所以:CABCC1EA1B1
如图,60°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直AB,已知AB=4,AC=6,BD=8,求CD的长. 第115页的思考解答(由学生课外学习)分析:如图,化为向量问题由图可知有向量关系进行向量运算尝试课本第115页例2的思考(2)
如果已知一个四棱柱的各棱长和一条对角线的长,并且以同一顶点为端点的各棱间的夹角都相等,那么可以确定各棱之间夹角的余弦值吗? 分析:如图,设以顶点 为端点的对角线
长为 ,三条棱长分别为 各棱间夹角为 。则 课本第115页的思考(3)
如果已知一个四棱柱的各棱长都等于 ,并且以某一顶点为端点的各棱间的夹角都等于 ,那么可以确定这个四棱柱相邻两个面夹角的余弦值吗?A1B1C1D1ABCD分析:二面角平面角向量的夹角回归图形 解:如图,在平面 AB1 内过 A1 作
A1E⊥AB 于点 E,EF在平面 AC 内作 CF⊥AB 于 F。∴可以确定这个四棱柱相邻两个夹角的余弦值。向量法(坐标化)不建坐标系怎么解1答案2答案所以:CABCC1EA1B1
