2011届上海市黄浦区高三第一学期期终基础学业测评数学理卷
文档属性
| 名称 | 2011届上海市黄浦区高三第一学期期终基础学业测评数学理卷 |  | |
| 格式 | rar | ||
| 文件大小 | 177.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-01-22 14:21:00 | ||
图片预览




文档简介
黄浦区2010学年度第一学期期终基础学业测评
高三数学试卷(理)
(2011年1月12日)
考生注意:
1.每位考生应同时收到试卷和答题卷两份材料,解答必须在答题卷上进行,写在试卷上的解答一律无效;
2.答卷前,考生务必将姓名、准考证号等相关信息在答题卷上填写清楚;
3.本试卷共23道试题,满分150分;考试时间120分钟.
一.填空题(本大题满分56分) 本大题共有14题,考生应在答题卷的相应编号的空格内直接填写结果,每题填对得4分,否则一律得零分.
1.函数的定义域是 .
2.已知函数互为反函数,若函数
的图像过点,则= .
3.已知命题A:若.命题A的逆否命题是 ;该逆否命题是 .(填“真命题”或“假命题”)
4.已知全集,集合,
,则= .
5.不等式的解集是 .
6.方程的解集是 .
7.已知角的顶点在原点,始边与平面直角坐标系x轴的正半轴重合,点在角的终边上,则= .
8.如图1所示,正三棱柱的所有棱的长度都为4,则异面直线所成的角是 (结果用反三角函数值表示).
9.已知某圆锥体的底面半径,沿圆锥体的母线把侧面展开后可得到圆心角为的扇形,则该圆锥体的体积是 .
10.已知是两个不共线的平面向量,向量,若,则= .
11.一副扑克牌(有四色,同一色有13张不同牌)共52张.现随机抽取3张牌,则抽出的3张牌有且仅有2张花色相同的概率为 (用数值作答).
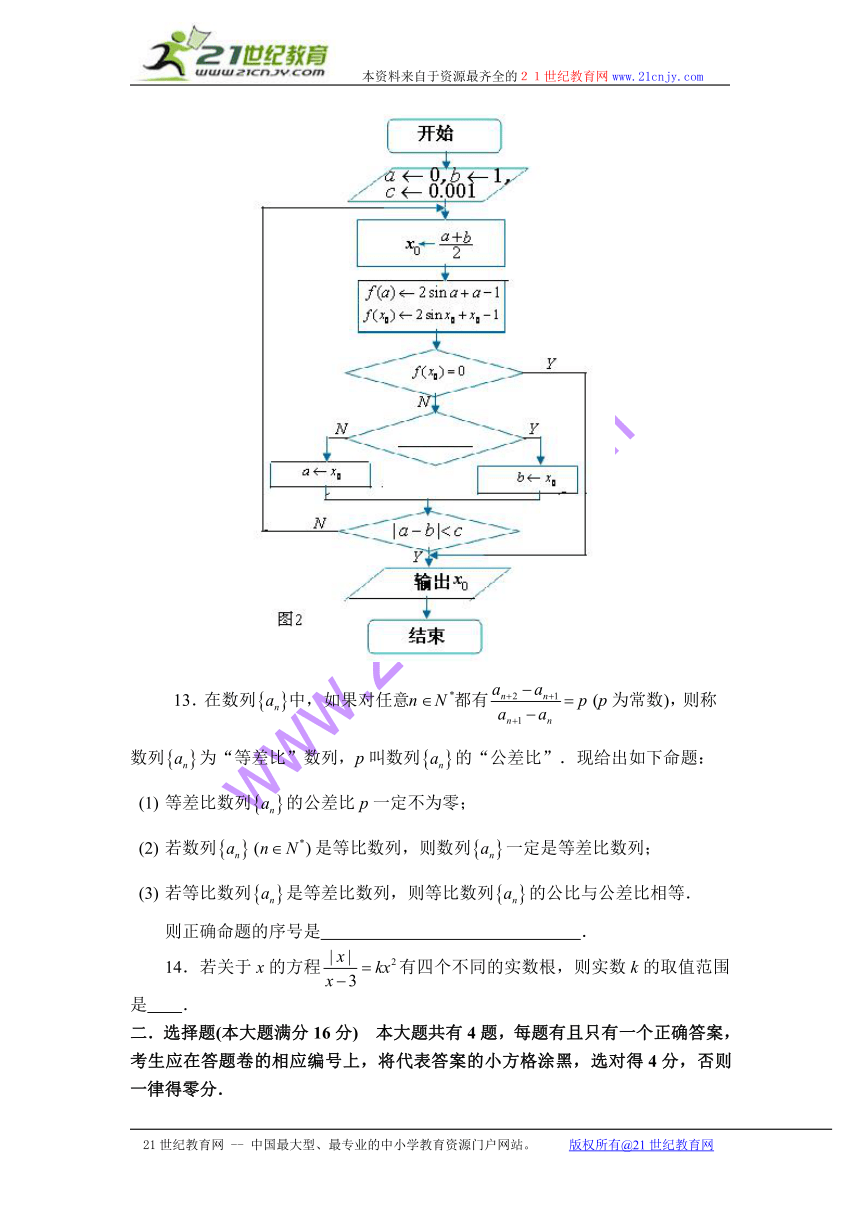
12.下面是用区间二分法求方程在内的一个近似解(误差不超过0.001)的算法框图,如图2所示,则判断框内空白处应填入 ,才能得到需要的解.
13.在数列(p为常数),则称数列为“等差比”数列,p叫数列的“公差比”.现给出如下命题:
等差比数列的公差比p一定不为零;
若数列是等比数列,则数列一定是等差比数列;
若等比数列是等差比数列,则等比数列的公比与公差比相等.
则正确命题的序号是 .
14.若关于x的方程有四个不同的实数根,则实数k的取值范围是 .
二.选择题(本大题满分16分) 本大题共有4题,每题有且只有一个正确答案,考生应在答题卷的相应编号上,将代表答案的小方格涂黑,选对得4分,否则一律得零分.
15.函数()的最小正周期T= [答]( )
A.. B.. C.. D..
16.已知关于x、y的二元一次线性方程组的增广矩阵是,则该线性方程组有无穷多组解的充要条件是= [答]( )
A.2. B.1或2. C.1. D.0.
17.给出下列命题:
(1)函数
(2) ;
(3)在空间中,若角的两边分别与角的两边平行,则;
(4)从总体中通过科学抽样得到样本数据(),则数值(为样本平均值)可作为总体标准差的点估计值.
则上述命题正确的序号是 [答]( )
A.(1)、(2)、(4). B.(4). C.(2)、(3). D.(2)、(4).
18.若,则该数列的前2011项的乘积 [答]( )
A.3. B.-6. C.. D..
三.解答题(本大题满分78分)本大题共有5题,解答下列各题必须在答题卷的相应编号规定区域内写出必要的步骤.
19.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
如图3所示,已知三棱锥中,点
的中点.
(1)求证四点共面;
(2)已知,点C在球面上,求球M的体积V.
20.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
定义:如果函数,满足
,则称函数是上的“平均值函数”,是它的一个均值点.如上的平均值函数,0就是它的均值点.
(1)判断函数在区间上是否为平均值函数?若是,求出它的均值点;若不是,请说明理由;
(2)若函数上的平均值函数,试确定实数的取值范围.
21.(本题满分16分)本题共有2个小题,第1小题满分7分,第2小题满分9分.
已知是偶函数.
求b的值;
若在函数定义域内总存在区间(m22.(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.
如图4,某市拟在长为16km的道路OP的一侧修建一条自行车赛道,赛道的前一部分为曲线OSM,该曲线段为函数的图像,且图像的最高点为.赛道的后一段为折线段MNP,为保证参赛队员的安全,限定.
(1)求实数的值以及M、P两点之间的距离;
(2)联结MP,设,试求出用的解析式;
(3)应如何设计,才能使折线段MNP最长?
23.(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分7分,第3小题满分5分.
已知各项都为正数的数列,其中的前n项的和.
(1);
(2)已知p(2)是给定的某个正整数,数列
(),求;
(3)化简.
黄浦区2010学年度第一学期期终基础学业测评
数学试卷(文理合卷)
(2011年1月12日)
参考答案和评分标准
一、填空题
1、;2、;3、 (每空2分) ;
4、;5、; 6、;
7、 ;8、(理科),(文科);9、 ;10、 ;
11、(理科),(文科);12、;
13、(理科)(1)、(3) ,(文科) ; 14、(理科),(文科) 3.
二、选择题: 15、B 16、C 17、D 18、(理科)A(文科)D
三、解答题
19、(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
解(1)
.
.
于是,.
(2)
.
.
.
.
.
20.(本题满分14分) 本题共有2个小题,第1小题满分7分,第2小题满分7分.
解(1)由定义可知,关于x的方程在内有实数根时,
函数.
解,可得.
又,
所以,上的平均值函数,5是它的均值点.
(2)上的平均值函数,
在内有实数根.
,解得.
又
必为均值点,即.
∴所求实数.
21.(本题满分16分)本题共有2个小题,第1小题满分7分,第2小题满分9分.
解(1)由已知可得,,且函数的定义域为D=.
又是偶函数,故定义域D关于原点对称.
于是,b=0().
又对任意
因此所求实数b=0.
(2) 由(1)可知,.
考察函数的图像,可知:
.
因在区间上的函数值组成的集合也是,故必有.
①当时,有,即方程,也就是有两个不相等的正实数根,因此,解得.
②当时,有,化简得,解得.
综上所述,所求实数.
22.(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.
解(1)结合题意和图像,可知,
解此方程组,得,于是.
进一步可得点M的坐标为.
所以,(km).
(2)在,故.
又,
因此,().
(3)把进一步化为:
().
所以,当(km).
可以这样设计:联结MP,分别过点M、P在MP的同一侧作与MP成角的射线,记两射线的交点为N,再修建线段NM和NP,就可得到满足要求的最长折线段MNP赛道.
23.(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分7分,第3小题满分5分.
(理科)解(1),,
.
.
是首项为,公差为2的等差数列;是首项为,公差为2的等差数列.又,可得.
∴.
所以,所求数列的通项公式为.
(2)是给定的正整数(),,
数列是项数为p项的有穷数列.又.
,…
归纳可得.
(3)由(2)可知,进一步可化为:.
所以,
.
(文科)
∴数列是等差比数列,且公差比p=2.
(2)∵数列是等差比数列,且公差比p=2,
,即数列.
.于是,
,
,
…
.
将上述个等式相加,得
.
∴数列的通项公式为.
(3)由(2)可知,
于是,.
所以,数列是等差比数列,且公差比为.
高三数学试卷(理)
(2011年1月12日)
考生注意:
1.每位考生应同时收到试卷和答题卷两份材料,解答必须在答题卷上进行,写在试卷上的解答一律无效;
2.答卷前,考生务必将姓名、准考证号等相关信息在答题卷上填写清楚;
3.本试卷共23道试题,满分150分;考试时间120分钟.
一.填空题(本大题满分56分) 本大题共有14题,考生应在答题卷的相应编号的空格内直接填写结果,每题填对得4分,否则一律得零分.
1.函数的定义域是 .
2.已知函数互为反函数,若函数
的图像过点,则= .
3.已知命题A:若.命题A的逆否命题是 ;该逆否命题是 .(填“真命题”或“假命题”)
4.已知全集,集合,
,则= .
5.不等式的解集是 .
6.方程的解集是 .
7.已知角的顶点在原点,始边与平面直角坐标系x轴的正半轴重合,点在角的终边上,则= .
8.如图1所示,正三棱柱的所有棱的长度都为4,则异面直线所成的角是 (结果用反三角函数值表示).
9.已知某圆锥体的底面半径,沿圆锥体的母线把侧面展开后可得到圆心角为的扇形,则该圆锥体的体积是 .
10.已知是两个不共线的平面向量,向量,若,则= .
11.一副扑克牌(有四色,同一色有13张不同牌)共52张.现随机抽取3张牌,则抽出的3张牌有且仅有2张花色相同的概率为 (用数值作答).
12.下面是用区间二分法求方程在内的一个近似解(误差不超过0.001)的算法框图,如图2所示,则判断框内空白处应填入 ,才能得到需要的解.
13.在数列(p为常数),则称数列为“等差比”数列,p叫数列的“公差比”.现给出如下命题:
等差比数列的公差比p一定不为零;
若数列是等比数列,则数列一定是等差比数列;
若等比数列是等差比数列,则等比数列的公比与公差比相等.
则正确命题的序号是 .
14.若关于x的方程有四个不同的实数根,则实数k的取值范围是 .
二.选择题(本大题满分16分) 本大题共有4题,每题有且只有一个正确答案,考生应在答题卷的相应编号上,将代表答案的小方格涂黑,选对得4分,否则一律得零分.
15.函数()的最小正周期T= [答]( )
A.. B.. C.. D..
16.已知关于x、y的二元一次线性方程组的增广矩阵是,则该线性方程组有无穷多组解的充要条件是= [答]( )
A.2. B.1或2. C.1. D.0.
17.给出下列命题:
(1)函数
(2) ;
(3)在空间中,若角的两边分别与角的两边平行,则;
(4)从总体中通过科学抽样得到样本数据(),则数值(为样本平均值)可作为总体标准差的点估计值.
则上述命题正确的序号是 [答]( )
A.(1)、(2)、(4). B.(4). C.(2)、(3). D.(2)、(4).
18.若,则该数列的前2011项的乘积 [答]( )
A.3. B.-6. C.. D..
三.解答题(本大题满分78分)本大题共有5题,解答下列各题必须在答题卷的相应编号规定区域内写出必要的步骤.
19.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
如图3所示,已知三棱锥中,点
的中点.
(1)求证四点共面;
(2)已知,点C在球面上,求球M的体积V.
20.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
定义:如果函数,满足
,则称函数是上的“平均值函数”,是它的一个均值点.如上的平均值函数,0就是它的均值点.
(1)判断函数在区间上是否为平均值函数?若是,求出它的均值点;若不是,请说明理由;
(2)若函数上的平均值函数,试确定实数的取值范围.
21.(本题满分16分)本题共有2个小题,第1小题满分7分,第2小题满分9分.
已知是偶函数.
求b的值;
若在函数定义域内总存在区间(m
如图4,某市拟在长为16km的道路OP的一侧修建一条自行车赛道,赛道的前一部分为曲线OSM,该曲线段为函数的图像,且图像的最高点为.赛道的后一段为折线段MNP,为保证参赛队员的安全,限定.
(1)求实数的值以及M、P两点之间的距离;
(2)联结MP,设,试求出用的解析式;
(3)应如何设计,才能使折线段MNP最长?
23.(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分7分,第3小题满分5分.
已知各项都为正数的数列,其中的前n项的和.
(1);
(2)已知p(2)是给定的某个正整数,数列
(),求;
(3)化简.
黄浦区2010学年度第一学期期终基础学业测评
数学试卷(文理合卷)
(2011年1月12日)
参考答案和评分标准
一、填空题
1、;2、;3、 (每空2分) ;
4、;5、; 6、;
7、 ;8、(理科),(文科);9、 ;10、 ;
11、(理科),(文科);12、;
13、(理科)(1)、(3) ,(文科) ; 14、(理科),(文科) 3.
二、选择题: 15、B 16、C 17、D 18、(理科)A(文科)D
三、解答题
19、(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
解(1)
.
.
于是,.
(2)
.
.
.
.
.
20.(本题满分14分) 本题共有2个小题,第1小题满分7分,第2小题满分7分.
解(1)由定义可知,关于x的方程在内有实数根时,
函数.
解,可得.
又,
所以,上的平均值函数,5是它的均值点.
(2)上的平均值函数,
在内有实数根.
,解得.
又
必为均值点,即.
∴所求实数.
21.(本题满分16分)本题共有2个小题,第1小题满分7分,第2小题满分9分.
解(1)由已知可得,,且函数的定义域为D=.
又是偶函数,故定义域D关于原点对称.
于是,b=0().
又对任意
因此所求实数b=0.
(2) 由(1)可知,.
考察函数的图像,可知:
.
因在区间上的函数值组成的集合也是,故必有.
①当时,有,即方程,也就是有两个不相等的正实数根,因此,解得.
②当时,有,化简得,解得.
综上所述,所求实数.
22.(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.
解(1)结合题意和图像,可知,
解此方程组,得,于是.
进一步可得点M的坐标为.
所以,(km).
(2)在,故.
又,
因此,().
(3)把进一步化为:
().
所以,当(km).
可以这样设计:联结MP,分别过点M、P在MP的同一侧作与MP成角的射线,记两射线的交点为N,再修建线段NM和NP,就可得到满足要求的最长折线段MNP赛道.
23.(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分7分,第3小题满分5分.
(理科)解(1),,
.
.
是首项为,公差为2的等差数列;是首项为,公差为2的等差数列.又,可得.
∴.
所以,所求数列的通项公式为.
(2)是给定的正整数(),,
数列是项数为p项的有穷数列.又.
,…
归纳可得.
(3)由(2)可知,进一步可化为:.
所以,
.
(文科)
∴数列是等差比数列,且公差比p=2.
(2)∵数列是等差比数列,且公差比p=2,
,即数列.
.于是,
,
,
…
.
将上述个等式相加,得
.
∴数列的通项公式为.
(3)由(2)可知,
于是,.
所以,数列是等差比数列,且公差比为.
同课章节目录
