16.3 .2分式方程2
文档属性
| 名称 | 16.3 .2分式方程2 |  | |
| 格式 | rar | ||
| 文件大小 | 336.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-01-24 23:07:00 | ||
图片预览




文档简介
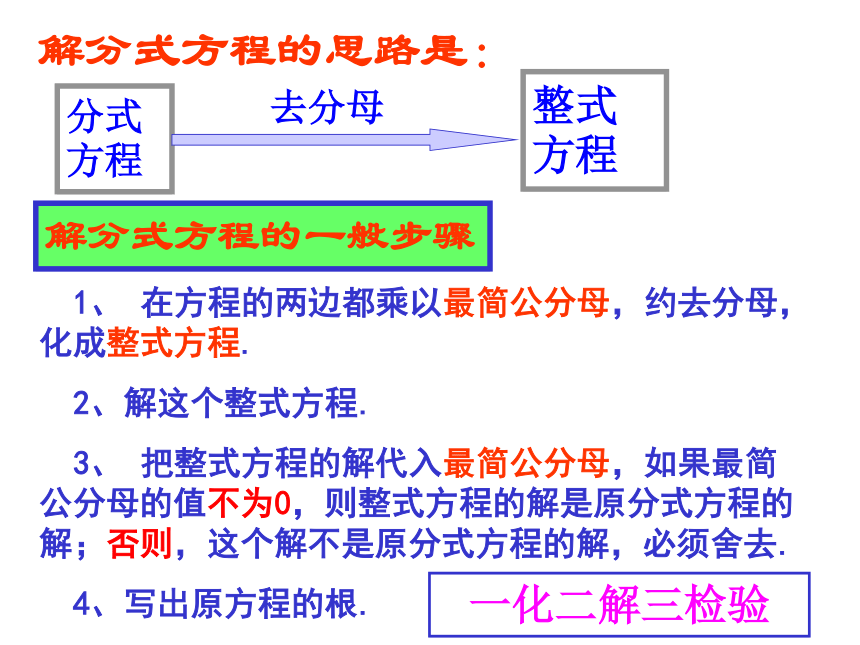
课件10张PPT。16.3 .2 分式方程2 分式方程的定义像这样,分母里含有未知数的方程叫做分式方程。解分式方程的一般步骤 1、 在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2、解这个整式方程.
3、 把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.
4、写出原方程的根.解分式方程的思路是:分式方程整式方程去分母一化二解三检验解方程解:方程两边都乘以 x ( x – 2 ) , 约去分母,得 5 ( x – 2 ) = 7x 解这个整式方程,得 x = – 5 检验:当 x = – 5 时,x ( x – 2 ) = (– 5)(– 5 – 2) = 35 ≠0所以 – 5 是原方程的根.例 1例2.解分式方程在方程的两边都乘以最简公分母 ( x+1)( x – 1 ), 得到整式方程: x + 1 = 2解这个整式方程,得x = 1把 x = 1 代入最简公分母检验:实际上原分式方程无解.( x+1)( x – 1 )=0, 因此x= 1 不是原分式方程的根.解方程解:方程两边都乘以 (x+1) ( x – 1 ) , 约去分母,得 ( x + 1 )2-4 = x2-1 解这个整式方程,得 x = 1 经检验得: x = 1 是增根∴原方程无解.例 3试一试:解分式方程3)解关于x的方程:小练习:作业:1.解关于X的方程 (m≠n,m/n≠0)谢谢!
2、解这个整式方程.
3、 把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.
4、写出原方程的根.解分式方程的思路是:分式方程整式方程去分母一化二解三检验解方程解:方程两边都乘以 x ( x – 2 ) , 约去分母,得 5 ( x – 2 ) = 7x 解这个整式方程,得 x = – 5 检验:当 x = – 5 时,x ( x – 2 ) = (– 5)(– 5 – 2) = 35 ≠0所以 – 5 是原方程的根.例 1例2.解分式方程在方程的两边都乘以最简公分母 ( x+1)( x – 1 ), 得到整式方程: x + 1 = 2解这个整式方程,得x = 1把 x = 1 代入最简公分母检验:实际上原分式方程无解.( x+1)( x – 1 )=0, 因此x= 1 不是原分式方程的根.解方程解:方程两边都乘以 (x+1) ( x – 1 ) , 约去分母,得 ( x + 1 )2-4 = x2-1 解这个整式方程,得 x = 1 经检验得: x = 1 是增根∴原方程无解.例 3试一试:解分式方程3)解关于x的方程:小练习:作业:1.解关于X的方程 (m≠n,m/n≠0)谢谢!
