1.1.2(3) 程序框图的画法
图片预览




文档简介
课件16张PPT。 算法的程序框图最基本的逻辑结构有几种?
算法的程序框图有三种基本的逻辑结构,它
们分别是:顺序结构、条件结构和循环结构. 写出用“二分法”求方程x2-2=0(x>0)的近
似解的算法.
第一步:
第二步: 若f(a)·f(m)<0,则含零点的区
间为[a,m];否则,含零点的区间为[m,b].新
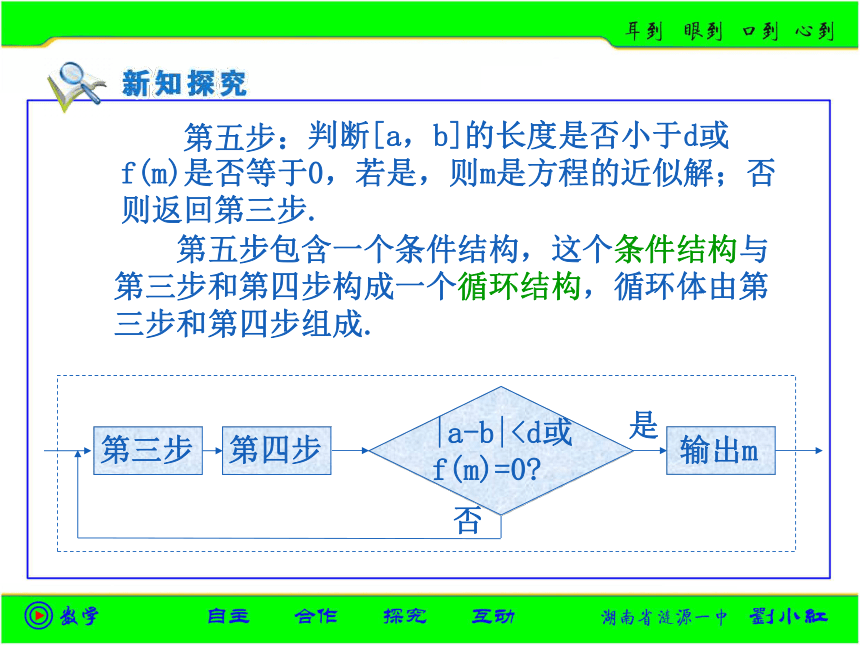
得到的含零点的区间仍记为[a,b]. 判断[a,b]的长度是否小于d或
f(m)是否等于0,若是,则m是方程的近似解;否
则返回第三步. 令f(x)=x2-2,输入精确度d. 确定区间[a,b],满足f(a)·f(b)<0. 第四步:
第五步: 第三步: 写出用“二分法”求方程x2-2=0(x>0)的近
似解的算法.
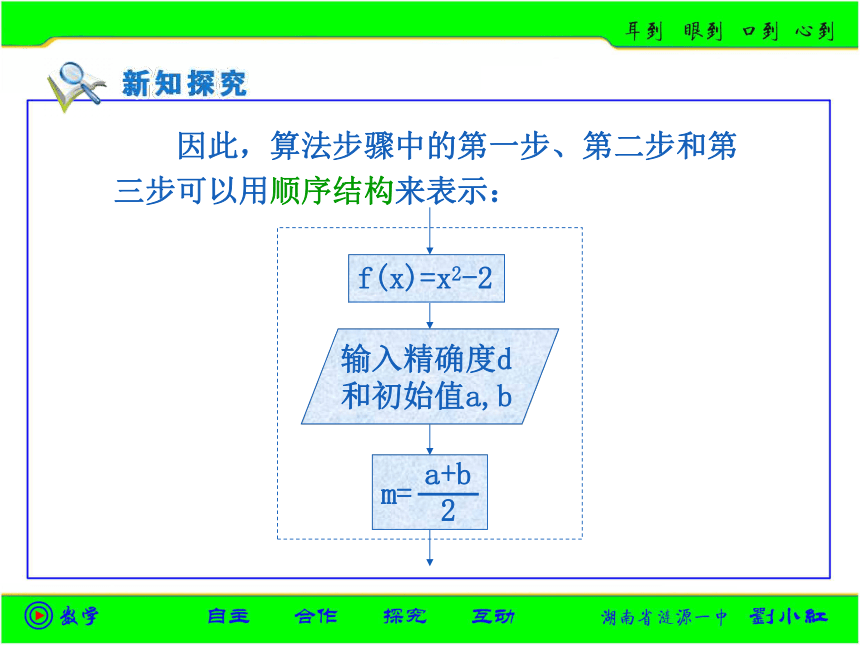
第一步:输入语句用输入框赋值语句用处理框,即: 令f(x)=x2-2,输入精确度d. 确定区间[a,b]. 第二步: 先给出初始区间a,b的值,因此要用输入 框进行输入 第三步: 因此,算法步骤中的第一步、第二步和第
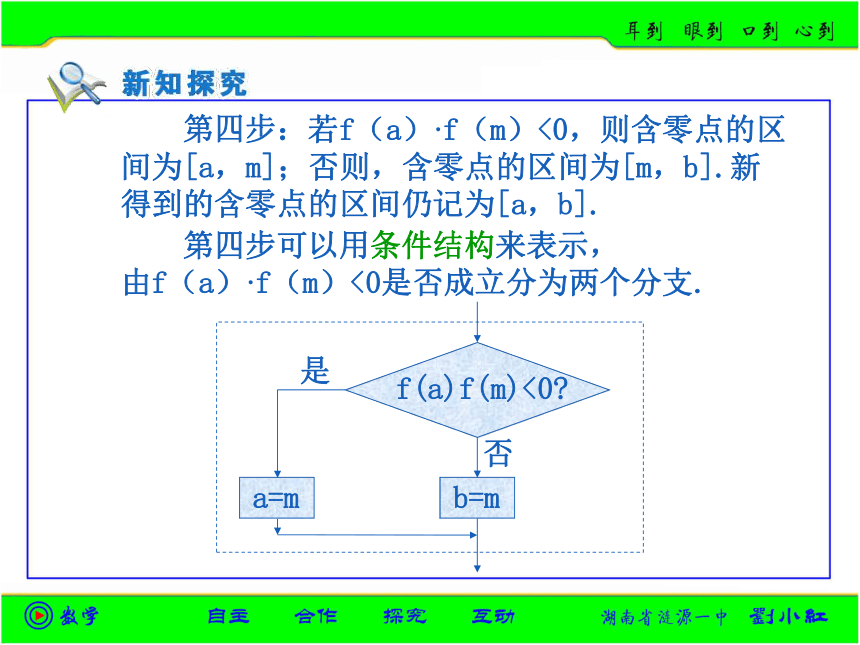
三步可以用顺序结构来表示: 若f(a)·f(m)<0,则含零点的区
间为[a,m];否则,含零点的区间为[m,b].新
得到的含零点的区间仍记为[a,b]. 第四步: 第四步可以用条件结构来表示,
由f(a)·f(m)<0是否成立分为两个分支. 判断[a,b]的长度是否小于d或
f(m)是否等于0,若是,则m是方程的近似解;否
则返回第三步. 第五步: 第五步包含一个条件结构,这个条件结构与
第三步和第四步构成一个循环结构,循环体由第
三步和第四步组成. 将各个步骤连接起来,并画出“开始”与“结
束”两个终端框,得到表示整个算法的程序框图. 某居民区的物业部门每月向居民收取卫生费,计费方法是:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.画出算法的程序框图.第一步:输入人数x,设收取的卫生费为m元.第二步:判断x与3的大小关系.若x>3,则费用为m=5+(x-3)×1.2;若x=3,则费用为m=5.第三步:输出m. 某居民区的物业部门每月向居民收取卫生费,计费方法是:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.画出算法的程序框图.第一步:输入人数x,设收取的卫生费为m元.第二步:判断x与3的大小关系.若x>3,则费用为m=5+(x-3)×1.2;若x=3,则费用为m=5.第三步:输出m. 某居民区的物业部门每月向居民收取卫生费,计费方法是:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.画出算法的程序框图. 某高中男子体育小组的50m跑成绩(单位:s)为:6.4,6.5,7.0,6.8,7.1,7.3,6.9,7.4,7.5. 从这些成绩中搜索出小于6.8s的成绩,画出程序框图. 第一步:把计数变量n的初值设为1. 第二步:输入一个成绩r,判断r与6.8的大小.若
r≥6.8,则执行下一步;若r<6.8,则输
出r,并执行下一步.第三步:使计数变量n的值增加1. 第四步:判断计数变量n与成绩个数9的大小.若
n≤9,则返回第二步;若n>9,则结束. 第一步:把计数变量n的初值设为1. 第二步:输入一个成绩r,判断r与6.8的大小.若
r≥6.8,则执行下一步;若r<6.8,则输
出r,并执行下一步.第三步:使计数变量n的值增加1. 第四步:判断计数变量n与成绩个数9的大小.若
n≤9,则返回第二步;若n>9,则结束. 是否 将各个部分连接起来,加上“开始”和“结束”
两个终端框,这个算法的程序框图如下: 送给“外星人”的“弦图” UFO(不明飞行物)是“外星人”的宇宙飞船吗?是否
存在地球以外生命呢? 这些谜,科学家正在进行探测。倘若有“外星人”存
在,那么,地球上的人类又该如何与他们通话、建立友
谊呢?在“嫦娥奔月”的千年神话变成了现实的今天,科
学家进行了一次又一次的尝试。
送去的图形语言、符号语言、文字语言,无疑是在
作与“外星人”对话的试探。然而,通过收集资料你是否
发现,已给“外星人”送去的图形语言中,还没有数学图
形语言。我国数学家华罗庚认为,如果要与“外星人”交
流信息,不妨把我国古代的“青朱出入图”也送去.
查找并收集“青朱出入图”的相关资料和同学相互交流.
算法的程序框图有三种基本的逻辑结构,它
们分别是:顺序结构、条件结构和循环结构. 写出用“二分法”求方程x2-2=0(x>0)的近
似解的算法.
第一步:
第二步: 若f(a)·f(m)<0,则含零点的区
间为[a,m];否则,含零点的区间为[m,b].新
得到的含零点的区间仍记为[a,b]. 判断[a,b]的长度是否小于d或
f(m)是否等于0,若是,则m是方程的近似解;否
则返回第三步. 令f(x)=x2-2,输入精确度d. 确定区间[a,b],满足f(a)·f(b)<0. 第四步:
第五步: 第三步: 写出用“二分法”求方程x2-2=0(x>0)的近
似解的算法.
第一步:输入语句用输入框赋值语句用处理框,即: 令f(x)=x2-2,输入精确度d. 确定区间[a,b]. 第二步: 先给出初始区间a,b的值,因此要用输入 框进行输入 第三步: 因此,算法步骤中的第一步、第二步和第
三步可以用顺序结构来表示: 若f(a)·f(m)<0,则含零点的区
间为[a,m];否则,含零点的区间为[m,b].新
得到的含零点的区间仍记为[a,b]. 第四步: 第四步可以用条件结构来表示,
由f(a)·f(m)<0是否成立分为两个分支. 判断[a,b]的长度是否小于d或
f(m)是否等于0,若是,则m是方程的近似解;否
则返回第三步. 第五步: 第五步包含一个条件结构,这个条件结构与
第三步和第四步构成一个循环结构,循环体由第
三步和第四步组成. 将各个步骤连接起来,并画出“开始”与“结
束”两个终端框,得到表示整个算法的程序框图. 某居民区的物业部门每月向居民收取卫生费,计费方法是:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.画出算法的程序框图.第一步:输入人数x,设收取的卫生费为m元.第二步:判断x与3的大小关系.若x>3,则费用为m=5+(x-3)×1.2;若x=3,则费用为m=5.第三步:输出m. 某居民区的物业部门每月向居民收取卫生费,计费方法是:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.画出算法的程序框图.第一步:输入人数x,设收取的卫生费为m元.第二步:判断x与3的大小关系.若x>3,则费用为m=5+(x-3)×1.2;若x=3,则费用为m=5.第三步:输出m. 某居民区的物业部门每月向居民收取卫生费,计费方法是:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.画出算法的程序框图. 某高中男子体育小组的50m跑成绩(单位:s)为:6.4,6.5,7.0,6.8,7.1,7.3,6.9,7.4,7.5. 从这些成绩中搜索出小于6.8s的成绩,画出程序框图. 第一步:把计数变量n的初值设为1. 第二步:输入一个成绩r,判断r与6.8的大小.若
r≥6.8,则执行下一步;若r<6.8,则输
出r,并执行下一步.第三步:使计数变量n的值增加1. 第四步:判断计数变量n与成绩个数9的大小.若
n≤9,则返回第二步;若n>9,则结束. 第一步:把计数变量n的初值设为1. 第二步:输入一个成绩r,判断r与6.8的大小.若
r≥6.8,则执行下一步;若r<6.8,则输
出r,并执行下一步.第三步:使计数变量n的值增加1. 第四步:判断计数变量n与成绩个数9的大小.若
n≤9,则返回第二步;若n>9,则结束. 是否 将各个部分连接起来,加上“开始”和“结束”
两个终端框,这个算法的程序框图如下: 送给“外星人”的“弦图” UFO(不明飞行物)是“外星人”的宇宙飞船吗?是否
存在地球以外生命呢? 这些谜,科学家正在进行探测。倘若有“外星人”存
在,那么,地球上的人类又该如何与他们通话、建立友
谊呢?在“嫦娥奔月”的千年神话变成了现实的今天,科
学家进行了一次又一次的尝试。
送去的图形语言、符号语言、文字语言,无疑是在
作与“外星人”对话的试探。然而,通过收集资料你是否
发现,已给“外星人”送去的图形语言中,还没有数学图
形语言。我国数学家华罗庚认为,如果要与“外星人”交
流信息,不妨把我国古代的“青朱出入图”也送去.
查找并收集“青朱出入图”的相关资料和同学相互交流.
