1.3.1（1）算法案例

课件21张PPT。　　在小学我们是怎样求两个正整数的最大公约数的? 用此法求出18与30的公约数.　　8251和6105公有的质因数较大,使用上面的方
法求最大公因数比较困难 ． 辗转相除法：一种古老而有效的算法，这种算法
是欧几里得在公元前300年左右首先提出的，又
叫欧几里得算法.用辗转相除法求8251和6105的最大公因数； 用两数中较大的数除以较小的数，求得商和余数； 8251＝6105×1＋2146 用辗转相除法求8251和6105的最大公因数； 用两数中较大的数除以较小的数，求得商和余数； 8251＝6105×1＋2146 继续重复上面的步骤：6105＝2146×2＋1813 2146＝1813×1＋333 1813＝333×5＋148 333＝148×2＋37 148＝37×4 从右式可知148和37的最大公约数是（　　）.8251与6105的最大公约数也就是37． 37　　所谓辗转相除法,就是对于给定的两个数,
用较大的数除以较小的数.若余数不为零,则将
余数和较小的数构成新的一对数,继续上面的除
法,直到大数被小数除尽,则这时较小的数就是
原来两个数的最大公约数.　　由除法的性质可以知道,对于任意两个正整数，
上述除法步骤总可以在有限步之后完成,从而总可
以用辗转相除法求得两个正整数的最大公约
数． 练习：利用辗转相除法求两数4081与20723的最大
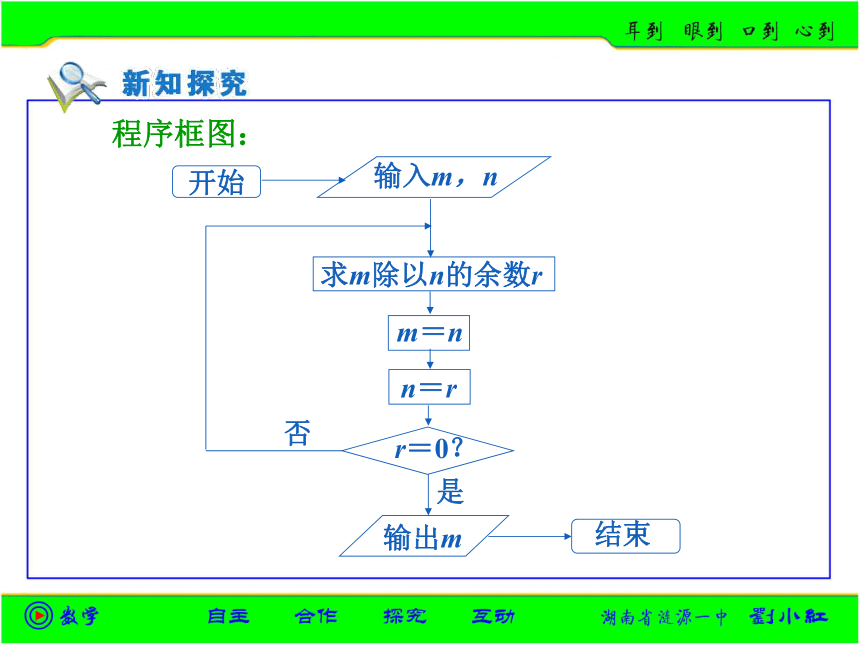
公约数. 答案：53　 　　关键步骤是带余除法,它是一个反复执行、直
到余数等于0才停止的步骤,这实际上是一个循环
结构.思考：你能把辗转相除法编成一个计算机程序吗? 程序框图：程序：　　“更相减损术”是中国古代的数学专著《九
章算术》中的一种算法,它也可以用来求两个数的
最大公约数.　　原文为 “可半者半之，不可半者，副置分母、　
子之数，以少减多，更相减损，求其等也．以等
数约之．”翻译原文：　　第一步，任意给定两个正整数，判断它们是否
都是偶数．若是，用2约简；若不是，执行第二步．　　“更相减损术”是中国古代的数学专著《九
章算术》中的一种算法,它也可以用来求两个数的
最大公约数.　　原文为 “可半者半之，不可半者，副置分母、　
子之数，以少减多，更相减损，求其等也．以等
数约之．”翻译原文：　　第二步，以较大的数减小数，接着把所得的差
与较小的数比较，并以大数减小数．继续这个操作，
直到所得的数相等为止，则这个数（等数）或这个
数与约简的数的乘积就是所求的最大公约数. 例1：用更相减损术求98与63的最大公约数.解：由于63不是偶数，把98和63以大数减小数，
并辗转相减如右式:98－63＝35　63－35＝28 35－28＝7 28－7＝21 21－7＝14 14－7＝7 可见98和63的最大公约数为（　　）.练习：用更相减损术求72和162的最大公因数．　7例1：用更相减损术求98与63的最大公约数.解：由于63不是偶数，把98和63以大数减小数，
并辗转相减如右式:98－63＝35　思考：把更相减损术与辗转相除法比较,你有什么
发现?联系：尽管更相减损术与辗转相除法分别来源于
东西方古代数学名著，但它们都是求最大公约数
的方法且二者的算理也是相似的，有异曲同工之
妙.　 区别：计算上辗转相除法进行的是除法运算，即
辗转相除；更相减损术进行的是减法运算，即辗
转相减，但实质都是一个不断递归的过程，从结
果体现形式来看，辗转相除法体现结果是以相除
余数为0则得到，而更相减损术则以减数与差相等
而得到．思考：你能根据更相减损术设计程序,求两个正整
数的最大公约数吗? 算法分析: 第1步:给定两个正整数m，n，不妨设m＞n ．第2步:若m，n都是偶数，则不断用2约简之，使
它们不同时是偶数，约简后的两个数仍记为m，n
（m＞n）．第3步:求差d＝m－n． 第4步:判断是否有d＝n．若是，则得到d·2k（是
约简整数的2的个数）；否则将n，d中的较大者记
为m，较小者记为n，重复第3步．程序: INPUT“m，n=”，m，n
k=0
WHILE m MOD 2=0 AND n MOD 2=0
m=m/2
n=n/2
k=k+1
WEND
d=m-n
WHILE d≠n
IF d>n THEN
m=d
END IF
IF d m=n
n=d
END IF
d=m-n
WEND
d=d*2^k
PRINT d
END程序框图： 否练习: