3.1.1随机事件的概率
图片预览







文档简介
课件22张PPT。 客观世界中,有些事物的发生是偶然的,有些事物的发生是必然的,而且偶然与必然之间往往有某种内在联系.例如:某种水稻种子发芽后,在一定条件(温度、水分、土壤、阳光)下,一定会经历分蘖、生长、颖花、结穗、成熟等过程,这个生长规律是确定的;但是在这个过程中,每一粒发芽种子的分蘖数是多少,接穗率是多少,茎秆高是多少,接穗实粒是多少,粒重有是多少,这些却都是不确定的. 农业生产实践告诉我们,在一定的条件S(温
度、水分、土壤、阳光)下,发芽种子一定会分蘖.像这种在一定的条件S(温度、水分、土壤、
阳光)下,必然会发生的事件(发芽种子分蘖)称
为必然事件.另一方面,“发芽种子不分蘖”这一
事件一定不会发生,像这种在条件S下一定不会
发生的事件称为不可能事件.另外一定的条件S
(温度、水分、土壤、阳光)下,一粒发芽种子会
分对少蘖又是不确定的,像这种在条件S下,不
能事先预测结果的事件称为随机事件. 随机事件:在条件S下可能发生也可能不发生的事件,叫做相对于条件S的随机事件,简称随机事件.相关概念
必然事件:在条件S下一定会发生的事件,叫做相
对于条件S的必然事件,简称必然事件.
不可能事件:在条件S下一定不会发生的事件,叫
做相对于条件S的不可能事件,简称不可能事件.
确定事件:必然事件与不可能事件统称为相对于条件S的确定事件,简称确定事件.
确定事件和随机事件统称为事件,一般用大写字母A、B、C……表示. 观察下列事件发生与否,判断它们属于哪种
事件.
(1)地球不停地转动;????????
(2)木柴燃烧,产生能量;????
(3)在常温下,石头风化;????
(4)某人射击一次,中靶;
(5)掷一枚硬币,出现正面;??
(6)在标准大气压下且温度低
于0℃时,雪融化. 思考:你还能举出一些现实生活中的随机事件、
必然事件、不可能事件的实例吗? 必然事件 必然事件 不可能事件 不可能事件 随机事件 随机事件 实验:把一枚硬币抛多次,观察其出现的结果,
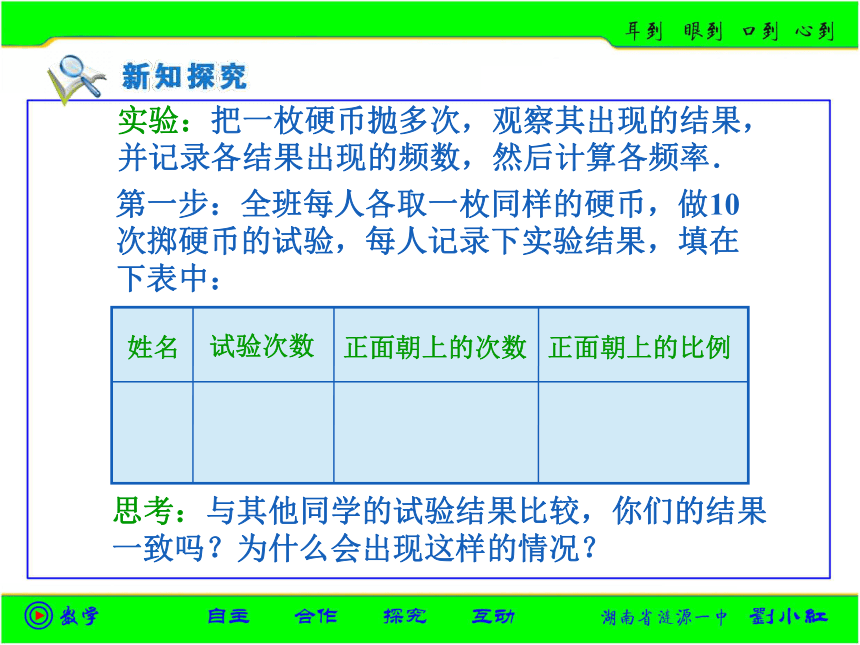
并记录各结果出现的频数,然后计算各频率.思考:与其他同学的试验结果比较,你们的结果
一致吗?为什么会出现这样的情况? 第一步:全班每人各取一枚同样的硬币,做10
次掷硬币的试验,每人记录下实验结果,填在
下表中:实验:把一枚硬币抛多次,观察其出现的结果,
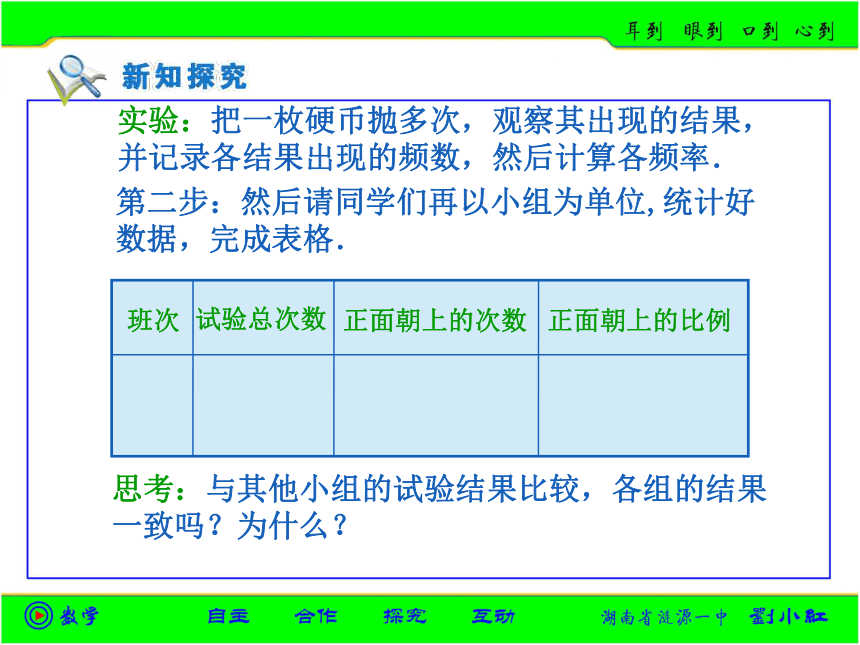
并记录各结果出现的频数,然后计算各频率.思考:与其他小组的试验结果比较,各组的结果
一致吗?为什么? 第二步:然后请同学们再以小组为单位,统计好
数据,完成表格.实验:把一枚硬币抛多次,观察其出现的结果,
并记录各结果出现的频数,然后计算各频率.第三步:请一个同学把全班同学的试验结果统计
一下,填入下表:实验:把一枚硬币抛多次,观察其出现的结果,
并记录各结果出现的频数,然后计算各频率.第四步:请把全班每个同学的实验中正面朝上
的次数收集起来,用横轴为实验结果,仅取两
个值:1(正面)和0(反面),纵轴为实验结
果出现的比例,画出条形图.思考:这个条形图有什么特点? 实验:把一枚硬币抛多次,观察其出现的结果,
并记录各结果出现的频数,然后计算各频率.第五步:请同学们找出掷硬币时“正面朝上“这个
事件发生的规律性.结论分析:
实验(1)中只出现两种结果,没有其它结果,
每一次试验的结果不固定,但只是“正面”、“反
面”两种中的一种,且它们出现的比例均接近于
0.5,但不相等.探究:如果同学们重复一次上面的实验,全班的
汇总结果还会和这次的汇总结果一致吗?如果不
一致,你能说出原因吗? 思考:频率的取值范围是什么?分析:因为0≤nA≤n,所以频率的取值范围是
[0,1].必然事件出现的频率为1,不可能事件
出现的频率为0. 我们会发现,当试验次数很多时,出现正面的频率值正在0.5附近摆动.一般来说随机事件A在每次
试验中是否发生是不能预知的,但是在大量重复实验后,随着次数的增加,事件A发生的频率会逐渐稳定
在区间[0,1]中的某个常数上. 探究:如果允许你做大量重复试验,你认为结果又如何呢? 历史上一些抛掷硬币试验结果表:概率的定义:
对于给定的随机事件A,如果随着实验次数
的增加,事件A发生的频率fn(A)稳定在某个常数上,把这个常数记作P(A),称为事件A的概率. 必然事件的概率为1,不可能事件的概率为
0,随机事件的概率为0≤P(A)≤1 .知道事件概率的必要性
概率是用来度量随机事件发生可能性大小的
量,知道事件的概率可以为我们决策提供依据.思考:事件A发生的频率fn(A)是不是不变的?事
件A的概率P(A)是不是不变的?它们之间有什么
区别与联系?分析:
(1)频率是概率的近似值,随着试验次数的增
加,频率会越来越接近概率.
(2)频率本身是随机的,在试验前不能确定.
做同样次数的重复试验得到事件的频率会不同.
(3)概率是频率的稳定值,概率是一个确定的
数,是客观存在的,与每次试验无关.随机事件 必然事件 不可能事件 随机事件 例1、一个地区从某年起几年之内的新生婴儿数及其中的男婴数如下: (1)填写上表中的男婴出生频率(如果用计算器计算,
结果保留到小数点后第3位); 解:(1)上表中的男婴出生的频率依次为例1、一个地区从某年起几年之内的新生婴儿数及其中的男婴数如下: 5544 9607 13520 17190 2883 4970 6994 8892 (2)这一地区男婴出生的概率约是多少?解:(2)由(1)知,某年起几年之内新生婴儿中男婴出
生的频率虽然不尽相同,但频率总是在0.517的附近摆动,
可知该地区新生婴儿中男婴出生的概率约是0.517 . 练习1: 某种新药在使用的患者中进行调查的结果如下表: 请填写表中有效频率一栏,并指出该药的
有效概率是多少?(88%) 0.85 0.90 0.87 0.884 0.88 练习2: 做试验,掷一个骰子100次,填下表: 练习3: (1)给出一个概率很小的随机事件的例子; (2)给出一个概率很大的随机事件的例子.
度、水分、土壤、阳光)下,发芽种子一定会分蘖.像这种在一定的条件S(温度、水分、土壤、
阳光)下,必然会发生的事件(发芽种子分蘖)称
为必然事件.另一方面,“发芽种子不分蘖”这一
事件一定不会发生,像这种在条件S下一定不会
发生的事件称为不可能事件.另外一定的条件S
(温度、水分、土壤、阳光)下,一粒发芽种子会
分对少蘖又是不确定的,像这种在条件S下,不
能事先预测结果的事件称为随机事件. 随机事件:在条件S下可能发生也可能不发生的事件,叫做相对于条件S的随机事件,简称随机事件.相关概念
必然事件:在条件S下一定会发生的事件,叫做相
对于条件S的必然事件,简称必然事件.
不可能事件:在条件S下一定不会发生的事件,叫
做相对于条件S的不可能事件,简称不可能事件.
确定事件:必然事件与不可能事件统称为相对于条件S的确定事件,简称确定事件.
确定事件和随机事件统称为事件,一般用大写字母A、B、C……表示. 观察下列事件发生与否,判断它们属于哪种
事件.
(1)地球不停地转动;????????
(2)木柴燃烧,产生能量;????
(3)在常温下,石头风化;????
(4)某人射击一次,中靶;
(5)掷一枚硬币,出现正面;??
(6)在标准大气压下且温度低
于0℃时,雪融化. 思考:你还能举出一些现实生活中的随机事件、
必然事件、不可能事件的实例吗? 必然事件 必然事件 不可能事件 不可能事件 随机事件 随机事件 实验:把一枚硬币抛多次,观察其出现的结果,
并记录各结果出现的频数,然后计算各频率.思考:与其他同学的试验结果比较,你们的结果
一致吗?为什么会出现这样的情况? 第一步:全班每人各取一枚同样的硬币,做10
次掷硬币的试验,每人记录下实验结果,填在
下表中:实验:把一枚硬币抛多次,观察其出现的结果,
并记录各结果出现的频数,然后计算各频率.思考:与其他小组的试验结果比较,各组的结果
一致吗?为什么? 第二步:然后请同学们再以小组为单位,统计好
数据,完成表格.实验:把一枚硬币抛多次,观察其出现的结果,
并记录各结果出现的频数,然后计算各频率.第三步:请一个同学把全班同学的试验结果统计
一下,填入下表:实验:把一枚硬币抛多次,观察其出现的结果,
并记录各结果出现的频数,然后计算各频率.第四步:请把全班每个同学的实验中正面朝上
的次数收集起来,用横轴为实验结果,仅取两
个值:1(正面)和0(反面),纵轴为实验结
果出现的比例,画出条形图.思考:这个条形图有什么特点? 实验:把一枚硬币抛多次,观察其出现的结果,
并记录各结果出现的频数,然后计算各频率.第五步:请同学们找出掷硬币时“正面朝上“这个
事件发生的规律性.结论分析:
实验(1)中只出现两种结果,没有其它结果,
每一次试验的结果不固定,但只是“正面”、“反
面”两种中的一种,且它们出现的比例均接近于
0.5,但不相等.探究:如果同学们重复一次上面的实验,全班的
汇总结果还会和这次的汇总结果一致吗?如果不
一致,你能说出原因吗? 思考:频率的取值范围是什么?分析:因为0≤nA≤n,所以频率的取值范围是
[0,1].必然事件出现的频率为1,不可能事件
出现的频率为0. 我们会发现,当试验次数很多时,出现正面的频率值正在0.5附近摆动.一般来说随机事件A在每次
试验中是否发生是不能预知的,但是在大量重复实验后,随着次数的增加,事件A发生的频率会逐渐稳定
在区间[0,1]中的某个常数上. 探究:如果允许你做大量重复试验,你认为结果又如何呢? 历史上一些抛掷硬币试验结果表:概率的定义:
对于给定的随机事件A,如果随着实验次数
的增加,事件A发生的频率fn(A)稳定在某个常数上,把这个常数记作P(A),称为事件A的概率. 必然事件的概率为1,不可能事件的概率为
0,随机事件的概率为0≤P(A)≤1 .知道事件概率的必要性
概率是用来度量随机事件发生可能性大小的
量,知道事件的概率可以为我们决策提供依据.思考:事件A发生的频率fn(A)是不是不变的?事
件A的概率P(A)是不是不变的?它们之间有什么
区别与联系?分析:
(1)频率是概率的近似值,随着试验次数的增
加,频率会越来越接近概率.
(2)频率本身是随机的,在试验前不能确定.
做同样次数的重复试验得到事件的频率会不同.
(3)概率是频率的稳定值,概率是一个确定的
数,是客观存在的,与每次试验无关.随机事件 必然事件 不可能事件 随机事件 例1、一个地区从某年起几年之内的新生婴儿数及其中的男婴数如下: (1)填写上表中的男婴出生频率(如果用计算器计算,
结果保留到小数点后第3位); 解:(1)上表中的男婴出生的频率依次为例1、一个地区从某年起几年之内的新生婴儿数及其中的男婴数如下: 5544 9607 13520 17190 2883 4970 6994 8892 (2)这一地区男婴出生的概率约是多少?解:(2)由(1)知,某年起几年之内新生婴儿中男婴出
生的频率虽然不尽相同,但频率总是在0.517的附近摆动,
可知该地区新生婴儿中男婴出生的概率约是0.517 . 练习1: 某种新药在使用的患者中进行调查的结果如下表: 请填写表中有效频率一栏,并指出该药的
有效概率是多少?(88%) 0.85 0.90 0.87 0.884 0.88 练习2: 做试验,掷一个骰子100次,填下表: 练习3: (1)给出一个概率很小的随机事件的例子; (2)给出一个概率很大的随机事件的例子.
