1.1.1任意角

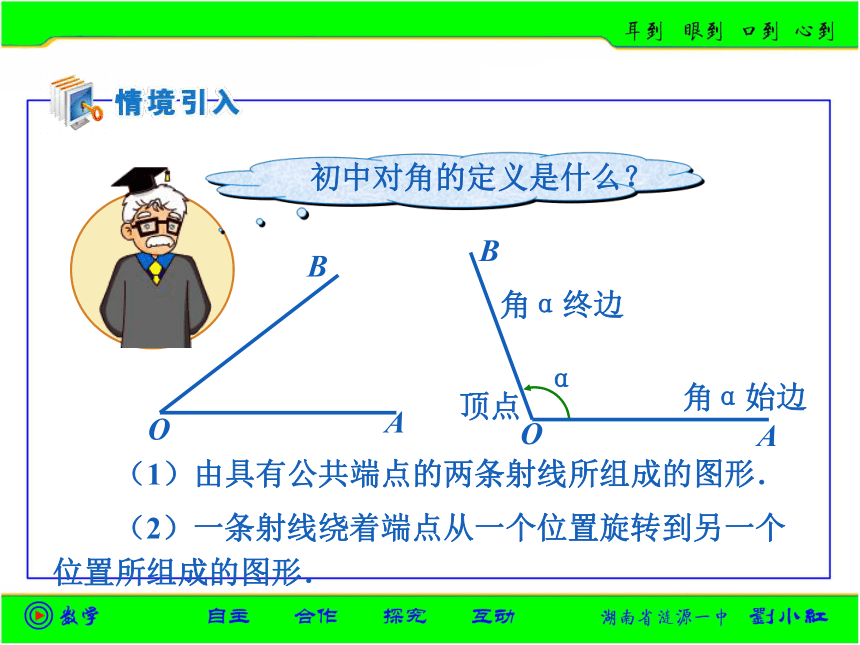
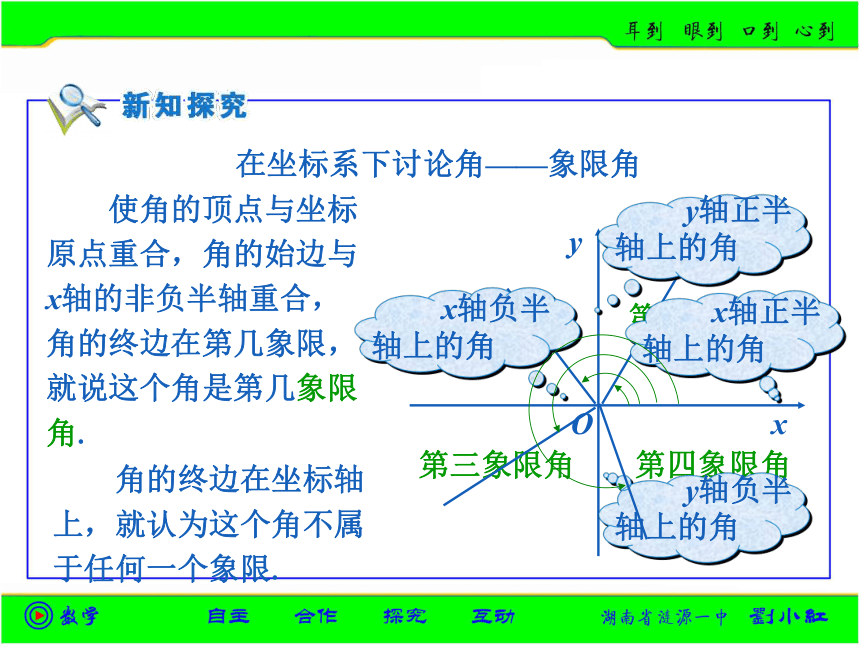
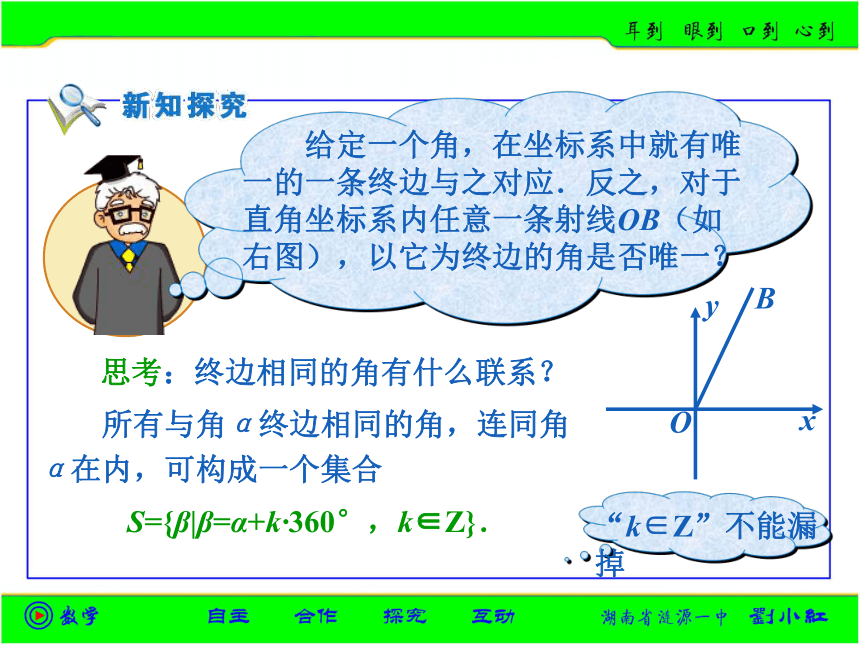
课件16张PPT。O角α终边角α始边Oα　　（1）由具有公共端点的两条射线所组成的图形．　　（2）一条射线绕着端点从一个位置旋转到另一个位置所组成的图形．顶点0°~360°（即0°≤α＜360°）和周角．　　跳水中有“转体720°”（转体2周）、体操中有“转体1080°”（转体3周）等这样的动作名称．而旋转的方向也有顺时针和逆时针的不同，右下角两个齿轮的旋转方向相反，那么他们旋转所成的角也有不同的方向．　　如果一条射线绕它的端点按逆时针方向旋转形成的角叫做正角(positive angle)；Bα正角负角Bβ　　按顺时针方向旋转形成的角叫做负角(negative angle)；　　没有作任何旋转形成了一个零角(zero angle)．零角的始边与终边重合，如果α是零角，那么α=0°．零角(B)α= 0°第一象限角第二象限角第三象限角第四象限角在坐标系下讨论角——象限角　　使角的顶点与坐标原点重合，角的始边与x轴的非负半轴重合，角的终边在第几象限，就说这个角是第几象限角.　　角的终边在坐标轴上，就认为这个角不属于任何一个象限.思考：终边相同的角有什么联系？　　所有与角α终边相同的角，连同角α在内，可构成一个集合S={β|β=α+k·360°，k∈Z}．　　例1：在0°~360°范围内，找出与-950°12'角终边相同的角，并判定它是第几象限的角.解： -950°12' =129°48' -3×360°，　　所以在0°~360°范围内，与-950°12' 角终边相同的角是129°48' ，它是第二象限的角.例2：写出终边在y轴上的角的集合.　　解：在0°~360°范围内，终边在y轴上的角有两个，即90°和270°．　　因此，所有与90°角终边相同的角构成的集合　　而所有与270°角终边相同的角构成的集合S1={β|β=90°+k·360°，k∈Z}，S2={β|β=270°+k·360°，k∈Z}．　　于是，终边在y轴上的角的集合S=S1∪S2={β|β=90°+2k·180°，k∈Z} ∪{β|β=90°+(2k+1)180°，k∈Z}={β|β=90°+n·180°，n∈Z}．　　例3：写出终边在直线y=x上的角的集合S，并把S中适合不等式-360°≤β＜720°的元素β写出来.　　解：在0°~360°范围内，终边在直线y=x上的角有两个，即45°，225°．S中适合-360°≤β＜720°的元素是：　　　因此终边在直线 y = x 上的角的集合S={β|β=45°+k·360°，k∈Z}　　　　　={β|β=45°+k·180°，k∈Z}．∪{β|β=225°+k·360°，k∈Z}45°+2×180°=405°；　45°+3×180°=585°．45°-2×180°=-315°；　 45°-1×180°=-135°；45°+0×180°=45°；　45°+1×180°=225°；　　1．闹钟的分针在旋转时所形成的角是______角（填“正”、“负”）；如果闹钟快了1.25小时，则只需将分针旋转_____________度（只要填一个具体的数）可以将它校准．　　2．今天是星期三，那么7k（k∈Z）天后的那一天是星期______，100天后那一天是星期________.负450或3870五三　　3.写出与下列各角终边相同的角的集合，并把集合中适合不等式-720°≤β＜360°的元素β写出来：（1）1303°18′； （2）-225°．解：（1）{β|β＝1303°18′+k·360°，k∈Z}适合不等式-720°≤β＜360°的元素β有：-496°42′，-136°42′，223°18′.（2）{β|β＝-225°+k·360°，k∈Z}适合不等式-720°≤β＜360°的元素β有：-585°，-225°，135°.　　1．比一比下列四个集合的范围：Ａ＝｛锐角｝，
B＝｛0°~90°的角｝，C＝｛小于90°的角｝，
D＝｛第一象限角｝．解：
A＝｛锐角｝={θ|0°＜θ＜90°}
B＝｛0°~90°的角｝={θ|0°≤θ<90°}
C＝｛小于90°的角｝={θ|θ＜90°}
D＝｛第一象限角｝
=｛θ｜k·360°＜θ＜90°＋k·360°，k∈Z}答：α＋β=k· 360°，k∈Z．