1.1.2弧度制
图片预览




文档简介
(共19张PPT)
度量长度的单位有哪些?
米
尺
码
度量重量的单位有哪些?
千克
斤
磅
角的度量单位是什么?
度,且1度等于周角的
360
1
还有度量角的单位吗?
1°=60′=3600″
弧度制:
把等于半径长的圆弧所对的圆心角叫做1弧度(radian)的角.用符号rad表示,读作弧度.
当圆的半径增大时,圆心角会增大吗?
不会,增大半径只会使圆面积增大;
而角的大小只与弧长与半径的比值的大小有关.
360°
180°
0
-π
-2
2r
1
r
逆时针方向
2πr
逆时针方向
πr
∠AOB的度数
∠AOB的弧度数
OB旋转的方向
AB的长
⌒
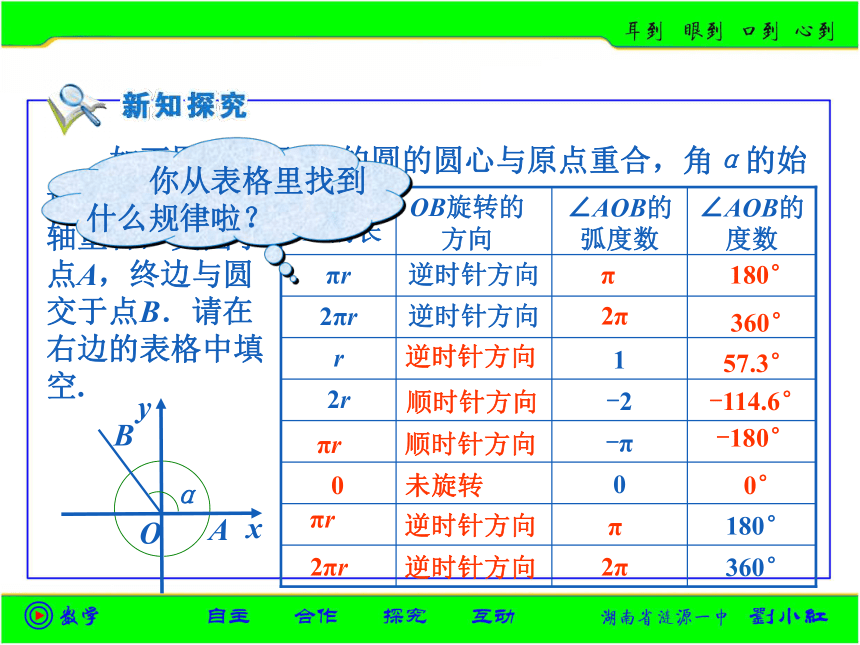
如下图,半径为r的圆的圆心与原点重合,角α的始边与x轴的正半
轴重合,交圆于点A,终边与圆交于点B.请在右边的表格中填空.
x
O
y
α
A
B
逆时针方向
逆时针方向
逆时针方向
顺时针方向
顺时针方向
未旋转
πr
2πr
πr
0
2π
π
π
2π
180°
360°
57.3°
-114.6°
-180°
0°
你从表格里找到什么规律啦?
1.一般地,正角的弧度数是一个______数; 负角的弧度数是一个______数;零角的弧度数是_____.
正
负
0
2.如果半径为r的圆的圆心角α所对的弧长为l,那么,角α的弧度数的绝对值是|α|=________
l
r
3.角度制与弧度制的换算公式:
180°=π rad
1°= rad≈0.01745rad
π
180
1 rad=( )°≈57.30°=57°18′
180
π
例1:按照下列要求,把67°30′化成弧度:
(2)利用计算器有
MODE
2
67
。 , ,,
30
SHIFT
DRG
1
=
1.178097425.
因此, 67°30′≈1.178 rad.
(1)精确值;
(2)精确到0.001的近似值.
解:(1)因为67°30′=( )°,
135
2
所以67°30′= rad× = πrad
π
180
135
2
3
8
MODE
。 , ,,
例2:将3.14 rad换算成角度(用角度表示,精确
到0.001).
解:利用计算器
MODE
MODE
1
3.14
SHIFT
DRG
2
=
179.9087477.
因此,3.14 rad≈179.909°.
1.今后用弧度制表示角时,“弧度”二字或“rad”通常省略不写,而只写该角所对应的弧度数.
如角α=2,表示α是2 rad的角.
2.角度制与弧度制可以自由互换,但在同一个代数式中不能同时使用两种制度:
×
注意
sin 就表示 rad的角的正弦,即
π
3
π
3
π
3
sin =sin60°=
√3
2
如30°+
π
4
1.填写下列特殊角的度数与弧度数的对应表:
60°
90°
180°
270°
-240 °
-108°
-15°
弧度
360°
150°
135°
120°
45°
30°
0°
度
π
2
π
3
π
3π
2
2π
5π
6
3π
4
2π
3
π
4
π
6
0
π
8
-
π
15
-
-3π
7π
4
-
弧度
-540°
-315°
-22.5°
-12°
度
4π
3
-
3π
5
-
π
12
-
角的集合与实数集之间的一一对应关系:
正角
零角
负角
正实数
零
负实数
实数集R
任意角的集合
2.用弧度制表示终边在坐标轴上的角的集合
__________________________________________.
解:终边在x轴上的角的集合是
终边在y轴上的角的集合是
所以,终边在坐标轴上的角的集合是
S1={β|β=kπ,k∈Z}.
S2={β|β=kπ+ ,k∈Z}.
π
2
S={β|β= ,k∈Z}.
kπ
2
例3:利用弧度证明下面关于扇形的公式:
S= lR= αR2.
1
2
1
2
其中R是半径,l是弧长,α(0<α<2π)为圆心角,S为扇形面积.
证明:由公式|α|= 可得:
l
r
l=αR.
α
O
R
l
l=
nπR
180
由于半径为R ,圆心角为n°的扇形的弧长公式和面积公式分别是
S=
nπR2
360
将n°转化为弧度,得:
α=
nπ
180
于是:
1
2
S= αR2
将l=αR代入上式,可得:
1
2
S= lR
S= lR= αR2.
1
2
1
2
所以关于扇形的公式有:
α
O
R
l
3.已知扇形周长为10cm,面积为6cm2,求扇形中心角的弧度数.
∴
或
∴
解:设扇形中心角的弧度数为α(0<α<2π),弧长为l,半径为r,由题意:
l+2r =10
l · r =6
1
2
r2-5r+6=0
r =2
l =6
r =3
l =4
α= =3或
r
l
4
3
α
O
r
l
例4:CCTV每晚的新闻联播从开始到结束,时针与分针分别走了多少弧度?当新闻联播结束时,时针与分针此时所夹的劣弧所对的圆心角的弧度数是多少?
因此,在30分钟内时针走的弧度是 ,分针走的弧度是π.当新闻联播结束时,时针与分针此时所夹的劣弧所对的圆心角的弧度数是 .
π
12
π
6
π
12
+ =
π
4
解: CCTV每晚的新闻联播是从7点开始播到7点半,一共30分钟.由于钟面被平均分成12大格,所以时针或分针每走一大格所对应的弧度是 .
2π
12
中央1台每天的焦点访谈在每晚7点多播出,播出时时针与分针重合,你知道焦点访谈何时播出吗?
解:7点时,时针指向7,分针指向12,此时时针与分针的夹角为 ,当分针走到与时针重合时,分针要比时针多走 .设焦点访谈在7点t分播出,则有
7π
6
7π
6
2πt
60
= ÷12+
2πt
60
7π
6
解得 t≈38
答:焦点访谈大约在7点38分播出.
度量长度的单位有哪些?
米
尺
码
度量重量的单位有哪些?
千克
斤
磅
角的度量单位是什么?
度,且1度等于周角的
360
1
还有度量角的单位吗?
1°=60′=3600″
弧度制:
把等于半径长的圆弧所对的圆心角叫做1弧度(radian)的角.用符号rad表示,读作弧度.
当圆的半径增大时,圆心角会增大吗?
不会,增大半径只会使圆面积增大;
而角的大小只与弧长与半径的比值的大小有关.
360°
180°
0
-π
-2
2r
1
r
逆时针方向
2πr
逆时针方向
πr
∠AOB的度数
∠AOB的弧度数
OB旋转的方向
AB的长
⌒
如下图,半径为r的圆的圆心与原点重合,角α的始边与x轴的正半
轴重合,交圆于点A,终边与圆交于点B.请在右边的表格中填空.
x
O
y
α
A
B
逆时针方向
逆时针方向
逆时针方向
顺时针方向
顺时针方向
未旋转
πr
2πr
πr
0
2π
π
π
2π
180°
360°
57.3°
-114.6°
-180°
0°
你从表格里找到什么规律啦?
1.一般地,正角的弧度数是一个______数; 负角的弧度数是一个______数;零角的弧度数是_____.
正
负
0
2.如果半径为r的圆的圆心角α所对的弧长为l,那么,角α的弧度数的绝对值是|α|=________
l
r
3.角度制与弧度制的换算公式:
180°=π rad
1°= rad≈0.01745rad
π
180
1 rad=( )°≈57.30°=57°18′
180
π
例1:按照下列要求,把67°30′化成弧度:
(2)利用计算器有
MODE
2
67
。 , ,,
30
SHIFT
DRG
1
=
1.178097425.
因此, 67°30′≈1.178 rad.
(1)精确值;
(2)精确到0.001的近似值.
解:(1)因为67°30′=( )°,
135
2
所以67°30′= rad× = πrad
π
180
135
2
3
8
MODE
。 , ,,
例2:将3.14 rad换算成角度(用角度表示,精确
到0.001).
解:利用计算器
MODE
MODE
1
3.14
SHIFT
DRG
2
=
179.9087477.
因此,3.14 rad≈179.909°.
1.今后用弧度制表示角时,“弧度”二字或“rad”通常省略不写,而只写该角所对应的弧度数.
如角α=2,表示α是2 rad的角.
2.角度制与弧度制可以自由互换,但在同一个代数式中不能同时使用两种制度:
×
注意
sin 就表示 rad的角的正弦,即
π
3
π
3
π
3
sin =sin60°=
√3
2
如30°+
π
4
1.填写下列特殊角的度数与弧度数的对应表:
60°
90°
180°
270°
-240 °
-108°
-15°
弧度
360°
150°
135°
120°
45°
30°
0°
度
π
2
π
3
π
3π
2
2π
5π
6
3π
4
2π
3
π
4
π
6
0
π
8
-
π
15
-
-3π
7π
4
-
弧度
-540°
-315°
-22.5°
-12°
度
4π
3
-
3π
5
-
π
12
-
角的集合与实数集之间的一一对应关系:
正角
零角
负角
正实数
零
负实数
实数集R
任意角的集合
2.用弧度制表示终边在坐标轴上的角的集合
__________________________________________.
解:终边在x轴上的角的集合是
终边在y轴上的角的集合是
所以,终边在坐标轴上的角的集合是
S1={β|β=kπ,k∈Z}.
S2={β|β=kπ+ ,k∈Z}.
π
2
S={β|β= ,k∈Z}.
kπ
2
例3:利用弧度证明下面关于扇形的公式:
S= lR= αR2.
1
2
1
2
其中R是半径,l是弧长,α(0<α<2π)为圆心角,S为扇形面积.
证明:由公式|α|= 可得:
l
r
l=αR.
α
O
R
l
l=
nπR
180
由于半径为R ,圆心角为n°的扇形的弧长公式和面积公式分别是
S=
nπR2
360
将n°转化为弧度,得:
α=
nπ
180
于是:
1
2
S= αR2
将l=αR代入上式,可得:
1
2
S= lR
S= lR= αR2.
1
2
1
2
所以关于扇形的公式有:
α
O
R
l
3.已知扇形周长为10cm,面积为6cm2,求扇形中心角的弧度数.
∴
或
∴
解:设扇形中心角的弧度数为α(0<α<2π),弧长为l,半径为r,由题意:
l+2r =10
l · r =6
1
2
r2-5r+6=0
r =2
l =6
r =3
l =4
α= =3或
r
l
4
3
α
O
r
l
例4:CCTV每晚的新闻联播从开始到结束,时针与分针分别走了多少弧度?当新闻联播结束时,时针与分针此时所夹的劣弧所对的圆心角的弧度数是多少?
因此,在30分钟内时针走的弧度是 ,分针走的弧度是π.当新闻联播结束时,时针与分针此时所夹的劣弧所对的圆心角的弧度数是 .
π
12
π
6
π
12
+ =
π
4
解: CCTV每晚的新闻联播是从7点开始播到7点半,一共30分钟.由于钟面被平均分成12大格,所以时针或分针每走一大格所对应的弧度是 .
2π
12
中央1台每天的焦点访谈在每晚7点多播出,播出时时针与分针重合,你知道焦点访谈何时播出吗?
解:7点时,时针指向7,分针指向12,此时时针与分针的夹角为 ,当分针走到与时针重合时,分针要比时针多走 .设焦点访谈在7点t分播出,则有
7π
6
7π
6
2πt
60
= ÷12+
2πt
60
7π
6
解得 t≈38
答:焦点访谈大约在7点38分播出.
