1.2.1(1)任意角的三角函数(一)
文档属性
| 名称 | 1.2.1(1)任意角的三角函数(一) |

|
|
| 格式 | rar | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-01-24 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
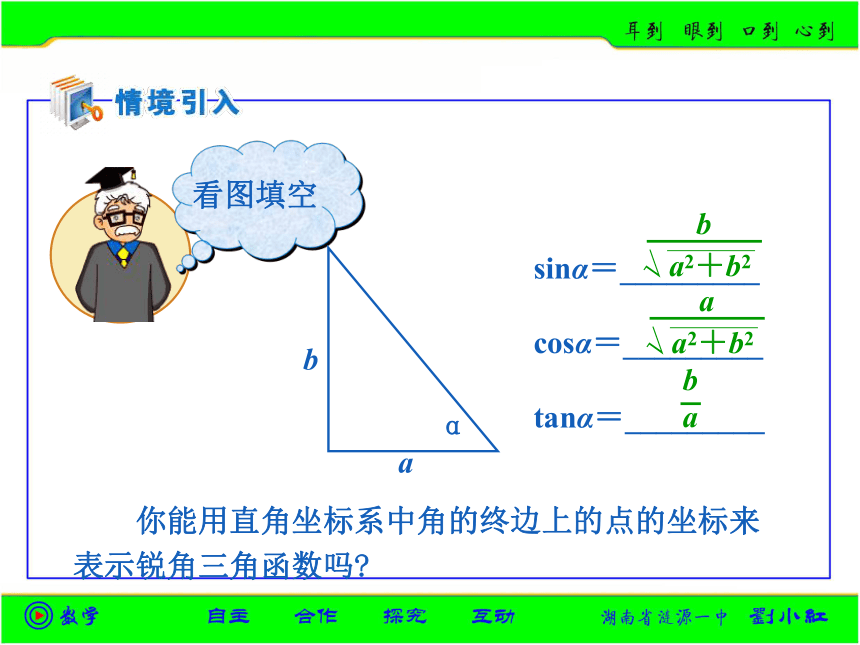
看图填空
你能用直角坐标系中角的终边上的点的坐标来表示锐角三角函数吗
α
b
a
sinα=_________
cosα=_________
tanα=_________
a2+b2
√
b
a2+b2
√
a
ba
想一想:对于确定的α,这三个比值会随P点在α的终边上的位置的改变而比值改变吗?
b
r
a
r
b
a
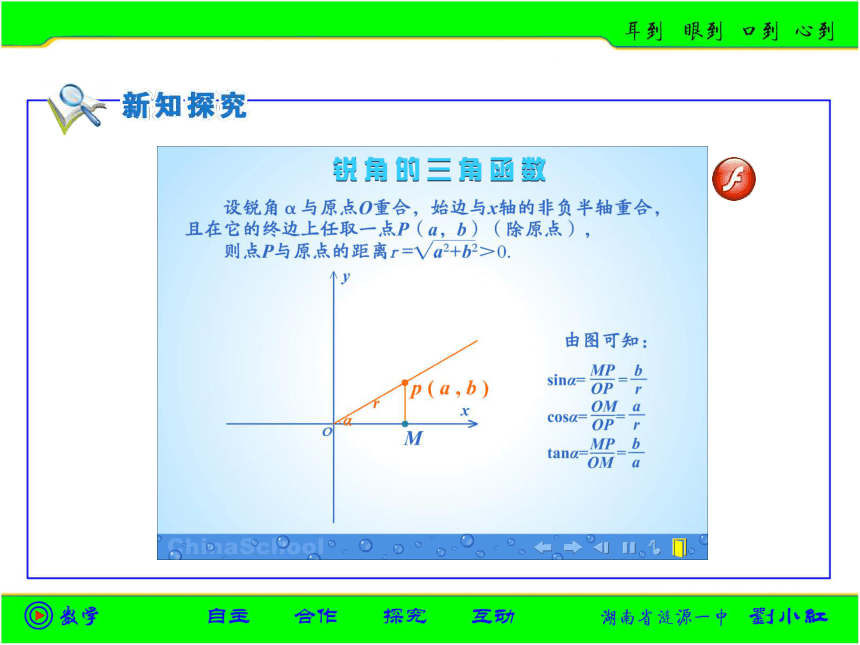
x
O
y
M
P(a,b)
α
r
sinα=________;
cosα=________;
tanα=________.
√
设锐角α与原点O重合,始边与x轴的非负半轴重合,且在它的终边上任取一点P(a,b)(除原点),则点P与原点的距离r = a2+b2>0.
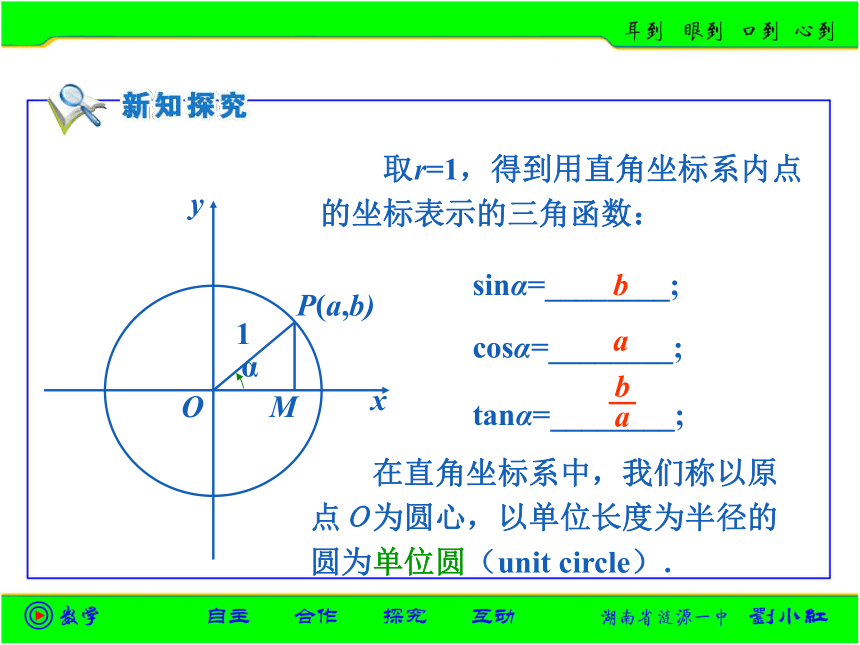
取r=1,得到用直角坐标系内点的坐标表示的三角函数:
x
O
y
M
P(a,b)
α
1
sinα=________;
cosα=________;
tanα=________;
b
a
b
a
在直角坐标系中,我们称以原点O为圆心,以单位长度为半径的圆为单位圆(unit circle).
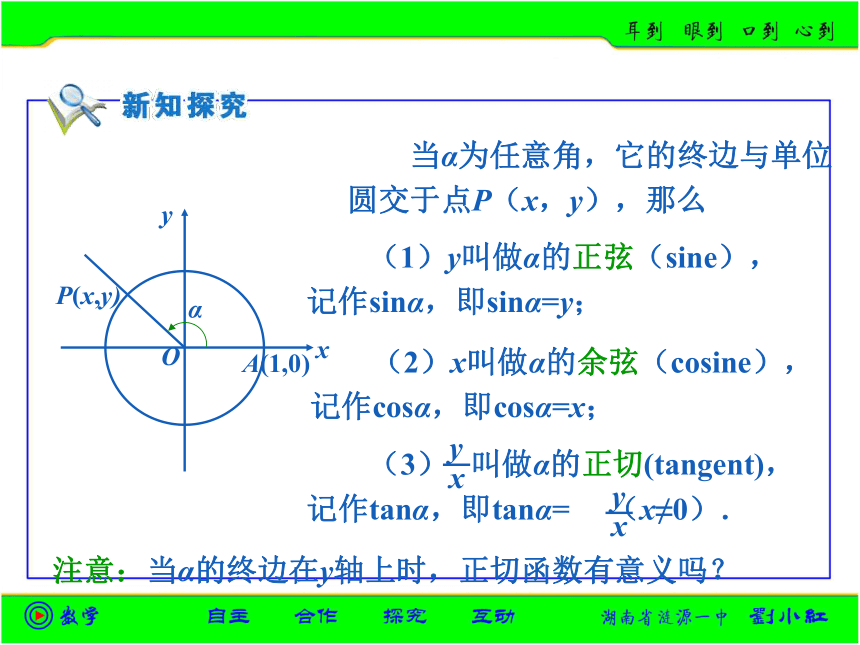
当α为任意角,它的终边与单位圆交于点P(x,y),那么
注意:当α的终边在y轴上时,正切函数有意义吗?
(1)y叫做α的正弦(sine),记作sinα,即sinα=y;
(2)x叫做α的余弦(cosine),记作cosα,即cosα=x;
(3) 叫做α的正切(tangent),
记作tanα,即tanα= (x≠0).
y
x
y
x
x
O
y
A(1,0)
P(x,y)
α
例1:求 的正弦、余弦和正切值.
5π
3
sin =
5π
3
√3
2
-
cos =
5π
3
1
2
tan =-√3
5π
3
解:在直角坐标系中,作∠AOB= (如下图).易知∠AOB的终边与单位圆的交点坐标为( , ).所以,
5π
3
√3
2
-
1
2
5π
3
x
O
y
A
B
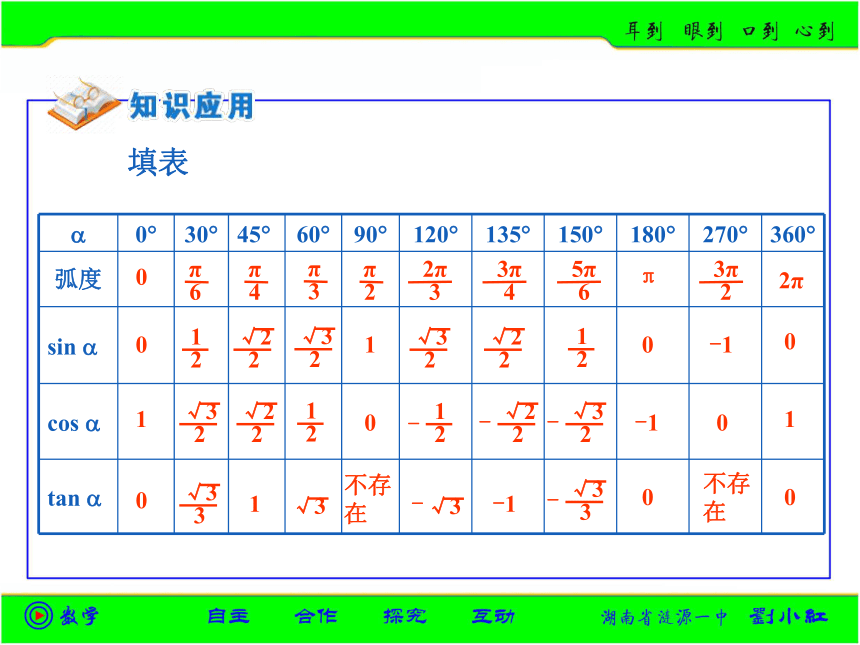
0 30 45 60 90 120 135 150 180 270 360
弧度
sin
cos
tan
填表
0
π
6
π
3
π
4
π
2
2π
3
5π
6
3π
4
3π
2
π
2π
0
0
1
√3
2
√3
1
2
1
2
√2
2
√3
2
1
0
0
0
0
0
0
√3
2
√2
2
1
2
-1
√2
2
√3
3
1
2
-
√2
2
-
√3
2
-
-1
1
1
√3
-
不存在
不存在
-1
√3
3
-
例2:已知角α的终边经过点P0(-3,-4),求角α的正弦、余弦和正切值.
分析:如下图,由△OMP∽△OM0P0,可求出相应的三角函数值.
x
O
y
M
P(x,y)
M0
P0 (-3,-4)
解:由已知可得:
OP0=√(-3)2+(-4)2=5
如图,设角α的终边与单位圆交于点P(x,y).分别过点P、P0做x轴的垂线MP、M0P0,则
你从这里发现了什么?
也可用角终边上任意一点的坐标来定义三角函数.
|M0P0|=4,|MP|=-y,
|OM0|=3,|OM|=-x ,
△OMP∽△OM0P0
于是,
sinα= y = = = =-
y
1
-|MP|
|OP|
|M0P0|
|OP0|
4
5
-
cosα= x= = = =-
x
1
-|OM|
|OP|
|OM0|
|OP0|
3
5
-
tanα= = =
y
x
sinα
cosα
4
3
可以用终边上任意一点的坐标来求三角函值,
1.已知角 的终边经过P(-3a, 4a),(a 0)
求2sin +cos -tan 的值.
解:依题意得:x=4a,y=-3a,
(1)当a>0时,角α是第四象限角,则
∴ r=√x2+y2=√(4a)2+(-3a)2=5|a|
sinα= = =
y
r
4a
5a
4
5
cosα= = -
x
r
3
5
tanα= = -
y
x
4
3
∴ 2sinα+cosα-tanα=
7
3
(2)当a<0时,角α是第二象限角,则
1.已知角 的终边经过P(-3a, 4a),(a 0)
求2sin +cos -tan 的值.
sinα= =- =-
y
r
4a
5a
4
5
cosα= =
x
r
3
5
tanα= = -
y
x
4
3
∴ 2sinα+cosα-tanα=
7
3
解:依题意得:x=4a,y=-3a,
∴ r=√x2+y2=√(4a)2+(-3a)2=5|a|
将正弦、余弦、正切函数在弧度制下的定义域填入下表.
三角函数 定义域
sinα
cosα
tanα
π
2
{x|x∈R,且x≠kπ+ ,k∈Z}
R
R
将正弦、余弦、正切函数的值在各象限的符号填入下图中.
O
x
y
sinα
+
( )
( )
( )
O
x
y
cosα
( )
( )
( )
( )
O
x
y
tanα
( )
( )
( )
( )
-
+
-
-
-
+
-
+
+
-
+
根据sinα、cosα、tanα在四个象限的值为正的情况,我们把它简记为:全STC.
x
O
y
在第一象限,三种函数的值全都为正
在第二象限,只有sinα的值为正
在第三象限,只有tanα的值为正
在第四象限,只有cosα的值为正
例3:求证:当且仅当下列不等式组成立时,角θ为第三象限角.
sinθ<0, ①
tanθ>0. ②
证明:我们证明如果①②式都成立,那么θ为第三象限角.
因为①式sinθ<0成立,所以θ角的终边可能位于第三或第四象限,也可能与y轴的非正半轴重合;
又因为②式tanθ>0成立,所以θ角的终边可能位于第一或第三象限.
例3:求证:当且仅当下列不等式组成立时,角θ为第三象限角.
因为①、②式都成立,所以θ角的终边只能位于第三象限,于是角θ为第三象限角.
你能自己试着证明反过来的情形吗?
sinθ<0, ①
tanθ>0. ②
你知道吗,三角函数有“周而复始”的变化规律.
作用:把求任意角的三角函数值转化为求0到2π角的三角函数值.
公式一说明终边相同的角的同一三角函数的值相等.
sin(α+k·2π)=sinα;
cos(α+k·2π)=cosα;
tan(α+k·2π)=tanα;
其中k∈Z.
公式一:
例4:确定下列三角函数值的符号,然后用计算器验证:
(1)cos250°;
(2)sin( );
-
π
4
(3)tan(-672°);
(4)tan3π.
解:
(1)因为250°是第三象限角,所以
cos250°<0
分析:要判断三角函数值的符号,只需看它是第几象限角.
(3)因为tan(-672°)=tan(48°-2×360°)=tan48°,而48°是第一象限角,所以
tan(-672°)>0
(4)因为tan3π=tan(π+2π)=tanπ,而π的终边在x轴上,所以
tan3π=0
sin( )<0
-
π
4
(2)因为 是第四象限角,所以
-
π
4
请同学们自己完成用计算器验证的过程.
已知( )sin2θ <1,则θ为第几象限角?
1
2
由 ( )sin2θ <1,有sin2θ>0.
1
2
故 2kπ<2θ<2kπ+π (k∈Z).
解:
所以θ为第一象限或第三象限角.
即 kπ<θπ
2
看图填空
你能用直角坐标系中角的终边上的点的坐标来表示锐角三角函数吗
α
b
a
sinα=_________
cosα=_________
tanα=_________
a2+b2
√
b
a2+b2
√
a
ba
想一想:对于确定的α,这三个比值会随P点在α的终边上的位置的改变而比值改变吗?
b
r
a
r
b
a
x
O
y
M
P(a,b)
α
r
sinα=________;
cosα=________;
tanα=________.
√
设锐角α与原点O重合,始边与x轴的非负半轴重合,且在它的终边上任取一点P(a,b)(除原点),则点P与原点的距离r = a2+b2>0.
取r=1,得到用直角坐标系内点的坐标表示的三角函数:
x
O
y
M
P(a,b)
α
1
sinα=________;
cosα=________;
tanα=________;
b
a
b
a
在直角坐标系中,我们称以原点O为圆心,以单位长度为半径的圆为单位圆(unit circle).
当α为任意角,它的终边与单位圆交于点P(x,y),那么
注意:当α的终边在y轴上时,正切函数有意义吗?
(1)y叫做α的正弦(sine),记作sinα,即sinα=y;
(2)x叫做α的余弦(cosine),记作cosα,即cosα=x;
(3) 叫做α的正切(tangent),
记作tanα,即tanα= (x≠0).
y
x
y
x
x
O
y
A(1,0)
P(x,y)
α
例1:求 的正弦、余弦和正切值.
5π
3
sin =
5π
3
√3
2
-
cos =
5π
3
1
2
tan =-√3
5π
3
解:在直角坐标系中,作∠AOB= (如下图).易知∠AOB的终边与单位圆的交点坐标为( , ).所以,
5π
3
√3
2
-
1
2
5π
3
x
O
y
A
B
0 30 45 60 90 120 135 150 180 270 360
弧度
sin
cos
tan
填表
0
π
6
π
3
π
4
π
2
2π
3
5π
6
3π
4
3π
2
π
2π
0
0
1
√3
2
√3
1
2
1
2
√2
2
√3
2
1
0
0
0
0
0
0
√3
2
√2
2
1
2
-1
√2
2
√3
3
1
2
-
√2
2
-
√3
2
-
-1
1
1
√3
-
不存在
不存在
-1
√3
3
-
例2:已知角α的终边经过点P0(-3,-4),求角α的正弦、余弦和正切值.
分析:如下图,由△OMP∽△OM0P0,可求出相应的三角函数值.
x
O
y
M
P(x,y)
M0
P0 (-3,-4)
解:由已知可得:
OP0=√(-3)2+(-4)2=5
如图,设角α的终边与单位圆交于点P(x,y).分别过点P、P0做x轴的垂线MP、M0P0,则
你从这里发现了什么?
也可用角终边上任意一点的坐标来定义三角函数.
|M0P0|=4,|MP|=-y,
|OM0|=3,|OM|=-x ,
△OMP∽△OM0P0
于是,
sinα= y = = = =-
y
1
-|MP|
|OP|
|M0P0|
|OP0|
4
5
-
cosα= x= = = =-
x
1
-|OM|
|OP|
|OM0|
|OP0|
3
5
-
tanα= = =
y
x
sinα
cosα
4
3
可以用终边上任意一点的坐标来求三角函值,
1.已知角 的终边经过P(-3a, 4a),(a 0)
求2sin +cos -tan 的值.
解:依题意得:x=4a,y=-3a,
(1)当a>0时,角α是第四象限角,则
∴ r=√x2+y2=√(4a)2+(-3a)2=5|a|
sinα= = =
y
r
4a
5a
4
5
cosα= = -
x
r
3
5
tanα= = -
y
x
4
3
∴ 2sinα+cosα-tanα=
7
3
(2)当a<0时,角α是第二象限角,则
1.已知角 的终边经过P(-3a, 4a),(a 0)
求2sin +cos -tan 的值.
sinα= =- =-
y
r
4a
5a
4
5
cosα= =
x
r
3
5
tanα= = -
y
x
4
3
∴ 2sinα+cosα-tanα=
7
3
解:依题意得:x=4a,y=-3a,
∴ r=√x2+y2=√(4a)2+(-3a)2=5|a|
将正弦、余弦、正切函数在弧度制下的定义域填入下表.
三角函数 定义域
sinα
cosα
tanα
π
2
{x|x∈R,且x≠kπ+ ,k∈Z}
R
R
将正弦、余弦、正切函数的值在各象限的符号填入下图中.
O
x
y
sinα
+
( )
( )
( )
O
x
y
cosα
( )
( )
( )
( )
O
x
y
tanα
( )
( )
( )
( )
-
+
-
-
-
+
-
+
+
-
+
根据sinα、cosα、tanα在四个象限的值为正的情况,我们把它简记为:全STC.
x
O
y
在第一象限,三种函数的值全都为正
在第二象限,只有sinα的值为正
在第三象限,只有tanα的值为正
在第四象限,只有cosα的值为正
例3:求证:当且仅当下列不等式组成立时,角θ为第三象限角.
sinθ<0, ①
tanθ>0. ②
证明:我们证明如果①②式都成立,那么θ为第三象限角.
因为①式sinθ<0成立,所以θ角的终边可能位于第三或第四象限,也可能与y轴的非正半轴重合;
又因为②式tanθ>0成立,所以θ角的终边可能位于第一或第三象限.
例3:求证:当且仅当下列不等式组成立时,角θ为第三象限角.
因为①、②式都成立,所以θ角的终边只能位于第三象限,于是角θ为第三象限角.
你能自己试着证明反过来的情形吗?
sinθ<0, ①
tanθ>0. ②
你知道吗,三角函数有“周而复始”的变化规律.
作用:把求任意角的三角函数值转化为求0到2π角的三角函数值.
公式一说明终边相同的角的同一三角函数的值相等.
sin(α+k·2π)=sinα;
cos(α+k·2π)=cosα;
tan(α+k·2π)=tanα;
其中k∈Z.
公式一:
例4:确定下列三角函数值的符号,然后用计算器验证:
(1)cos250°;
(2)sin( );
-
π
4
(3)tan(-672°);
(4)tan3π.
解:
(1)因为250°是第三象限角,所以
cos250°<0
分析:要判断三角函数值的符号,只需看它是第几象限角.
(3)因为tan(-672°)=tan(48°-2×360°)=tan48°,而48°是第一象限角,所以
tan(-672°)>0
(4)因为tan3π=tan(π+2π)=tanπ,而π的终边在x轴上,所以
tan3π=0
sin( )<0
-
π
4
(2)因为 是第四象限角,所以
-
π
4
请同学们自己完成用计算器验证的过程.
已知( )sin2θ <1,则θ为第几象限角?
1
2
由 ( )sin2θ <1,有sin2θ>0.
1
2
故 2kπ<2θ<2kπ+π (k∈Z).
解:
所以θ为第一象限或第三象限角.
即 kπ<θ
2
