1.2.2同角三角函数的基本关系

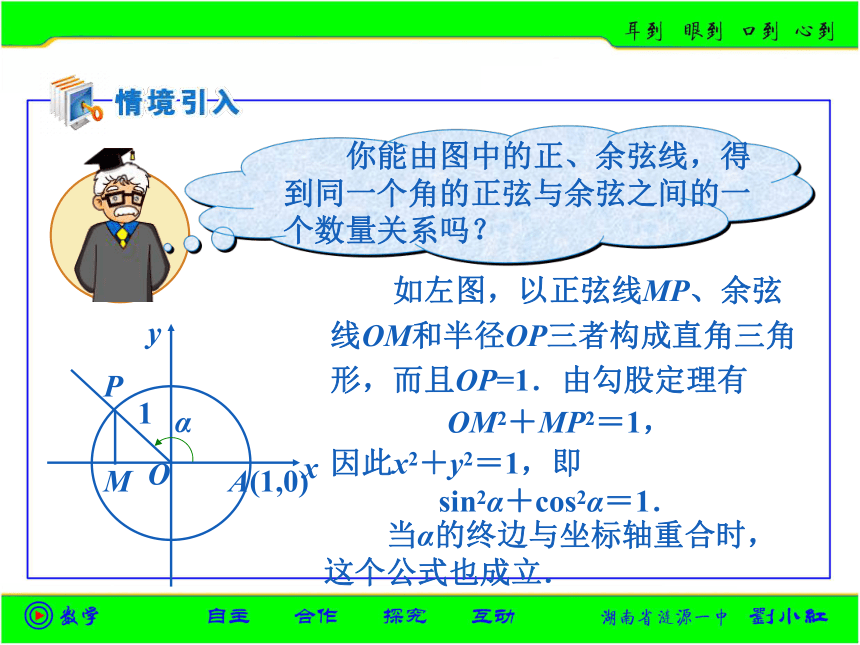
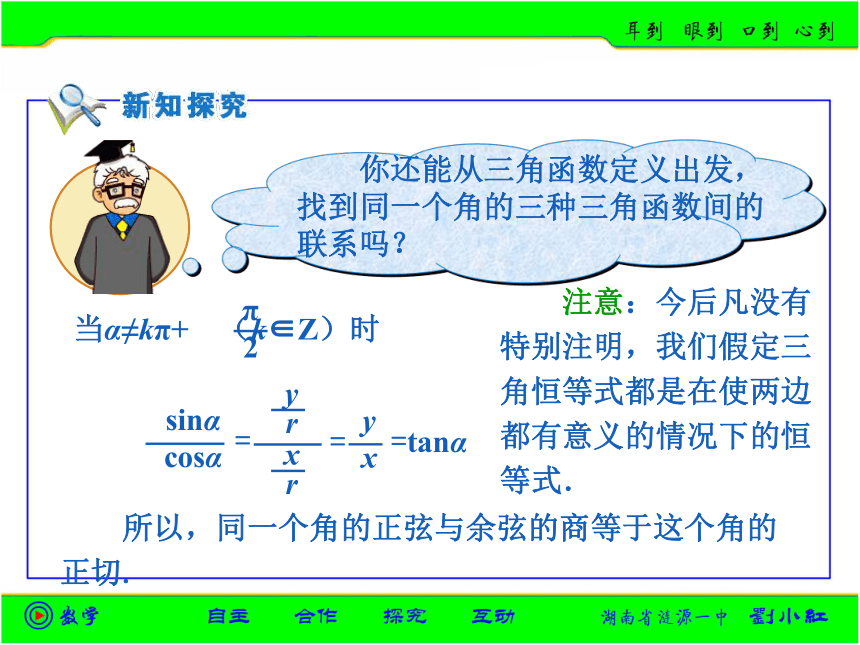
课件18张PPT。　　如左图，以正弦线MP、余弦线OM和半径OP三者构成直角三角形，而且OP=1．由勾股定理有OM2＋MP2＝1，因此x2＋y2＝1，即sin2α＋cos2α＝1．　　当α的终边与坐标轴重合时，这个公式也成立．由三角函数定义知：同一个角的正弦、余弦的平方和等于1.=1　　所以，同一个角的正弦与余弦的商等于这个角的正切.　　注意：今后凡没有特别注明，我们假定三角恒等式都是在使两边都有意义的情况下的恒等式．　　解：因为sinα＜0，sinα≠-1，所以α是第三或第四象限角．由sin2α+cos2α=1，得如果α是 第三象限角，那么cosα＜0，于是从而(2) 开方时，要注意符号．如果α是第四象限角，那么cosα＞0，于是从而提示：(1) 当角所在象限没定时，要分象限讨论；由cosx≠0，知sinx≠-1，所以1+sinx≠0，于是左边＝=右边例3：化简：解：原式＝1练习1．提示：1-2　　1) 这组公式是“同角”三角函数间的运算规律，所谓“同角”指只要角相同，与角的形式无关．　　2) 这组公式的应用要灵活，除顺用外，还应学会逆用、活用、变用．0解法一：切化弦所以，（2）sin2α+sinαcosα+2 cosα=2sinα（2）由sin2α＋cos2α＝1，和 cosα=2sinα（1）对原式，分子、分母均除以cosα，得解法二：弦化切（2）原式的分母为1，对原式分子、分母均除以cos2α，得sin2α+sinαcosα+2　　练习3．已知sinθ，cosθ是关于x的方程x2-ax+a=0（a∈R）的两个根，求sin3θ+ cos3θ的值．　　解：由已知得，判别式Δ≥0，即（-a）2-4a≥0，所以a≤0或a≥4∴ （sinθ+ cosθ）2 =1+2 sinθ cosθ =a2∴ sin3θ+cos3θ=（sinθ+cosθ）（ sin2θ- sinθcosθ+cos2θ ）证法一：∵ （1+cosx+sinx）cosx=cosx+cos2x+sinxcosx又 （1+cosx-sinx）（1+sinx ）=（1+cosx-sinx）+（sinx+sinxcosx-sin2x）= cosx+sinxcosx+（1-sin2x）= cosx+cos2x+sinxcosx又由合比性质得：证法二：由sin2x+cos2x=1，得证明：由①除以②得又因为θ锐角，所以　　练习5．已知sinθ=asinψ， tanθ=btanψ，其中θ为锐角．①2+③2得　　已知tanα为非零实数，用tanα来表示sinα，cosα的值．解：由得而得sinα= tanα·cosα