1.4.2 正弦函数、余弦函数的性质
文档属性
| 名称 | 1.4.2 正弦函数、余弦函数的性质 |  | |
| 格式 | rar | ||
| 文件大小 | 9.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-01-24 13:48:00 | ||
图片预览





文档简介
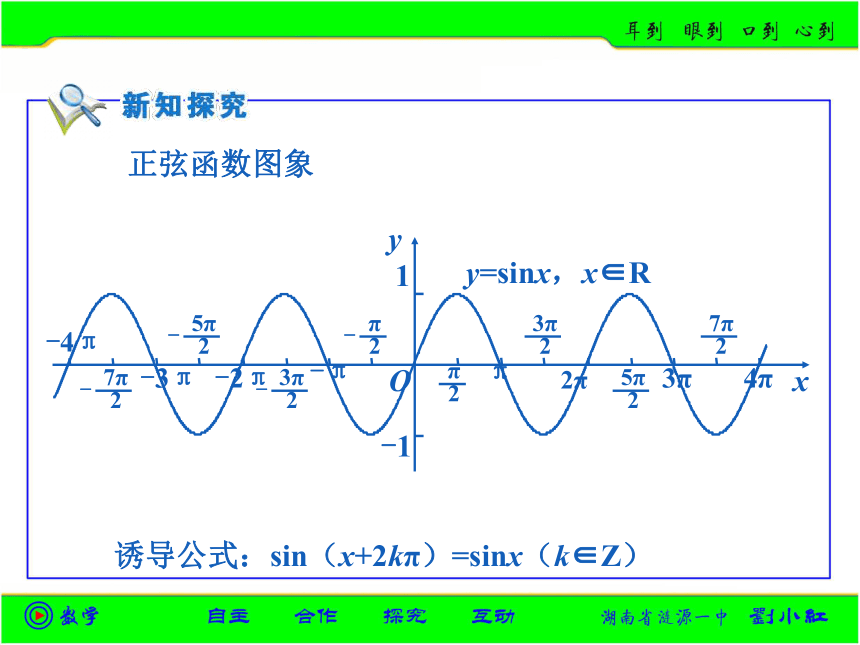
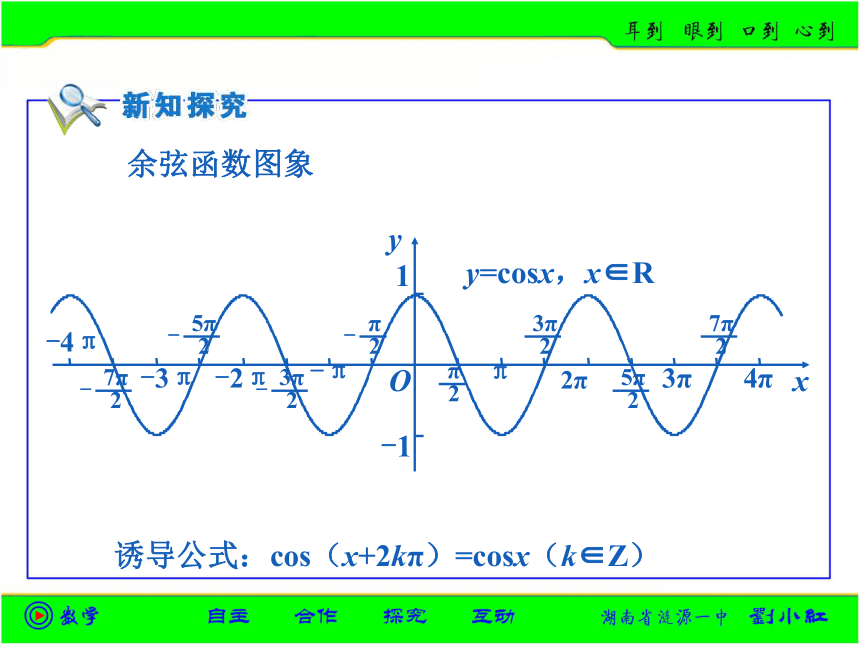
课件18张PPT。每年都有春夏秋冬,它们周而复始的变化着.生活中,许多事物都有“周而复始”的变化规律.正弦函数图象诱导公式:sin(x+2kπ)=sinx(k∈Z)y=sinx,x∈R诱导公式:cos(x+2kπ)=cosx(k∈Z)余弦函数图象y=cosx,x∈R 对于函数f(x)而言,如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有周期函数:那么函数f(x)就叫做周期函数(periodic fun_ction).f(x+T)=f(x),非零常数T叫做这个函数的周期(period). 如果在周期函数f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫做f(x)的最小正周期(minimal positive period). 特别地:今后所提及的周期,在没有特别说明的前提下,都是指函数的最小正周期.例1.判断2.y=|sinx|的周期是π且是偶函数.( )3.存在角x使得2cosx=3成立.( )√×× 对,因为|sin(x+π)|=|-sinx|=|sinx|.错,因为余弦函数的最大值为1.(1)求周期;(2)当x为何值时,函数有最值;(3)求函数的单调区间.解:(1)因为所以由周期函数的定义可知,原函数的周期为4π. 例3.利用三角函数的单调性,比较下列各组数的大小: 分析:利用三角函数的单调性比较两个同名三角函数值的大小,可以先用诱导公式将已知角化为同一单调区间内的角,然后再比较大小. 解:因为解:函数y=Asin(ωx+ψ) 从前面的例子可以看出,函数y=Asin(ωx+ψ),x∈R及函数y=Acos(ωx+ψ),x∈R(其中A,ω,ψ为常数,且A≠0,ω>0)的周期仅与自变量的系数有关.那么,如何用自变量的系数表示上述函数的周期呢?及函数y=Acos(ωx+ψ)的周期 事实上,令z=ωx+ψ,那么x∈R必须并且只需z∈R,且函数y=Asinz,z∈R及函数y=Acosz,z∈R的周期都是2π.由于成立的最小正数.从而,函数Asin[ω(x+T)+ψ]= Asin(ωx+ψ),Acos[ω(x+T)+ψ]= Acos(ωx+ψ)y=Asin(ωx+ψ),x∈R及函数y=Acos(ωx+ψ),x∈R
