1.4.3 正切函数的性质与图象
文档属性
| 名称 | 1.4.3 正切函数的性质与图象 |

|
|
| 格式 | rar | ||
| 文件大小 | 10.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-01-24 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
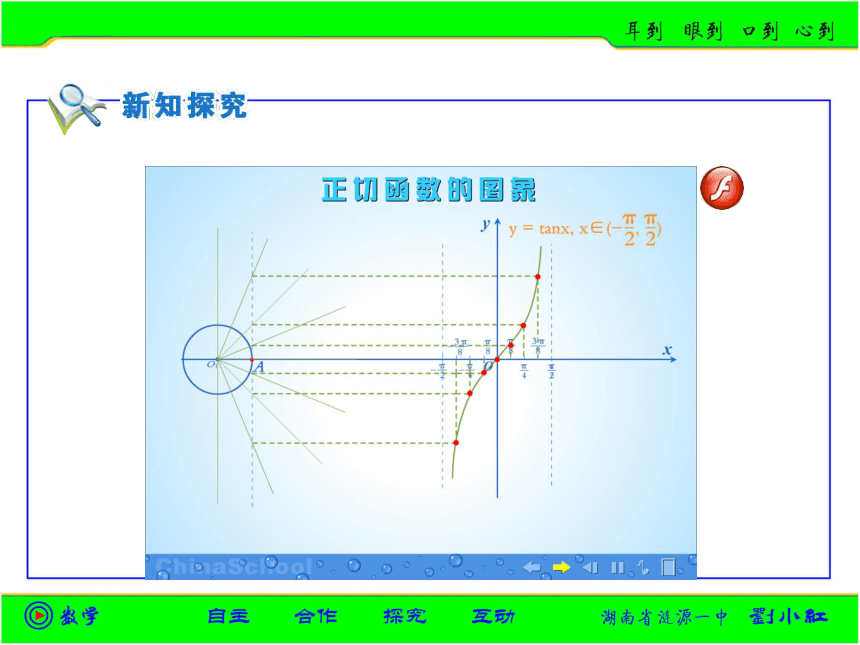
你能否根据研究正弦函数、余弦函数的图象及性质的经验,以同样的方法研究正切函数的图象与性质?
根据诱导公式填空:
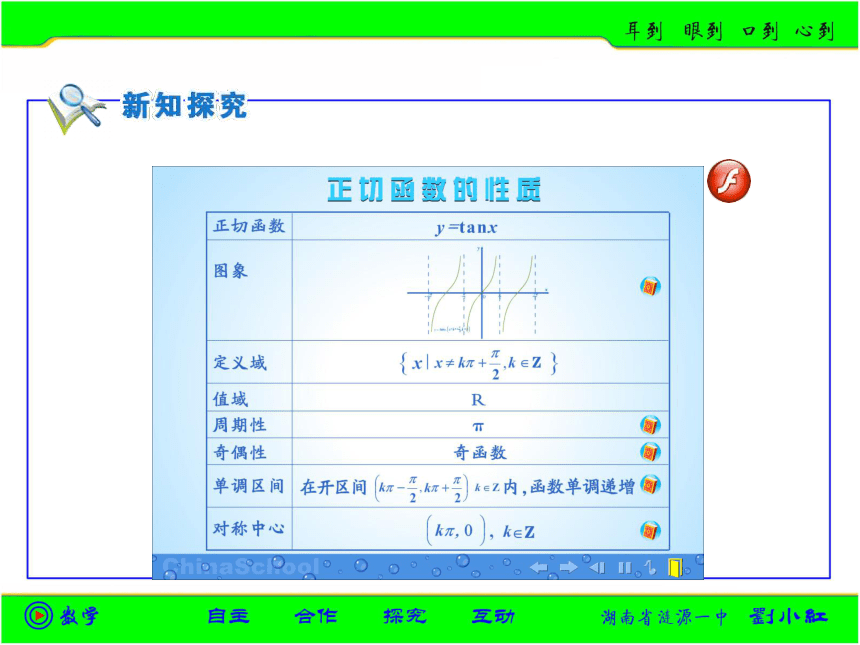
所以,正切函数是周期函数,且周期是______.
所以,正切函数是_______函数.
奇
1.tan(π+x)=______,x∈R,x≠ +kπ,k∈Z.
π
2
tanx
π
2.tan(-x)=______,x∈R,x≠ +kπ,k∈Z.
π
2
-tanx
例 求函数y=tan( x+ )的定义域、周期和单调区间.
π
2
π
3
解:函数的自变量x应满足
π
2
π
3
x+ ≠kπ+ ,k∈Z,
π
2
即
x≠2k+ ,k∈Z.
1
3
所以,函数的定义域是{x| }.
x≠2k+ ,k∈Z
1
3
因此函数的周期为2.
由于
f(x)=tan( x+ )=tan( x+ +π)
π
2
π
3
π
2
π
3
=tan[ (x+2)+ ]=f(x+2),
π
2
π
3
归纳:
形如函数y=Atan(ωx+ψ)的周期为 .
π
|ω|
由
π
2
- +kπ< x+ < +kπ,k∈Z解得
π
2
π
3
π
2
5
3
- +2k<x< +2k,k∈Z.
1
3
因此,函数的单调递增区间是
5
3
(- +2k, +2k),k∈Z.
1
3
1.观察正切曲线,写出满足下列条件的x值的范围:
(1)tanx>0;
(2)tanx=0;
(3)tanx<0.
π
2
π
1
y
O
x
-1
3π
2
π
2
-
-π
3π
2
-
-2π
5π
2
-
π
2
π
1
y
O
x
-1
3π
2
π
2
-
-π
3π
2
-
-2π
5π
2
-
解:根据图象可知:
(1)tanx>0时,{x|kπ<x< +kπ,k∈Z};
π
2
(2)tanx=0时,{x|x=kπ,k∈Z};
π
2
(3)tanx<0时,{x|- +kπ<x<kπ,k∈Z}.
2.设函数 f(x)(x∈R)是以2为最小正周期的周期函数,且x∈[0,2]时f(x)=(x-1)2.求f(3),
f( )的值.
7
2
解:由于f(x)以2为最小正周期,所以对任意x∈R,有f(x+2)=f(x).于是:
f(3)=f(1+2)=f(1)=(1-1)2 =0.
f( )=f( +2)=f( )=( -1)2 = .
7
2
3
2
3
2
3
2
1
4
(1)函数y=tanx是增函数. ( )
(2)能使tanx=0的x值是x=kπ,k∈Z.( )
3.判断:
错,正切函数在定义域上不具有单调性,只在
的每一个单调区间上是增函数.
(- +kπ, +kπ),k∈Z
π
2
π
2
×
√
对,因为正切函数的周期是π,而tanπ=0,所以能使tanx=0的x值是x=kπ,k∈Z.
(3)tan( )>tan( ).( )
13π
4
-
17π
5
-
√
对,利用诱导公式可将两个角转到同一单调区间上,从而可判断它们的正切值的大小.
4.填空
使y>1成立的x的集合是____________________________.
R
π
2
单调区间是_____________________________,
图象的对称中心是________________,
图象被直线____________________所隔开,
使y=1的x的取值集合是______________________,
函数 的定义域是_________________________,值域是___,周期是___.
y=-tan(2x- )
3π
4
x∈R,x≠ + ,k∈Z
kπ2
π
8
( + , + ),k∈Z
kπ2
π
8
kπ2
5π
8
( + ,0)
kπ2
3π
8
x= + ,k∈Z
kπ2
π
8
{x|x= + ,k∈Z}
π
4
kπ2
kπ2
{x| + <x< + ,k∈Z}
π
4
kπ2
5π8
2.当x∈(-π,π)时,原函数图象与直线y=4至少有2008个交点,求ω的取值范围.
已知函数 y=2tan(ωx+ ), (ω≠0) .
π
6
1.当ω=- 时,求函数的单调区间;
π
3
参考答案:
(1) 函数的单调区间是(-1+3k,2+3k),k∈Z;
(2) ω的取值范围是ω≥1004.
足球比赛时,有一种战术 “底传中”.即由边路球员带球从底线突破再把球传给中路球员.请你说说这种战术的优点.
你能否根据研究正弦函数、余弦函数的图象及性质的经验,以同样的方法研究正切函数的图象与性质?
根据诱导公式填空:
所以,正切函数是周期函数,且周期是______.
所以,正切函数是_______函数.
奇
1.tan(π+x)=______,x∈R,x≠ +kπ,k∈Z.
π
2
tanx
π
2.tan(-x)=______,x∈R,x≠ +kπ,k∈Z.
π
2
-tanx
例 求函数y=tan( x+ )的定义域、周期和单调区间.
π
2
π
3
解:函数的自变量x应满足
π
2
π
3
x+ ≠kπ+ ,k∈Z,
π
2
即
x≠2k+ ,k∈Z.
1
3
所以,函数的定义域是{x| }.
x≠2k+ ,k∈Z
1
3
因此函数的周期为2.
由于
f(x)=tan( x+ )=tan( x+ +π)
π
2
π
3
π
2
π
3
=tan[ (x+2)+ ]=f(x+2),
π
2
π
3
归纳:
形如函数y=Atan(ωx+ψ)的周期为 .
π
|ω|
由
π
2
- +kπ< x+ < +kπ,k∈Z解得
π
2
π
3
π
2
5
3
- +2k<x< +2k,k∈Z.
1
3
因此,函数的单调递增区间是
5
3
(- +2k, +2k),k∈Z.
1
3
1.观察正切曲线,写出满足下列条件的x值的范围:
(1)tanx>0;
(2)tanx=0;
(3)tanx<0.
π
2
π
1
y
O
x
-1
3π
2
π
2
-
-π
3π
2
-
-2π
5π
2
-
π
2
π
1
y
O
x
-1
3π
2
π
2
-
-π
3π
2
-
-2π
5π
2
-
解:根据图象可知:
(1)tanx>0时,{x|kπ<x< +kπ,k∈Z};
π
2
(2)tanx=0时,{x|x=kπ,k∈Z};
π
2
(3)tanx<0时,{x|- +kπ<x<kπ,k∈Z}.
2.设函数 f(x)(x∈R)是以2为最小正周期的周期函数,且x∈[0,2]时f(x)=(x-1)2.求f(3),
f( )的值.
7
2
解:由于f(x)以2为最小正周期,所以对任意x∈R,有f(x+2)=f(x).于是:
f(3)=f(1+2)=f(1)=(1-1)2 =0.
f( )=f( +2)=f( )=( -1)2 = .
7
2
3
2
3
2
3
2
1
4
(1)函数y=tanx是增函数. ( )
(2)能使tanx=0的x值是x=kπ,k∈Z.( )
3.判断:
错,正切函数在定义域上不具有单调性,只在
的每一个单调区间上是增函数.
(- +kπ, +kπ),k∈Z
π
2
π
2
×
√
对,因为正切函数的周期是π,而tanπ=0,所以能使tanx=0的x值是x=kπ,k∈Z.
(3)tan( )>tan( ).( )
13π
4
-
17π
5
-
√
对,利用诱导公式可将两个角转到同一单调区间上,从而可判断它们的正切值的大小.
4.填空
使y>1成立的x的集合是____________________________.
R
π
2
单调区间是_____________________________,
图象的对称中心是________________,
图象被直线____________________所隔开,
使y=1的x的取值集合是______________________,
函数 的定义域是_________________________,值域是___,周期是___.
y=-tan(2x- )
3π
4
x∈R,x≠ + ,k∈Z
kπ2
π
8
( + , + ),k∈Z
kπ2
π
8
kπ2
5π
8
( + ,0)
kπ2
3π
8
x= + ,k∈Z
kπ2
π
8
{x|x= + ,k∈Z}
π
4
kπ2
kπ2
{x| + <x< + ,k∈Z}
π
4
kπ2
5π8
2.当x∈(-π,π)时,原函数图象与直线y=4至少有2008个交点,求ω的取值范围.
已知函数 y=2tan(ωx+ ), (ω≠0) .
π
6
1.当ω=- 时,求函数的单调区间;
π
3
参考答案:
(1) 函数的单调区间是(-1+3k,2+3k),k∈Z;
(2) ω的取值范围是ω≥1004.
足球比赛时,有一种战术 “底传中”.即由边路球员带球从底线突破再把球传给中路球员.请你说说这种战术的优点.
