2.3.1-2 平面向量基本定理、正交分解及坐标表示
文档属性
| 名称 | 2.3.1-2 平面向量基本定理、正交分解及坐标表示 |

|
|
| 格式 | rar | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-01-25 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
思考:给定平面内任意两个向量e1,e2,请你作出向量3e1+2e2、e1-2e2.
平面内的任一向量是否都可以用形如λ1e1+λ2e2的向量表示呢?
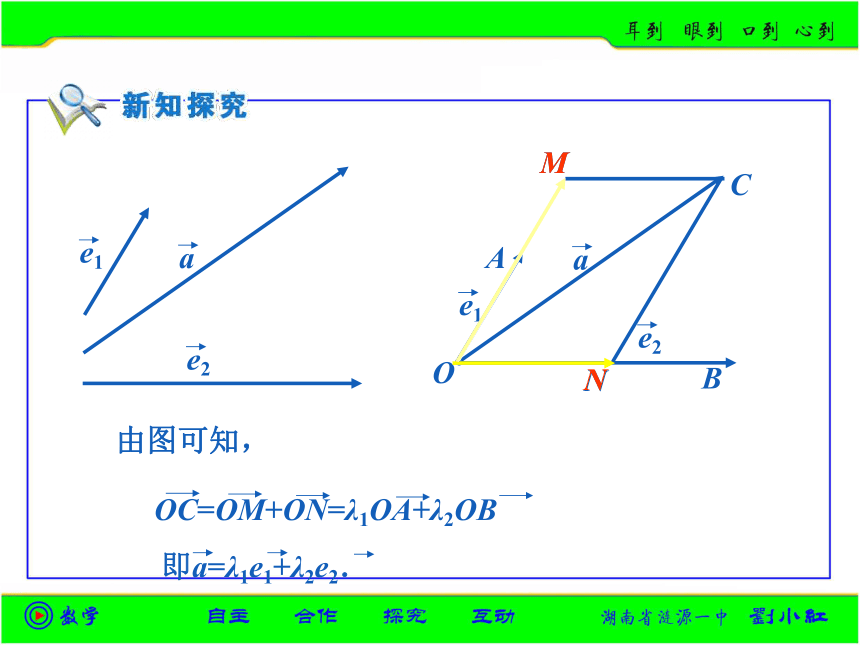
设e1、e2是同一平面内两个不共线的向量,a是这一平面内的任一向量,我们通过作图研究a与e1、e2之间的关系.
e1
e2
a
C
a
A
e1
e1
e2
a
O
N
M
B
e2
N
M
即a=λ1e1+λ2e2.
由图可知,
OC=OM+ON=λ1OA+λ2OB
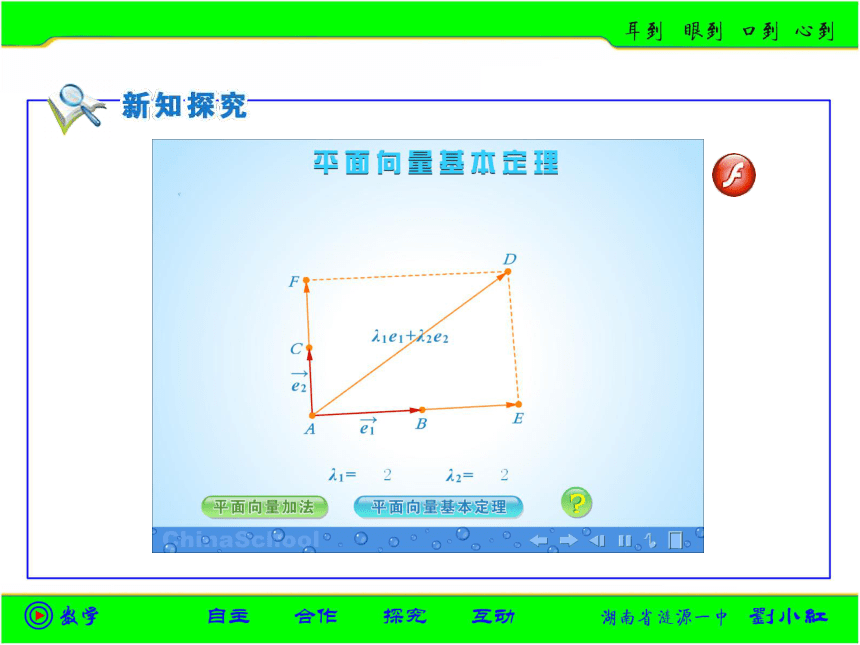
平面向量基本定理
如果e1、e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1、λ2,使
a=λ1e1+λ2e2.
我们把不共线的向量e1、e2叫做表示这一平面内所有向量的一组基底(base).
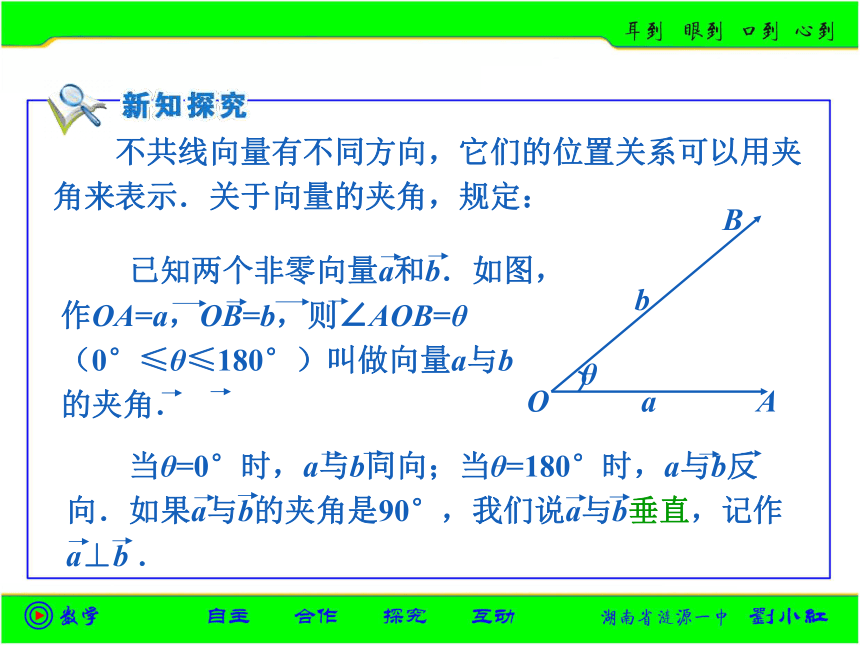
不共线向量有不同方向,它们的位置关系可以用夹角来表示.关于向量的夹角,规定:
O
a
b
B
A
θ
当θ=0°时,a与b同向;当θ=180°时,a与b反向.如果a与b的夹角是90°,我们说a与b垂直,记作a⊥b .
已知两个非零向量a和b.如图,作OA=a,OB=b,则∠AOB=θ(0°≤θ≤180°)叫做向量a与b的夹角.
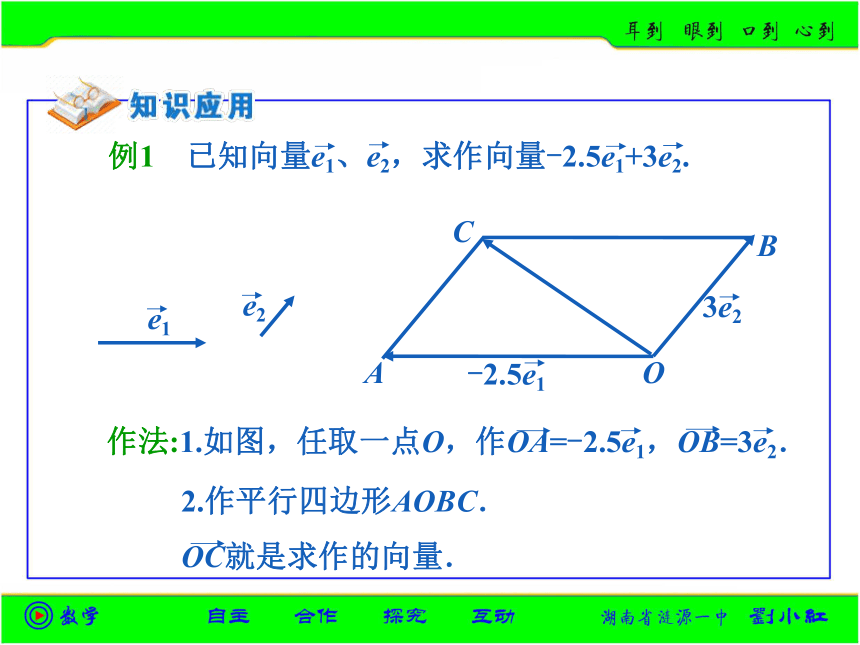
例1 已知向量e1、e2,求作向量-2.5e1+3e2.
e1
e2
3e2
-2.5e1
O
A
B
C
2.作平行四边形AOBC.
作法:1.如图,任取一点O,作OA=-2.5e1,OB=3e2.
OC就是求作的向量.
M
O
C
N
a
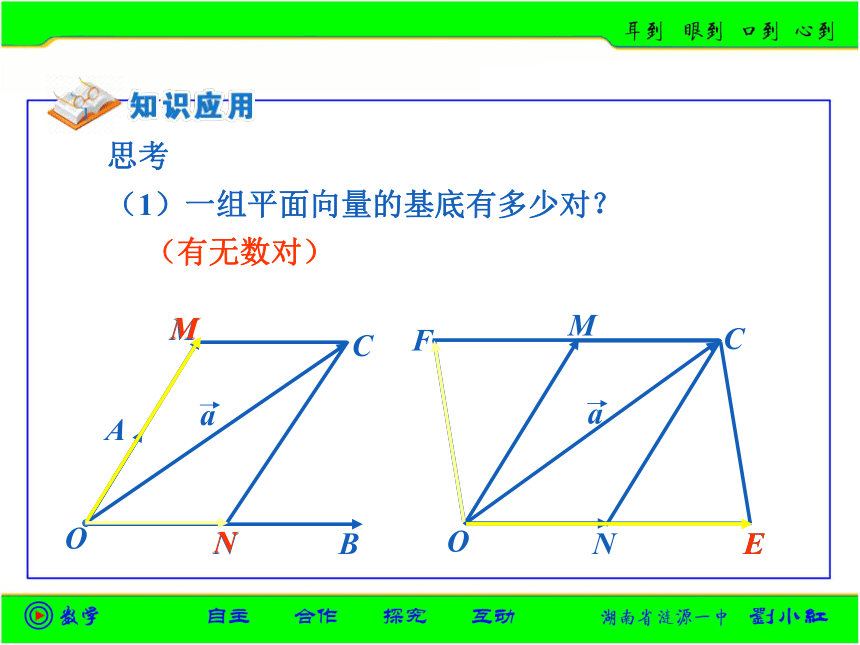
(1)一组平面向量的基底有多少对?
(有无数对)
思考
E
F
A
N
B
M
a
O
C
M
E
N
M
O
C
N
a
E
F
(2)若基底选取不同,则表示同一向量的实数λ1、λ2是否相同?
(可以不同,也可以相同)
A
B
OC=OF+OE
OC=2OA+OE
OC=2OB+ON
N
E
特别的,若a=0,则有且只有:
λ1=λ2=0
可使 0=λ1e1+λ2e2.
若λ1与λ2中只有一个为零,情况会是怎样?
特别的,若a与e1(e2)共线,则有λ2=0(λ1=0),使得:a=λ1e1+λ2e2.
如图,光滑斜面上一个木块受到重力G的作用,产生两个效果,一是木块受平行于斜面的力F1的作用,沿斜面下滑;一是木块产生垂直于斜面的压力F2.也就是说,重力G的效果等价于F1和F2的合力的效果,即G=F1+F2.G=F1+F2叫做把重力G分解.
类似地,由平面向量的基本定理,对平面上的任意向量a,均可以分解为不共线的两个向量λ1a1和λ2a2,使a=λ1a1+λ2a2.
在不共线的两个向量中,垂直是一种重要的情形.把一个向量分解为两个互相垂直的向量,叫做把向量正交分解.如图,重力G沿互相垂直的两个方向分解就是正交分解.
如图,在平面直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量i、j作为基底.对于平面内的一个向量a,由平面向量基本定理可知,有且只有一对实数x、y,使得
a=xi+yj.
①
O
x
y
i
j
a
a=(x,y),
②
其中x叫做a在x轴上的坐标,y叫做a在y轴上的坐标,②式叫做向量的坐标表示.
显然,i=(1,0),
j=(0,1),
0=(0,0).
这样,平面内的任一向量a都可由x、y唯一确定,我们把有序数对(x,y)叫做向量a的坐标,记作
O
x
y
i
j
a
如图,在直角坐标平面中,以原点O为起点作OA=a,则点A的位置由向量a唯一确定.
O
x
y
i
j
a
a
x
y
设OA=xi+yj,则向量OA的坐标(x,y)就是终点A的坐标;反过来,终点A的坐标(x,y)也就是向量OA的坐标.因此,在平面直角坐标系内,每一个平面向量都可以用一有序数对唯一表示.
d
a
x
i
O
y
j
1
2
3
4
5
-5
-4
-3
-2
-1
1
2
3
4
5
-1
-2
-3
-3
-4
-5
A
A1
A2
c
b
解:由图可知,
同理,
例2 如图,分别用基底i、j表示向量a、b、c、d,并求出它们的坐标.
a=AA1+AA2=2i+3j,
∴ a=(2,3).
b=-2i+3j=(-2,3);
c=-2i-3j=(-2,-3);
d=2i-3j=(2,-3).
练习
请大家在图中确一组基底,将其它向量用这组基底表示出来.
A
N
M
C
D
B
已知梯形ABCD,AB//CD,且AB= 2DC,M、N分别是DC,AB的中点.
A
N
M
C
D
B
解析:设AB=e1,AD=e2,则有:
DC= AB = e1
1
2
1
2
BC=BD+DC=(AD-AB)+DC=(e2-e1)+ e1=- e1+e2
1
2
1
2
MN=DN-DM=(AN-AD)- DC
1
2
= e1-e2- e1
1
2
1
4
= e1-e2
1
4
思考:给定平面内任意两个向量e1,e2,请你作出向量3e1+2e2、e1-2e2.
平面内的任一向量是否都可以用形如λ1e1+λ2e2的向量表示呢?
设e1、e2是同一平面内两个不共线的向量,a是这一平面内的任一向量,我们通过作图研究a与e1、e2之间的关系.
e1
e2
a
C
a
A
e1
e1
e2
a
O
N
M
B
e2
N
M
即a=λ1e1+λ2e2.
由图可知,
OC=OM+ON=λ1OA+λ2OB
平面向量基本定理
如果e1、e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1、λ2,使
a=λ1e1+λ2e2.
我们把不共线的向量e1、e2叫做表示这一平面内所有向量的一组基底(base).
不共线向量有不同方向,它们的位置关系可以用夹角来表示.关于向量的夹角,规定:
O
a
b
B
A
θ
当θ=0°时,a与b同向;当θ=180°时,a与b反向.如果a与b的夹角是90°,我们说a与b垂直,记作a⊥b .
已知两个非零向量a和b.如图,作OA=a,OB=b,则∠AOB=θ(0°≤θ≤180°)叫做向量a与b的夹角.
例1 已知向量e1、e2,求作向量-2.5e1+3e2.
e1
e2
3e2
-2.5e1
O
A
B
C
2.作平行四边形AOBC.
作法:1.如图,任取一点O,作OA=-2.5e1,OB=3e2.
OC就是求作的向量.
M
O
C
N
a
(1)一组平面向量的基底有多少对?
(有无数对)
思考
E
F
A
N
B
M
a
O
C
M
E
N
M
O
C
N
a
E
F
(2)若基底选取不同,则表示同一向量的实数λ1、λ2是否相同?
(可以不同,也可以相同)
A
B
OC=OF+OE
OC=2OA+OE
OC=2OB+ON
N
E
特别的,若a=0,则有且只有:
λ1=λ2=0
可使 0=λ1e1+λ2e2.
若λ1与λ2中只有一个为零,情况会是怎样?
特别的,若a与e1(e2)共线,则有λ2=0(λ1=0),使得:a=λ1e1+λ2e2.
如图,光滑斜面上一个木块受到重力G的作用,产生两个效果,一是木块受平行于斜面的力F1的作用,沿斜面下滑;一是木块产生垂直于斜面的压力F2.也就是说,重力G的效果等价于F1和F2的合力的效果,即G=F1+F2.G=F1+F2叫做把重力G分解.
类似地,由平面向量的基本定理,对平面上的任意向量a,均可以分解为不共线的两个向量λ1a1和λ2a2,使a=λ1a1+λ2a2.
在不共线的两个向量中,垂直是一种重要的情形.把一个向量分解为两个互相垂直的向量,叫做把向量正交分解.如图,重力G沿互相垂直的两个方向分解就是正交分解.
如图,在平面直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量i、j作为基底.对于平面内的一个向量a,由平面向量基本定理可知,有且只有一对实数x、y,使得
a=xi+yj.
①
O
x
y
i
j
a
a=(x,y),
②
其中x叫做a在x轴上的坐标,y叫做a在y轴上的坐标,②式叫做向量的坐标表示.
显然,i=(1,0),
j=(0,1),
0=(0,0).
这样,平面内的任一向量a都可由x、y唯一确定,我们把有序数对(x,y)叫做向量a的坐标,记作
O
x
y
i
j
a
如图,在直角坐标平面中,以原点O为起点作OA=a,则点A的位置由向量a唯一确定.
O
x
y
i
j
a
a
x
y
设OA=xi+yj,则向量OA的坐标(x,y)就是终点A的坐标;反过来,终点A的坐标(x,y)也就是向量OA的坐标.因此,在平面直角坐标系内,每一个平面向量都可以用一有序数对唯一表示.
d
a
x
i
O
y
j
1
2
3
4
5
-5
-4
-3
-2
-1
1
2
3
4
5
-1
-2
-3
-3
-4
-5
A
A1
A2
c
b
解:由图可知,
同理,
例2 如图,分别用基底i、j表示向量a、b、c、d,并求出它们的坐标.
a=AA1+AA2=2i+3j,
∴ a=(2,3).
b=-2i+3j=(-2,3);
c=-2i-3j=(-2,-3);
d=2i-3j=(2,-3).
练习
请大家在图中确一组基底,将其它向量用这组基底表示出来.
A
N
M
C
D
B
已知梯形ABCD,AB//CD,且AB= 2DC,M、N分别是DC,AB的中点.
A
N
M
C
D
B
解析:设AB=e1,AD=e2,则有:
DC= AB = e1
1
2
1
2
BC=BD+DC=(AD-AB)+DC=(e2-e1)+ e1=- e1+e2
1
2
1
2
MN=DN-DM=(AN-AD)- DC
1
2
= e1-e2- e1
1
2
1
4
= e1-e2
1
4
