勾股定理期末复习讲义
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
勾股定理期末复习讲义
提要:本节内容的重点是勾股定理及其应用.勾股定理是解几何中有关线段计算问题的重要依据,也是以后学习解直角三角形的主要依据之一,在生产生活实际中用途很大,它不仅在数学中,而且在其他自然科学中也被广泛地应用.
本节内容的难点是勾股定理的证明.勾股定理的证明方法有多种,课本是通过构造图形,利用面积相等来证明的这里还涉及到了解决几何问题的方法之一:面积法。割补(……陌生的名词么,但是我们用过)的思想也要值得我们去注意.
【知识结构】
1.勾股定理:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.……由这句话你能联想到那些东西?
2.勾股定理的逆定理:
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
……这个定理有什么用?
3.勾股数
能够成为直角三角形三条边长的三个正整数,称为勾股数.
……你记得几组勾股数?
显然,若(a,b,c)为一组基本勾股数,则(ka,kb,kc)也为勾股数,其中k为正整数.……如果熟练这个结论是不是能提高解题速度呢
4. 利用尺规画出长度是无理数的线段.……最简单的就是画了,知道画吧
5. 勾股定理及其逆定理的应用.……蚂蚁怎样走最近
【注意】
1.勾股定理的证明,是利用图形的割补变化,通过有关面积的数量关系进行证明的方法.
2.在应用勾股定理时,要注意在直角三角形的前提条件,分清直角三角形的直角边和斜边.
3. 在应用勾股定理逆定理时,先要确定最长边,再计算两条较短边的平方和是否等于最长边的平方,最后确定三角形是不是直角三角形.
4. 本章关联的知识点:实数的运算,三角形,四边形,图形变换,解方程等
【基础训练A】
1.三角形三边之比分别为①1:2:3,②3:4:5;③1.5:2:2.5,④4:5:6,其中可以构成直角三角形的有( )
A.1个 B.2个 C.3个 D.4个
2. 若线段a、b、c能构成直角三角形,则它们的比为( )
A.2:3:4 B.3:4:6 C.5:12:13 D.4:6:7
3.下面四组数中是勾股数的有( )
(1)1.5,2.5,2 (2),,2
(3)12,16,20 (4)0.5,1.2,1.3
A.1组 B.2组 C.3组 D.4组
4. △ABC中,∠C=90°,c=10,a:b=3:4,则a=______,b=_______.
5. 在△ABC中∠C=90°,AB=10,AC=6,则另一边BC=________,面积为______, AB边上的高为________;
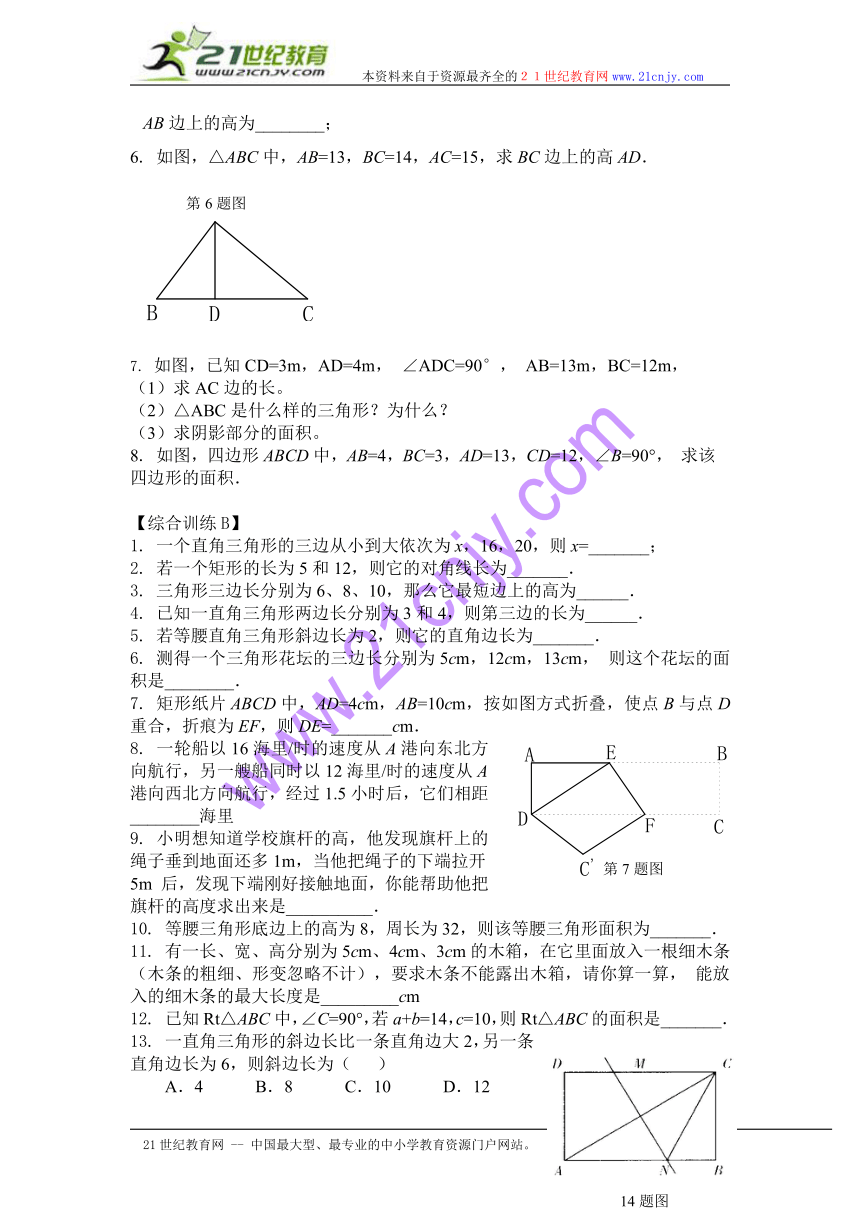
6. 如图,△ABC中,AB=13,BC=14,AC=15,求BC边上的高AD.
7. 如图,已知CD=3m,AD=4m, ∠ADC=90°, AB=13m,BC=12m,
(1)求AC边的长。
(2)△ABC是什么样的三角形?为什么?
(3)求阴影部分的面积。
8. 如图,四边形ABCD中,AB=4,BC=3,AD=13,CD=12,∠B=90°,求该四边形的面积.
【综合训练B】
1. 一个直角三角形的三边从小到大依次为x,16,20,则x=_______;
2. 若一个矩形的长为5和12,则它的对角线长为_______.
3. 三角形三边长分别为6、8、10,那么它最短边上的高为______.
4. 已知一直角三角形两边长分别为3和4,则第三边的长为______.
5. 若等腰直角三角形斜边长为2,则它的直角边长为_______.
6. 测得一个三角形花坛的三边长分别为5cm,12cm,13cm,则这个花坛的面积是________.
7. 矩形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,则DE=_______cm.
8. 一轮船以16海里/时的速度从A港向东北方向航行,另一艘船同时以12海里/时的速度从A港向西北方向航行,经过1.5小时后,它们相距________海里
9. 小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多1m,当他把绳子的下端拉开5m后,发现下端刚好接触地面,你能帮助他把旗杆的高度求出来是__________.
10. 等腰三角形底边上的高为8,周长为32,则该等腰三角形面积为_______.
11. 有一长、宽、高分别为5cm、4cm、3cm的木箱,在它里面放入一根细木条(木条的粗细、形变忽略不计),要求木条不能露出木箱,请你算一算,能放入的细木条的最大长度是_________cm
12. 已知Rt△ABC中,∠C=90°,若a+b=14,c=10,则Rt△ABC的面积是_______.
13. 一直角三角形的斜边长比一条直角边大2,另一条直角边长为6,则斜边长为( )
A.4 B.8 C.10 D.12
14. 如图,长方形ABCD中,AB=4,BC=3,将其沿直线MN折叠,使点C与点A重合,则CN的长为( )
A. B. C. D.
15. 如图所示,A、B、C均为正方形,B、C的面积分别为64、180,则A的面积为
16. 某农户有一块如图所示的土地,已知∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m。你能帮该农户计算这块土地的面积吗?
在△ABC中∠C=90°,AB=10,AC=6,则另一边BC=________,面积为______, AB边上的高为________;
【想一想】小强家有一块三角形的菜地,量得两边长分别为13m,16m,第三边上的高为12m,请你计算这块菜地的面积。
17. 如图所示,有一块直角三角形纸片,两直角边分别为:AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于
18. 如图所示,某人到一个荒岛上去探宝,在A处登陆后,往东走8km,又往北走2km,遇到障碍后又往西走3km,再折向北方走到5km处往东一拐,仅1km就找到了宝藏,问:登陆点(A处)到宝藏埋藏点(B处)的直线距离是多少?
19. 已知,如图所示,折叠长方形的一边AD,使点D落在BC边的点F处,如果AB=8cm,BC=10cm,求EC的长.
20.某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80米,BC=60米,若线段CD是一条小渠,且D点在边AB上,已知水渠的造价为10元/米,问D点在距A点多远处时,水渠的造价最低?最低造价是多少?
( http: / / )
21.如图,圆柱高为8cm,底面半径为2 cm,一只蚂蚁从A点爬到B点吃食物,则蚂蚁的最短行程是( )(本题中的π取3)
A.20 B.10 C.14 D.无法确定
22.如图,在边长为c的正方形中,有四个斜边为c的全等直角三角形,已知其直角边长为a,b.利用这个图试说明勾股定理
23.如图1所示,在一个有4×4个小正方形组成的正方形网格中,阴影部分的面积与正方形ABCD的面积比是( )
A、3:4 B、5:8 C、9:16 D、1:2
看看其他的面积怎么求?是不是还能联想到第三章旋转与平移,第五章位置的确定里面我们也有见过类似的东东?
【一刻钟自测】
1、 一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是 。
2、 三角形的两边长分别是6和8,要使这个三角形是直角三角形,则第三条边长可以是
3、 △ABC的三边之比是1∶1∶,则△ABC是 __________三角形
4、 已知一个直角三角形的两条直角边分别为5cm、12cm,那么这个直角三角形斜边上的高为____
5、 如图将一根长24cm的筷子,置于底面直径为8cm,高为15cm的圆柱形水杯中,设筷子露在杯子外面的长度是h cm,则h的取值范围是________
6、 已知,如图所示,折叠长方形的一边AD,使点D落在
BC边的点F处,如果AB=8cm, BC=10cm,求EC的长.
第6题图
第7题图
14题图
第16题图
第15题图
第19题图
第18题图
第17题图
C
第22题图
第21题图
第20题图
图4
图1
图2
图3
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
勾股定理期末复习讲义
提要:本节内容的重点是勾股定理及其应用.勾股定理是解几何中有关线段计算问题的重要依据,也是以后学习解直角三角形的主要依据之一,在生产生活实际中用途很大,它不仅在数学中,而且在其他自然科学中也被广泛地应用.
本节内容的难点是勾股定理的证明.勾股定理的证明方法有多种,课本是通过构造图形,利用面积相等来证明的这里还涉及到了解决几何问题的方法之一:面积法。割补(……陌生的名词么,但是我们用过)的思想也要值得我们去注意.
【知识结构】
1.勾股定理:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.……由这句话你能联想到那些东西?
2.勾股定理的逆定理:
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
……这个定理有什么用?
3.勾股数
能够成为直角三角形三条边长的三个正整数,称为勾股数.
……你记得几组勾股数?
显然,若(a,b,c)为一组基本勾股数,则(ka,kb,kc)也为勾股数,其中k为正整数.……如果熟练这个结论是不是能提高解题速度呢
4. 利用尺规画出长度是无理数的线段.……最简单的就是画了,知道画吧
5. 勾股定理及其逆定理的应用.……蚂蚁怎样走最近
【注意】
1.勾股定理的证明,是利用图形的割补变化,通过有关面积的数量关系进行证明的方法.
2.在应用勾股定理时,要注意在直角三角形的前提条件,分清直角三角形的直角边和斜边.
3. 在应用勾股定理逆定理时,先要确定最长边,再计算两条较短边的平方和是否等于最长边的平方,最后确定三角形是不是直角三角形.
4. 本章关联的知识点:实数的运算,三角形,四边形,图形变换,解方程等
【基础训练A】
1.三角形三边之比分别为①1:2:3,②3:4:5;③1.5:2:2.5,④4:5:6,其中可以构成直角三角形的有( )
A.1个 B.2个 C.3个 D.4个
2. 若线段a、b、c能构成直角三角形,则它们的比为( )
A.2:3:4 B.3:4:6 C.5:12:13 D.4:6:7
3.下面四组数中是勾股数的有( )
(1)1.5,2.5,2 (2),,2
(3)12,16,20 (4)0.5,1.2,1.3
A.1组 B.2组 C.3组 D.4组
4. △ABC中,∠C=90°,c=10,a:b=3:4,则a=______,b=_______.
5. 在△ABC中∠C=90°,AB=10,AC=6,则另一边BC=________,面积为______, AB边上的高为________;
6. 如图,△ABC中,AB=13,BC=14,AC=15,求BC边上的高AD.
7. 如图,已知CD=3m,AD=4m, ∠ADC=90°, AB=13m,BC=12m,
(1)求AC边的长。
(2)△ABC是什么样的三角形?为什么?
(3)求阴影部分的面积。
8. 如图,四边形ABCD中,AB=4,BC=3,AD=13,CD=12,∠B=90°,求该四边形的面积.
【综合训练B】
1. 一个直角三角形的三边从小到大依次为x,16,20,则x=_______;
2. 若一个矩形的长为5和12,则它的对角线长为_______.
3. 三角形三边长分别为6、8、10,那么它最短边上的高为______.
4. 已知一直角三角形两边长分别为3和4,则第三边的长为______.
5. 若等腰直角三角形斜边长为2,则它的直角边长为_______.
6. 测得一个三角形花坛的三边长分别为5cm,12cm,13cm,则这个花坛的面积是________.
7. 矩形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,则DE=_______cm.
8. 一轮船以16海里/时的速度从A港向东北方向航行,另一艘船同时以12海里/时的速度从A港向西北方向航行,经过1.5小时后,它们相距________海里
9. 小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多1m,当他把绳子的下端拉开5m后,发现下端刚好接触地面,你能帮助他把旗杆的高度求出来是__________.
10. 等腰三角形底边上的高为8,周长为32,则该等腰三角形面积为_______.
11. 有一长、宽、高分别为5cm、4cm、3cm的木箱,在它里面放入一根细木条(木条的粗细、形变忽略不计),要求木条不能露出木箱,请你算一算,能放入的细木条的最大长度是_________cm
12. 已知Rt△ABC中,∠C=90°,若a+b=14,c=10,则Rt△ABC的面积是_______.
13. 一直角三角形的斜边长比一条直角边大2,另一条直角边长为6,则斜边长为( )
A.4 B.8 C.10 D.12
14. 如图,长方形ABCD中,AB=4,BC=3,将其沿直线MN折叠,使点C与点A重合,则CN的长为( )
A. B. C. D.
15. 如图所示,A、B、C均为正方形,B、C的面积分别为64、180,则A的面积为
16. 某农户有一块如图所示的土地,已知∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m。你能帮该农户计算这块土地的面积吗?
在△ABC中∠C=90°,AB=10,AC=6,则另一边BC=________,面积为______, AB边上的高为________;
【想一想】小强家有一块三角形的菜地,量得两边长分别为13m,16m,第三边上的高为12m,请你计算这块菜地的面积。
17. 如图所示,有一块直角三角形纸片,两直角边分别为:AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于
18. 如图所示,某人到一个荒岛上去探宝,在A处登陆后,往东走8km,又往北走2km,遇到障碍后又往西走3km,再折向北方走到5km处往东一拐,仅1km就找到了宝藏,问:登陆点(A处)到宝藏埋藏点(B处)的直线距离是多少?
19. 已知,如图所示,折叠长方形的一边AD,使点D落在BC边的点F处,如果AB=8cm,BC=10cm,求EC的长.
20.某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80米,BC=60米,若线段CD是一条小渠,且D点在边AB上,已知水渠的造价为10元/米,问D点在距A点多远处时,水渠的造价最低?最低造价是多少?
( http: / / )
21.如图,圆柱高为8cm,底面半径为2 cm,一只蚂蚁从A点爬到B点吃食物,则蚂蚁的最短行程是( )(本题中的π取3)
A.20 B.10 C.14 D.无法确定
22.如图,在边长为c的正方形中,有四个斜边为c的全等直角三角形,已知其直角边长为a,b.利用这个图试说明勾股定理
23.如图1所示,在一个有4×4个小正方形组成的正方形网格中,阴影部分的面积与正方形ABCD的面积比是( )
A、3:4 B、5:8 C、9:16 D、1:2
看看其他的面积怎么求?是不是还能联想到第三章旋转与平移,第五章位置的确定里面我们也有见过类似的东东?
【一刻钟自测】
1、 一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是 。
2、 三角形的两边长分别是6和8,要使这个三角形是直角三角形,则第三条边长可以是
3、 △ABC的三边之比是1∶1∶,则△ABC是 __________三角形
4、 已知一个直角三角形的两条直角边分别为5cm、12cm,那么这个直角三角形斜边上的高为____
5、 如图将一根长24cm的筷子,置于底面直径为8cm,高为15cm的圆柱形水杯中,设筷子露在杯子外面的长度是h cm,则h的取值范围是________
6、 已知,如图所示,折叠长方形的一边AD,使点D落在
BC边的点F处,如果AB=8cm, BC=10cm,求EC的长.
第6题图
第7题图
14题图
第16题图
第15题图
第19题图
第18题图
第17题图
C
第22题图
第21题图
第20题图
图4
图1
图2
图3
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
