5.1.1 相交线
图片预览
文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
5.1.1 相交线
◆知能点分类训练
知能点1 邻补角的概念及性质
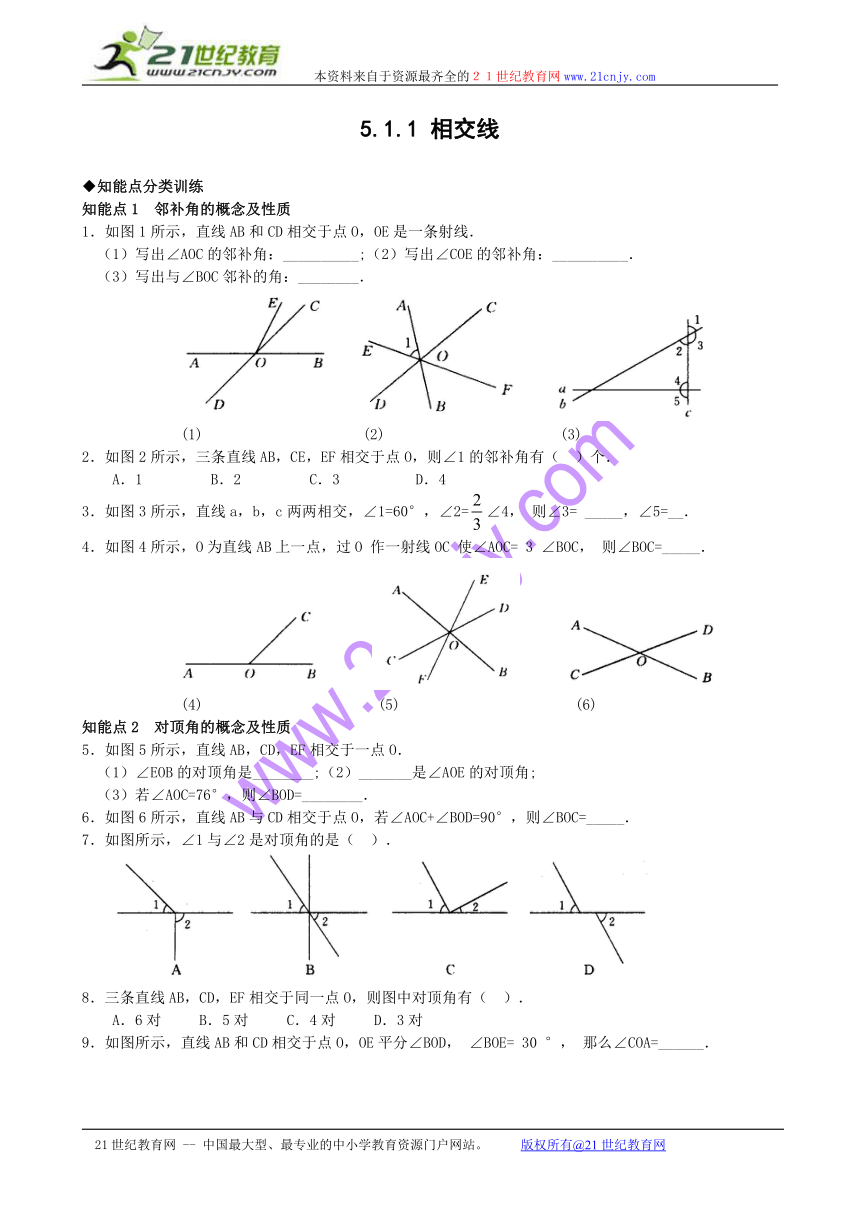
1.如图1所示,直线AB和CD相交于点O,OE是一条射线.
(1)写出∠AOC的邻补角:__________;(2)写出∠COE的邻补角:__________.
(3)写出与∠BOC邻补的角:________.
( http: / / )
(1) (2) (3)
2.如图2所示,三条直线AB,CE,EF相交于点O,则∠1的邻补角有( )个.
A.1 B.2 C.3 D.4
3.如图3所示,直线a,b,c两两相交,∠1=60°,∠2=∠4,则∠3=_____,∠5=__.
4.如图4所示,O为直线AB上一点,过O作一射线OC使∠AOC=3∠BOC,则∠BOC=_____.
(4) (5) (6)
知能点2 对顶角的概念及性质
5.如图5所示,直线AB,CD,EF相交于一点O.
(1)∠EOB的对顶角是________;(2)_______是∠AOE的对顶角;
(3)若∠AOC=76°,则∠BOD=________.
6.如图6所示,直线AB与CD相交于点O,若∠AOC+∠BOD=90°,则∠BOC=_____.
7.如图所示,∠1与∠2是对顶角的是( ).
( http: / / )
8.三条直线AB,CD,EF相交于同一点O,则图中对顶角有( ).
A.6对 B.5对 C.4对 D.3对
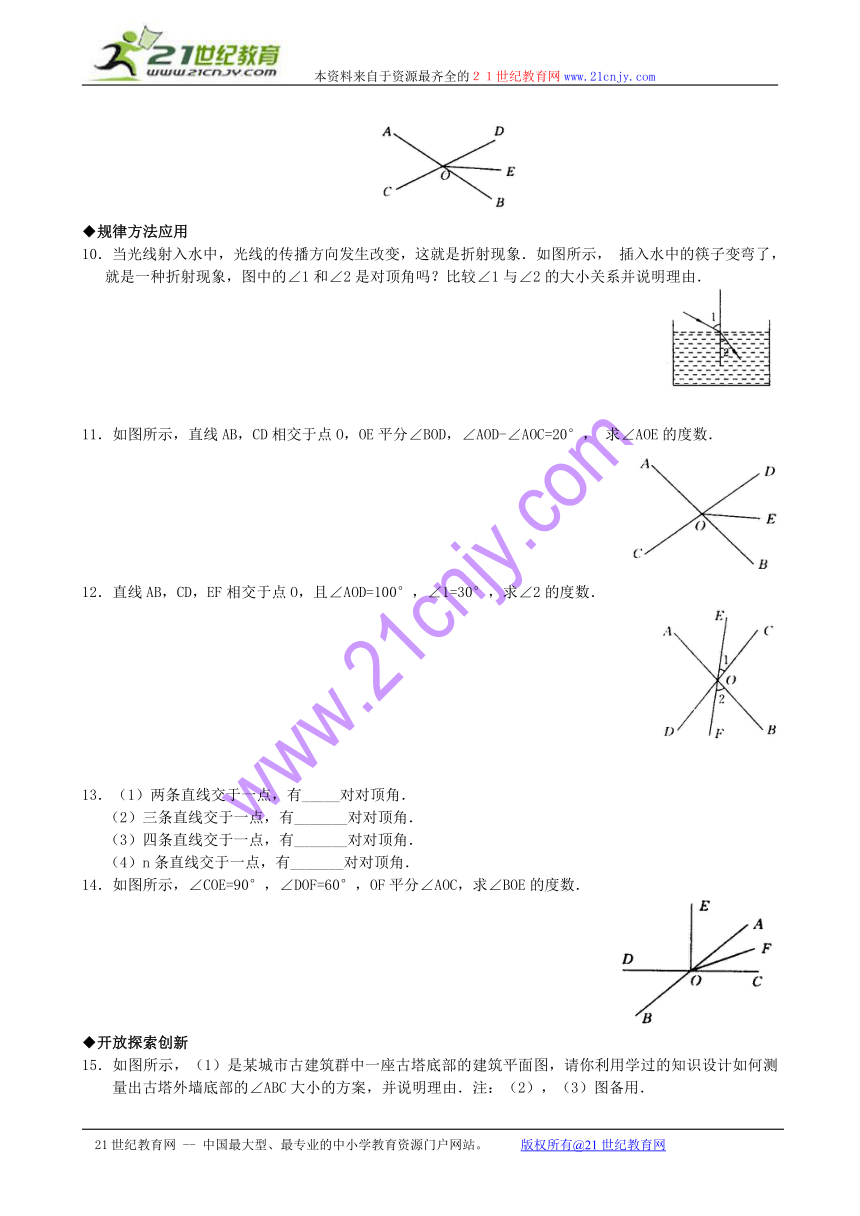
9.如图所示,直线AB和CD相交于点O,OE平分∠BOD,∠BOE=30°,那么∠COA=______.
◆规律方法应用
10.当光线射入水中,光线的传播方向发生改变,这就是折射现象.如图所示,插入水中的筷子变弯了,就是一种折射现象,图中的∠1和∠2是对顶角吗?比较∠1与∠2的大小关系并说明理由.
( http: / / )
11.如图所示,直线AB,CD相交于点O,OE平分∠BOD,∠AOD-∠AOC=20°,求∠AOE的度数.
12.直线AB,CD,EF相交于点O,且∠AOD=100°,∠1=30°,求∠2的度数.
13.(1)两条直线交于一点,有_____对对顶角.
(2)三条直线交于一点,有_______对对顶角.
(3)四条直线交于一点,有_______对对顶角.
(4)n条直线交于一点,有_______对对顶角.
14.如图所示,∠COE=90°,∠DOF=60°,OF平分∠AOC,求∠BOE的度数.
( http: / / )
◆开放探索创新
15.如图所示,(1)是某城市古建筑群中一座古塔底部的建筑平面图,请你利用学过的知识设计如何测量出古塔外墙底部的∠ABC大小的方案,并说明理由.注:(2),(3)图备用.
◆中考真题实战
16.(孝感)如图所示,OE是∠AOB的平分线,CD∥OB交OA于C,交OE于D,∠ACD=50°,则∠CDE的度数是( ).
A.125° B.130° D.140° D.155°
(第16题) (第17题) (第18题)
17.(龙岩)如图所示,l1∥l2,∠1与∠2的二倍,则∠3=_______.
18.(大连)如图所示,已知AB∥CD,∠1=∠2,若∠1=50°,则∠3=______.
19.(北京)如图所示,直线c与直线a,b相交,且a∥b,则下列结论中正确的个数为( ).
①∠1=∠2 ②∠1=∠3 ③∠3=∠2
A.0 B.1 C.2 D.3
( http: / / )
答案:
1.(1)∠BOC,∠AOD (2)∠DOE (3)∠AOC ∠BOD
2.B (点拨:因为构成∠1的两边与直线AB和EF有关,故∠1的邻补角有2个)
3.120° 90° 4.45°
5.(1)∠AOF (2)∠BOF (3)76° 6.135° 7.B
8.A (点拨:从一条边开始,不要遗漏)
9.60°
10.解:∠1和∠2不是对顶角,因为不是两条直线相交形成的角,∠1>∠2,因为可延长入射光线即得到∠1的对顶角∠3,而∠2在∠3的内部,故∠3>∠2,即∠1>∠2.
11.解:因为AB,CD相交于点O,所以∠AOD+∠AOC=180°,
又因为∠AOD-∠AOC=20°,所以∠AOD=∠AOC+20°,
所以2∠AOC+20°=180°,所以∠AOC=80°,
由对顶角相等,得∠BOD=80°.
又因为OE平分∠BOD,所以∠DOE=∠BOD=×80°=40°,
所以∠AOE=∠AOD+∠DOE=∠AOC+20°+40°=80°+20°+40°=140°.
12.解:根据对顶角相等,∠DOF=∠1=30°.
又因为∠AOD+∠DOF+∠2=180°,∠AOD=100°,
所以∠2=180°-∠AOD-∠DOF=180°-100°-30°=50°.
13.(1)2×1=2(对) (2)3×2=6(对)
(3)4×3=12(对) (4)n(n-1)=n2-n(对)
14.130°
15.解:把求∠ABC的大小转化到用古塔外墙的外部的角来求.
解法一:作AB的延长线,量出∠CBD的度数.
∠ABC=180°-∠CBD(邻补角的定义).
解法二:作AB和CB的延长线,量出∠DBE的度数就知道了∠ABC的度数(对顶角相等).
16.D 17.60° 18.80° 19.D
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
5.1.1 相交线
◆知能点分类训练
知能点1 邻补角的概念及性质
1.如图1所示,直线AB和CD相交于点O,OE是一条射线.
(1)写出∠AOC的邻补角:__________;(2)写出∠COE的邻补角:__________.
(3)写出与∠BOC邻补的角:________.
( http: / / )
(1) (2) (3)
2.如图2所示,三条直线AB,CE,EF相交于点O,则∠1的邻补角有( )个.
A.1 B.2 C.3 D.4
3.如图3所示,直线a,b,c两两相交,∠1=60°,∠2=∠4,则∠3=_____,∠5=__.
4.如图4所示,O为直线AB上一点,过O作一射线OC使∠AOC=3∠BOC,则∠BOC=_____.
(4) (5) (6)
知能点2 对顶角的概念及性质
5.如图5所示,直线AB,CD,EF相交于一点O.
(1)∠EOB的对顶角是________;(2)_______是∠AOE的对顶角;
(3)若∠AOC=76°,则∠BOD=________.
6.如图6所示,直线AB与CD相交于点O,若∠AOC+∠BOD=90°,则∠BOC=_____.
7.如图所示,∠1与∠2是对顶角的是( ).
( http: / / )
8.三条直线AB,CD,EF相交于同一点O,则图中对顶角有( ).
A.6对 B.5对 C.4对 D.3对
9.如图所示,直线AB和CD相交于点O,OE平分∠BOD,∠BOE=30°,那么∠COA=______.
◆规律方法应用
10.当光线射入水中,光线的传播方向发生改变,这就是折射现象.如图所示,插入水中的筷子变弯了,就是一种折射现象,图中的∠1和∠2是对顶角吗?比较∠1与∠2的大小关系并说明理由.
( http: / / )
11.如图所示,直线AB,CD相交于点O,OE平分∠BOD,∠AOD-∠AOC=20°,求∠AOE的度数.
12.直线AB,CD,EF相交于点O,且∠AOD=100°,∠1=30°,求∠2的度数.
13.(1)两条直线交于一点,有_____对对顶角.
(2)三条直线交于一点,有_______对对顶角.
(3)四条直线交于一点,有_______对对顶角.
(4)n条直线交于一点,有_______对对顶角.
14.如图所示,∠COE=90°,∠DOF=60°,OF平分∠AOC,求∠BOE的度数.
( http: / / )
◆开放探索创新
15.如图所示,(1)是某城市古建筑群中一座古塔底部的建筑平面图,请你利用学过的知识设计如何测量出古塔外墙底部的∠ABC大小的方案,并说明理由.注:(2),(3)图备用.
◆中考真题实战
16.(孝感)如图所示,OE是∠AOB的平分线,CD∥OB交OA于C,交OE于D,∠ACD=50°,则∠CDE的度数是( ).
A.125° B.130° D.140° D.155°
(第16题) (第17题) (第18题)
17.(龙岩)如图所示,l1∥l2,∠1与∠2的二倍,则∠3=_______.
18.(大连)如图所示,已知AB∥CD,∠1=∠2,若∠1=50°,则∠3=______.
19.(北京)如图所示,直线c与直线a,b相交,且a∥b,则下列结论中正确的个数为( ).
①∠1=∠2 ②∠1=∠3 ③∠3=∠2
A.0 B.1 C.2 D.3
( http: / / )
答案:
1.(1)∠BOC,∠AOD (2)∠DOE (3)∠AOC ∠BOD
2.B (点拨:因为构成∠1的两边与直线AB和EF有关,故∠1的邻补角有2个)
3.120° 90° 4.45°
5.(1)∠AOF (2)∠BOF (3)76° 6.135° 7.B
8.A (点拨:从一条边开始,不要遗漏)
9.60°
10.解:∠1和∠2不是对顶角,因为不是两条直线相交形成的角,∠1>∠2,因为可延长入射光线即得到∠1的对顶角∠3,而∠2在∠3的内部,故∠3>∠2,即∠1>∠2.
11.解:因为AB,CD相交于点O,所以∠AOD+∠AOC=180°,
又因为∠AOD-∠AOC=20°,所以∠AOD=∠AOC+20°,
所以2∠AOC+20°=180°,所以∠AOC=80°,
由对顶角相等,得∠BOD=80°.
又因为OE平分∠BOD,所以∠DOE=∠BOD=×80°=40°,
所以∠AOE=∠AOD+∠DOE=∠AOC+20°+40°=80°+20°+40°=140°.
12.解:根据对顶角相等,∠DOF=∠1=30°.
又因为∠AOD+∠DOF+∠2=180°,∠AOD=100°,
所以∠2=180°-∠AOD-∠DOF=180°-100°-30°=50°.
13.(1)2×1=2(对) (2)3×2=6(对)
(3)4×3=12(对) (4)n(n-1)=n2-n(对)
14.130°
15.解:把求∠ABC的大小转化到用古塔外墙的外部的角来求.
解法一:作AB的延长线,量出∠CBD的度数.
∠ABC=180°-∠CBD(邻补角的定义).
解法二:作AB和CB的延长线,量出∠DBE的度数就知道了∠ABC的度数(对顶角相等).
16.D 17.60° 18.80° 19.D
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
