九年级下数学: 函数与方程 综合应用 课件ppt(共15张ppt)
文档属性
| 名称 | 九年级下数学: 函数与方程 综合应用 课件ppt(共15张ppt) |

|
|
| 格式 | rar | ||
| 文件大小 | 818.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-01-27 00:00:00 | ||
图片预览





文档简介
课件15张PPT。九年级下数学: 函数与方程 综合应用 课件ppt高邮市赞化学校函数与方程
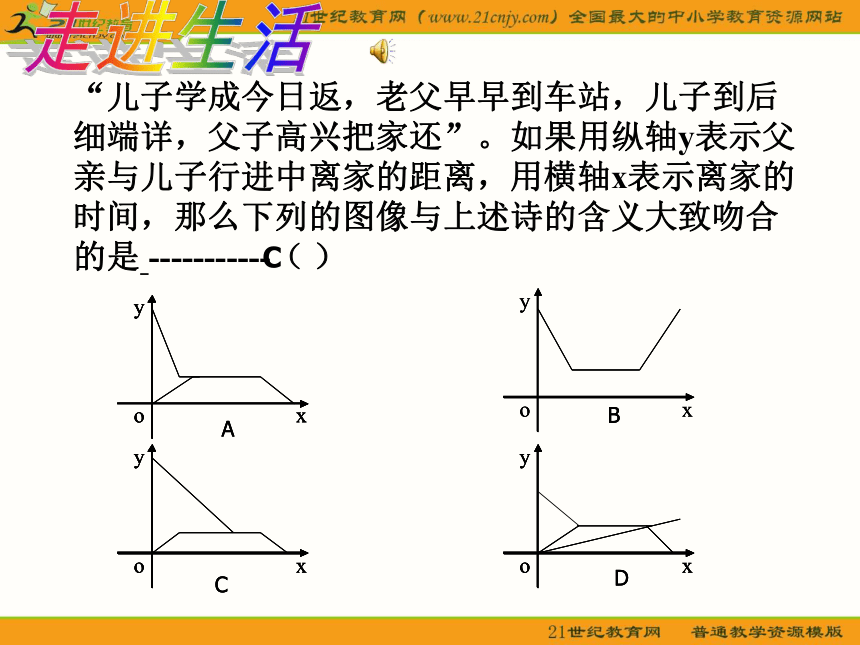
综合应用2007届九年级数学复习专题(一) 走进课标“儿子学成今日返,老父早早到车站,儿子到后细端详,父子高兴把家还”。如果用纵轴y表示父亲与儿子行进中离家的距离,用横轴x表示离家的时间,那么下列的图像与上述诗的含义大致吻合的是 -----------( ) 走进生活C 教室里放有一台饮水机(如图),饮水机上有两个放水管.课间同学们依次到饮水机前用茶杯接水.假设接水过程中水不发生泼洒,每个同学所接的水量都是相等的.两个放水管同时打开时,他们的流量相同.放水时先打开一个水管,过一会儿,再打开第二个水管,放水过程中阀门一直开着.饮水机的存水量y(升)与放水时间x(分钟)的函数关系如图所示:⑴求出饮水机的存水量y(升)与放水时间x
(分钟)(x≥2)的函数关系式;
⑵如果打开第一个水管后,2分钟时恰
好有4个同学接水结束,则前22个同
学接水结束共需要几分钟?
⑶按(2)的放法,求出在课间10分
钟内班级中最多有多少个同学能及时接完水?考查内容:结合函数图象特征分析函数关系,要求既会挖掘未知的关系,又能进行合理推断。 某商店经销成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克;销售价每涨1元,月销售量就减少10千克。针对这种水产品的销售情况,请解答以下问题:
(1)设销售单价为每千克x元,月销售利润为y元,求y与x的函数关系式(不必写出x的取值范围);
(2)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?走进社会解:
(1)y=(x-40)[500-10(x-50)]
=(X-40)(100-10x)
=-10x2+1400x-40000
(2)当y=8000时,得
-10x2+1400x-40000=8000
10x2 -1400x+48000=0
解得 x1=60,x2=80。
当x1=60时,成本为400 40=16000
当x2=80时,成本为200 40=8000。
故销售单价定为每千克80元。一慢车和一快车沿相同的路线从A地到B地所行的路程与时间的函数图象,回答下列问题:
(1)慢车比快车早出发_____小时,快车追上慢车时行驶了__千米,快车比慢车早__小时到达B地
(2)在下列3个问题中选一题
快车追上慢车需几小时?
求慢车,快车的速度.
求AB两地之间的路程考考你22764走进竞技场 台球是一项高雅的体育运动,其中包含了许多物理学、几何学知识,图(1)是一个台球桌,目标球F与目标球E之间有一个G球阻挡.
(1)击球者想通过击打E球,让E球先撞击球台的AB,经过一次反弹后再撞击F球,他应将E球打到AB边上的哪一点?请在图(1)中用尺规作出这一点H,并作出E球的运行路线;
(2)如图(2),现以D为原点,建立直角坐标系,记A(0,4),C(8,0),E(4,3),F(7,1),求E球按刚才方式运行到F球的路线长度及H点的坐标。(忽略球的大小)DCBAEGFHF,MA(0,4),C(8,0),E(4,3),F(7,1) 函数思想,就是用运动、变化的观点,分析研究具体问题中的数量关系,通过函数的形式,把这种数量关系表示出来并加以研究,从而使问题获得解决。
方程思想,就是在解决某些数学问题时,先设定一些未知数,然后把它们当做已知数,根据题设本身总量间的制约,列出等式,所设未知数沟通了变量之间的关系的一种思想方法。
函数与方程是两个不同的概念,但它们之间有着密切的联系,一个函数若有解析表达式,那么这个表达式就可以看成是一个方程。因此,许多有关方程的问题可用函数的方法解决;反之,许多有关函数的问题也可以用方程的方法解决。学会学习谢谢指导!
综合应用2007届九年级数学复习专题(一) 走进课标“儿子学成今日返,老父早早到车站,儿子到后细端详,父子高兴把家还”。如果用纵轴y表示父亲与儿子行进中离家的距离,用横轴x表示离家的时间,那么下列的图像与上述诗的含义大致吻合的是 -----------( ) 走进生活C 教室里放有一台饮水机(如图),饮水机上有两个放水管.课间同学们依次到饮水机前用茶杯接水.假设接水过程中水不发生泼洒,每个同学所接的水量都是相等的.两个放水管同时打开时,他们的流量相同.放水时先打开一个水管,过一会儿,再打开第二个水管,放水过程中阀门一直开着.饮水机的存水量y(升)与放水时间x(分钟)的函数关系如图所示:⑴求出饮水机的存水量y(升)与放水时间x
(分钟)(x≥2)的函数关系式;
⑵如果打开第一个水管后,2分钟时恰
好有4个同学接水结束,则前22个同
学接水结束共需要几分钟?
⑶按(2)的放法,求出在课间10分
钟内班级中最多有多少个同学能及时接完水?考查内容:结合函数图象特征分析函数关系,要求既会挖掘未知的关系,又能进行合理推断。 某商店经销成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克;销售价每涨1元,月销售量就减少10千克。针对这种水产品的销售情况,请解答以下问题:
(1)设销售单价为每千克x元,月销售利润为y元,求y与x的函数关系式(不必写出x的取值范围);
(2)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?走进社会解:
(1)y=(x-40)[500-10(x-50)]
=(X-40)(100-10x)
=-10x2+1400x-40000
(2)当y=8000时,得
-10x2+1400x-40000=8000
10x2 -1400x+48000=0
解得 x1=60,x2=80。
当x1=60时,成本为400 40=16000
当x2=80时,成本为200 40=8000。
故销售单价定为每千克80元。一慢车和一快车沿相同的路线从A地到B地所行的路程与时间的函数图象,回答下列问题:
(1)慢车比快车早出发_____小时,快车追上慢车时行驶了__千米,快车比慢车早__小时到达B地
(2)在下列3个问题中选一题
快车追上慢车需几小时?
求慢车,快车的速度.
求AB两地之间的路程考考你22764走进竞技场 台球是一项高雅的体育运动,其中包含了许多物理学、几何学知识,图(1)是一个台球桌,目标球F与目标球E之间有一个G球阻挡.
(1)击球者想通过击打E球,让E球先撞击球台的AB,经过一次反弹后再撞击F球,他应将E球打到AB边上的哪一点?请在图(1)中用尺规作出这一点H,并作出E球的运行路线;
(2)如图(2),现以D为原点,建立直角坐标系,记A(0,4),C(8,0),E(4,3),F(7,1),求E球按刚才方式运行到F球的路线长度及H点的坐标。(忽略球的大小)DCBAEGFHF,MA(0,4),C(8,0),E(4,3),F(7,1) 函数思想,就是用运动、变化的观点,分析研究具体问题中的数量关系,通过函数的形式,把这种数量关系表示出来并加以研究,从而使问题获得解决。
方程思想,就是在解决某些数学问题时,先设定一些未知数,然后把它们当做已知数,根据题设本身总量间的制约,列出等式,所设未知数沟通了变量之间的关系的一种思想方法。
函数与方程是两个不同的概念,但它们之间有着密切的联系,一个函数若有解析表达式,那么这个表达式就可以看成是一个方程。因此,许多有关方程的问题可用函数的方法解决;反之,许多有关函数的问题也可以用方程的方法解决。学会学习谢谢指导!
