5.3.2 命题、定理(含答案)
文档属性
| 名称 | 5.3.2 命题、定理(含答案) |

|
|
| 格式 | rar | ||
| 文件大小 | 93.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-01-27 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
5.3.2 命题、定理
◆知能点分类训练
知能点1 命题的概念及命题的组成
1.下列语句是命题的个数为( ).
①画∠AOB的平分线; ②直角都相等; ③同旁内角互补吗? ④若│a│=3,则a=3.
A.1个 B.2个 C.3个 D.4个
2.下列5个命题,其中真命题的个数为( ).
①两个锐角之和一定是钝角; ②直角小于夹角; ③同位角相等,两直线平行;
④内错角互补,两直线平行; ⑤如果aA.1个 B.2个 C.3个 D.4个
3.下列说法正确的是( ).
A.互补的两个角是邻补角; B.两直线平行,同旁内角相等;
C.“同旁内角互补”不是命题; D.“相等的两个角是对顶角”是假命题
4.“同一平面内,垂直于同一条直线的两条直线互相平行”是______命题,题设是_____________,改写成“如果……那么……”的形式是______________________.
5.判断下列命题是真命题还是假命题,若是假命题,请举出一个反例.
(1)钝角与锐角的差为锐角;____________________________________________.
(2)若a>b,则ac2>bc2;_______________________________________________.
(3)内错角相等._______________________________________________________.
6.将下列命题改写成“如果……那么……”的形式.
(1)直角都相等.
(2)末位数是5的整数能被5整除.
(3)三角形的内角和是180°.
(4)平行于同一条直线的两条直线互相平行.
规律方法应用
7.如图所示,已知∠B=43°,∠BDC=43°,∠A=∠1,试说明∠4=∠BDE.
8.如图所示,AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=( ).
A.180° B.270° C.360° D.540°
9.从一只船上测得灯塔的方向为南偏东30°,那么从灯塔上测得船的方向是什么?(要求:画出图形,并说明理由)
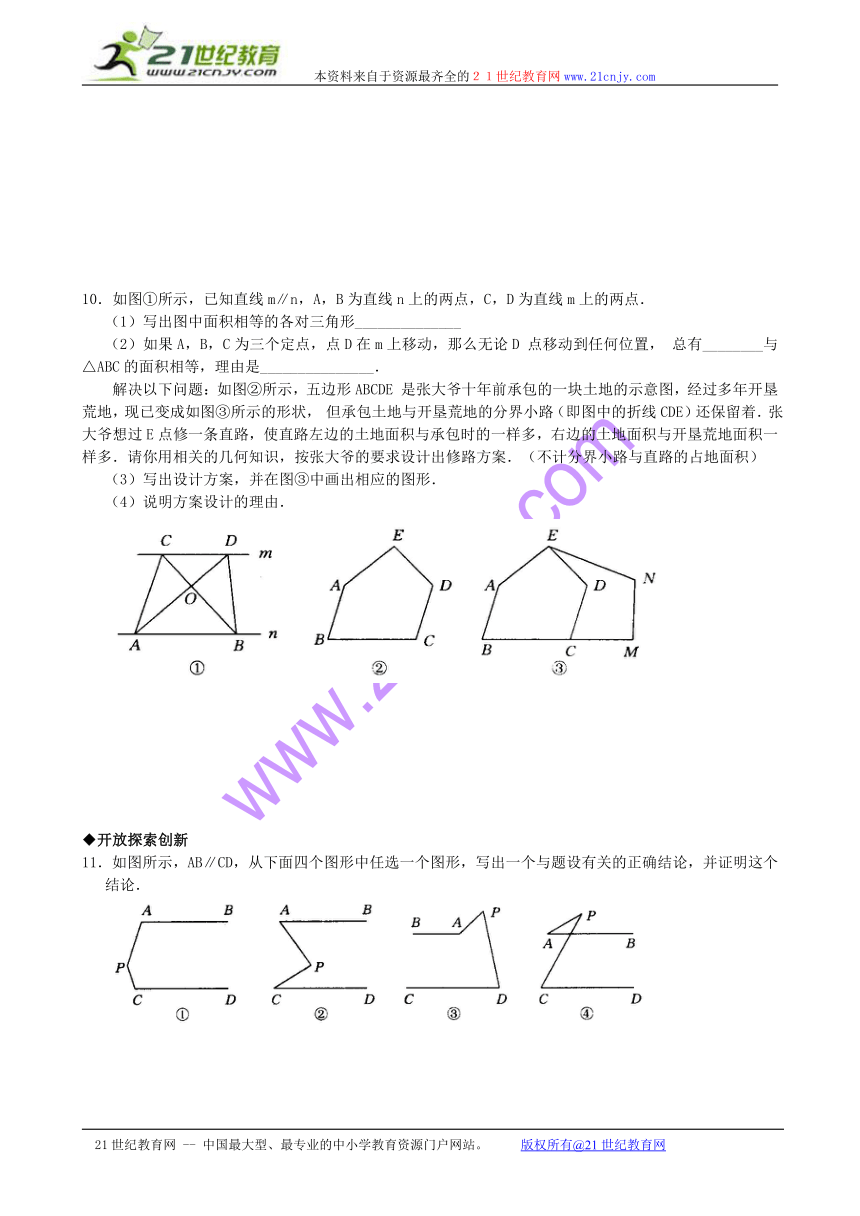
10.如图①所示,已知直线m∥n,A,B为直线n上的两点,C,D为直线m上的两点.
(1)写出图中面积相等的各对三角形______________
(2)如果A,B,C为三个定点,点D在m上移动,那么无论D点移动到任何位置,总有________与△ABC的面积相等,理由是_______________.
解决以下问题:如图②所示,五边形ABCDE是张大爷十年前承包的一块土地的示意图,经过多年开垦荒地,现已变成如图③所示的形状,但承包土地与开垦荒地的分界小路(即图中的折线CDE)还保留着.张大爷想过E点修一条直路,使直路左边的土地面积与承包时的一样多,右边的土地面积与开垦荒地面积一样多.请你用相关的几何知识,按张大爷的要求设计出修路方案.(不计分界小路与直路的占地面积)
(3)写出设计方案,并在图③中画出相应的图形.
(4)说明方案设计的理由.
◆开放探索创新
11.如图所示,AB∥CD,从下面四个图形中任选一个图形,写出一个与题设有关的正确结论,并证明这个结论.
( http: / / )
◆中考真题实战
12.(湖南)下列命题正确的是( ).
①若∠1+∠2=90°,则∠1与∠2互为余角
②若∠A+∠B=180°,则∠A与∠B互为邻补角
③120°的角和60°的角都是补角
④同角的余角相等
⑤由两条射线组成的图形叫做角
A.①③ B.②⑤ C.③④ D.①④
答案:
1.B (点拨:②④是命题)
2.C (点拨:②③⑤正确)
3.D
4.真 在同一平面内,两条直线同垂直于一条直线,这两条直线互相平行; 在同一平面内,如果两条直线同垂直于一条直线,那么这两条直线互相平行
5.(1)假命题,例如∠α=120°,∠β=20°
(2)假命题,例如a=10,b=1,c=0
(3)假命题,例如:∠1≠∠2
6.(1)如果几个角是直角,那么它们都相等.
(2)如果一个整数的末位数是5,那么它能被5整除.
(3)如果一个图形是三角形,那么它的内角和是180°.
(4)如果两条直线都和第三条直线平行,那么这两条直线互相平行
7.证明:∵∠B=43°,∠BDC=43°,
∴∠B=∠BDC,
∴AB∥CD(内错角相等,两直线平行),
∴∠A=∠C(两直线平行,内错角相等).
∵∠A=∠1,∴∠C=∠1,
∴AC∥DE(内错角相等,两直线平行),
∴∠4=∠BDE(两直线平行,内错角相等).
8.C
9.如答图所示.由图中可知AD∥BC,
( http: / / )
∴∠EAB=∠ABC=30°,
∴由灯塔测得船的方向为北偏西30°,
船在A点,灯塔在B点.
10.(1)△ABC和△ABD,△AOC和△BOD,△CDA和△CDB.
(2)△ABD 平行线间的距离处处相等,所以无论点D在m上移动到何位置,总有△ABD与△ABC同底等高,因此它们的面积相等.
(3)如答图所示,连结EC,过D作DF∥EC交CM于点F,连结EF,则EF即为所求直线.
(4)设EF交CD于点H,由(1),(2)知S△ECF=S△ECD,所以S△ECF -S△ECH=S△ECD-S△ECH,
所以S△HCF =S△EDH,
所以S五边形ABCDE=S四边形ABFE,S五边形EDCMN=S四边形EFMN.
11.本题开放,提供一种解法.
解:图②的结论可以是:∠P=∠A+∠C.
( http: / / )
证明:过P作PE∥AB,则∠A=∠APE.
∵AB∥CD,∴PE∥CD,
∴∠EPC=∠C,
∴∠APE+∠EPC=∠A+∠C,
即∠APC=∠A+∠C.
12.D
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
5.3.2 命题、定理
◆知能点分类训练
知能点1 命题的概念及命题的组成
1.下列语句是命题的个数为( ).
①画∠AOB的平分线; ②直角都相等; ③同旁内角互补吗? ④若│a│=3,则a=3.
A.1个 B.2个 C.3个 D.4个
2.下列5个命题,其中真命题的个数为( ).
①两个锐角之和一定是钝角; ②直角小于夹角; ③同位角相等,两直线平行;
④内错角互补,两直线平行; ⑤如果a
3.下列说法正确的是( ).
A.互补的两个角是邻补角; B.两直线平行,同旁内角相等;
C.“同旁内角互补”不是命题; D.“相等的两个角是对顶角”是假命题
4.“同一平面内,垂直于同一条直线的两条直线互相平行”是______命题,题设是_____________,改写成“如果……那么……”的形式是______________________.
5.判断下列命题是真命题还是假命题,若是假命题,请举出一个反例.
(1)钝角与锐角的差为锐角;____________________________________________.
(2)若a>b,则ac2>bc2;_______________________________________________.
(3)内错角相等._______________________________________________________.
6.将下列命题改写成“如果……那么……”的形式.
(1)直角都相等.
(2)末位数是5的整数能被5整除.
(3)三角形的内角和是180°.
(4)平行于同一条直线的两条直线互相平行.
规律方法应用
7.如图所示,已知∠B=43°,∠BDC=43°,∠A=∠1,试说明∠4=∠BDE.
8.如图所示,AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=( ).
A.180° B.270° C.360° D.540°
9.从一只船上测得灯塔的方向为南偏东30°,那么从灯塔上测得船的方向是什么?(要求:画出图形,并说明理由)
10.如图①所示,已知直线m∥n,A,B为直线n上的两点,C,D为直线m上的两点.
(1)写出图中面积相等的各对三角形______________
(2)如果A,B,C为三个定点,点D在m上移动,那么无论D点移动到任何位置,总有________与△ABC的面积相等,理由是_______________.
解决以下问题:如图②所示,五边形ABCDE是张大爷十年前承包的一块土地的示意图,经过多年开垦荒地,现已变成如图③所示的形状,但承包土地与开垦荒地的分界小路(即图中的折线CDE)还保留着.张大爷想过E点修一条直路,使直路左边的土地面积与承包时的一样多,右边的土地面积与开垦荒地面积一样多.请你用相关的几何知识,按张大爷的要求设计出修路方案.(不计分界小路与直路的占地面积)
(3)写出设计方案,并在图③中画出相应的图形.
(4)说明方案设计的理由.
◆开放探索创新
11.如图所示,AB∥CD,从下面四个图形中任选一个图形,写出一个与题设有关的正确结论,并证明这个结论.
( http: / / )
◆中考真题实战
12.(湖南)下列命题正确的是( ).
①若∠1+∠2=90°,则∠1与∠2互为余角
②若∠A+∠B=180°,则∠A与∠B互为邻补角
③120°的角和60°的角都是补角
④同角的余角相等
⑤由两条射线组成的图形叫做角
A.①③ B.②⑤ C.③④ D.①④
答案:
1.B (点拨:②④是命题)
2.C (点拨:②③⑤正确)
3.D
4.真 在同一平面内,两条直线同垂直于一条直线,这两条直线互相平行; 在同一平面内,如果两条直线同垂直于一条直线,那么这两条直线互相平行
5.(1)假命题,例如∠α=120°,∠β=20°
(2)假命题,例如a=10,b=1,c=0
(3)假命题,例如:∠1≠∠2
6.(1)如果几个角是直角,那么它们都相等.
(2)如果一个整数的末位数是5,那么它能被5整除.
(3)如果一个图形是三角形,那么它的内角和是180°.
(4)如果两条直线都和第三条直线平行,那么这两条直线互相平行
7.证明:∵∠B=43°,∠BDC=43°,
∴∠B=∠BDC,
∴AB∥CD(内错角相等,两直线平行),
∴∠A=∠C(两直线平行,内错角相等).
∵∠A=∠1,∴∠C=∠1,
∴AC∥DE(内错角相等,两直线平行),
∴∠4=∠BDE(两直线平行,内错角相等).
8.C
9.如答图所示.由图中可知AD∥BC,
( http: / / )
∴∠EAB=∠ABC=30°,
∴由灯塔测得船的方向为北偏西30°,
船在A点,灯塔在B点.
10.(1)△ABC和△ABD,△AOC和△BOD,△CDA和△CDB.
(2)△ABD 平行线间的距离处处相等,所以无论点D在m上移动到何位置,总有△ABD与△ABC同底等高,因此它们的面积相等.
(3)如答图所示,连结EC,过D作DF∥EC交CM于点F,连结EF,则EF即为所求直线.
(4)设EF交CD于点H,由(1),(2)知S△ECF=S△ECD,所以S△ECF -S△ECH=S△ECD-S△ECH,
所以S△HCF =S△EDH,
所以S五边形ABCDE=S四边形ABFE,S五边形EDCMN=S四边形EFMN.
11.本题开放,提供一种解法.
解:图②的结论可以是:∠P=∠A+∠C.
( http: / / )
证明:过P作PE∥AB,则∠A=∠APE.
∵AB∥CD,∴PE∥CD,
∴∠EPC=∠C,
∴∠APE+∠EPC=∠A+∠C,
即∠APC=∠A+∠C.
12.D
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
