淮南市2011届高三第一次质检(数学文)
文档属性
| 名称 | 淮南市2011届高三第一次质检(数学文) |
|
|
| 格式 | zip | ||
| 文件大小 | 188.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-02-08 19:53:00 | ||
图片预览




文档简介
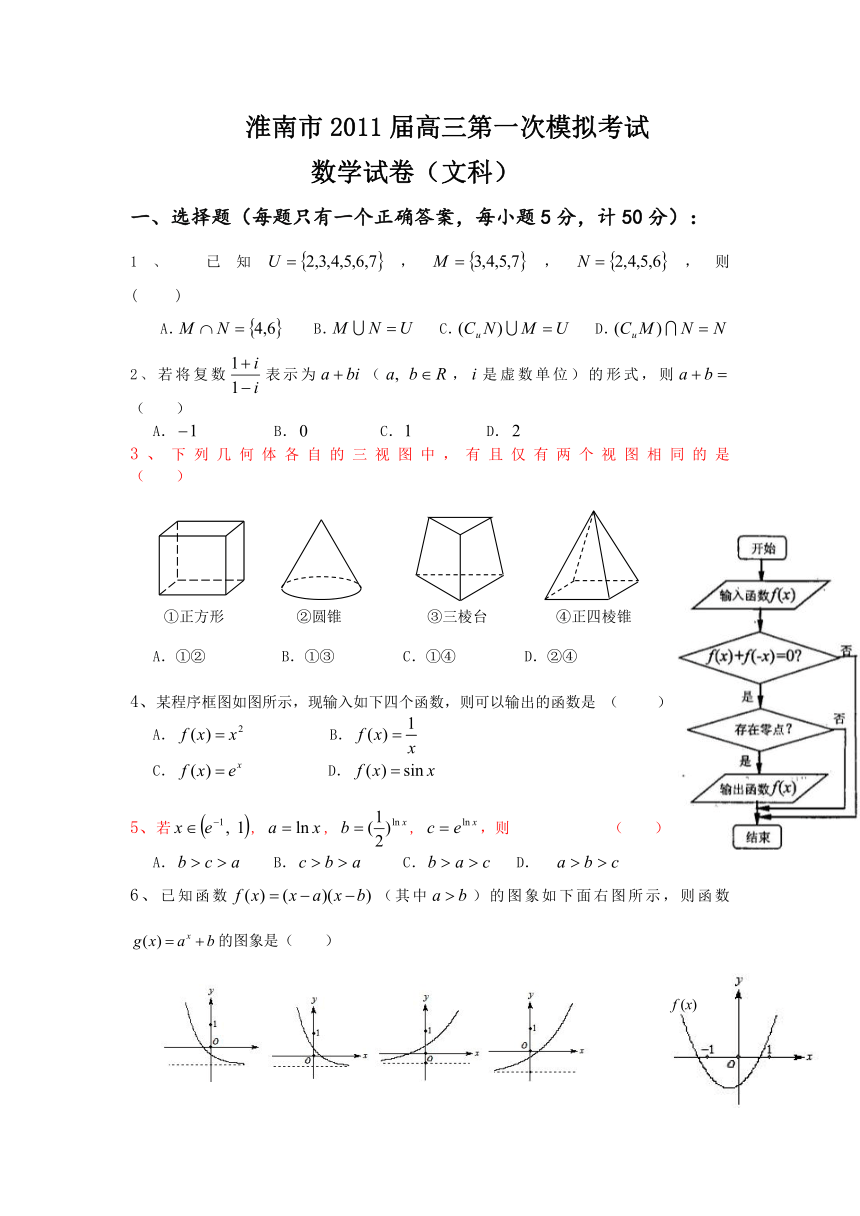
淮南市2011届高三第一次模拟考试
数学试卷(文科)
一、选择题(每题只有一个正确答案,每小题5分,计50分):
1、 已知,,,则 ( )
A. B. C. D.
2、若将复数表示为(,是虚数单位)的形式,则 ( )
A. B. C. D.
3、下列几何体各自的三视图中,有且仅有两个视图相同的是 ( )
A.①② B.①③ C.①④ D.②④
4、某程序框图如图所示,现输入如下四个函数,则可以输出的函数是 ( )
A. B.
C. D.
5、若, , , ,则 ( )
A. B. C. D.
6、已知函数(其中)的图象如下面右图所示,则函数的图象是( )
A. B. C. D.
7、 抛物线的准线与双曲线的右准线重合,则的值是 ( )
A. B. C. D.
8、若实数x,y满足不等式组:,则该约束条件所围成的平面区域的面积是( )
A.3 B. C.2 D.
9、给出命题:
(1)在空间里,垂直于同一平面的两个平面平行;
(2)设是不同的直线,是一个平面,若,∥,则;
(3)已知表示两个不同平面,为平面内的一条直线,则“”是“”的充要条件;
(4)是两条异面直线,为空间一点, 过总可以作一个平面与之一垂直,与另一个平行。
其中正确命题个数是 ( )
A.0 B.1 C.2 D.3
10、已知直线及与函数图像的交点分别为,与函数图像的交点分别为
、,则直线与 ( )
A. 相交,且交点在第I象限 B. 相交,且交点在第II象限
C. 相交,且交点在第IV象限 D. 相交,且交点在坐标原点
二、填空题(每小题5分,计25分):
11、设是第三象限角,,则 ;
12、已知定义在上的函数满足:,若,则 ;
13、已知数列{an}的前n项和,则= ;
14、 已知点是的重心,( , ),若,,则的最小值是 ;
15、已知函数(是常数且).对于下列命题:
①函数f(x)的最小值是-1;②函数f(x)在R上是单调函数;③若在上恒成立,则的取值范围是;④对任意且,恒有.
其中正确命题的序号是 .
三、解答题(共计6题,计75分):
16、(本小题12分)已知函数.
(Ⅰ)已知:,求函数单调减区间;
(Ⅱ)若函数按向量平移后得到函数,且函数,求向量。
17、(本小题12分)某中学的高二(1)班男同学有名,女同学有名,老师按照分层抽样的方法组建了一个人的课外兴趣小组.
(Ⅰ)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(Ⅱ)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
(Ⅲ)试验结束后,第一次做试验的同学得到的试验数据为,第二次做试验的同学得到的试验数据为,请问哪位同学的实验更稳定?并说明理由.
18、(本小题12分)如图是以正方形为底面的正四棱柱被一平面所截得的几何体,四边形为截面,且,,,
(Ⅰ)证明:截面四边形是菱形;
(Ⅱ)求几何体的体积.
19、(本小题13分)已知函数,
(Ⅰ)求函数的单调区间;
(Ⅱ)在区间内存在,使不等式成立,求的取值范围。
20、(本小题13分)已知等比数列满足:,且是,的等差中项。
(Ⅰ)求数列的通项公式;
(Ⅱ)若,,求 成立的正整数的最小值。
21、(本题13分)已知椭圆的方程是,点分别是椭圆的长轴的左、右端点,
左焦点坐标为,且过点。
(Ⅰ)求椭圆的方程;
(Ⅱ)已知是椭圆的右焦点,以为直径的圆记为圆,试问:过点能否引圆的切线,若能,求出这条切线与轴及圆的弦所对的劣弧围成的图形的面积;若不能,说明理由。
2011届淮南市第一次模拟考试
数学(文科)试卷(参考答案)
一、 1-5 BCDDA; 6-10 ABCBD
二、 11、; 12、; 13、350; 14、 ; 15、①③④
三、解答题:
16、(本小题满分12分)
解:(1)
=. …………………2分
,,
当时,; 当时,,
又,;
所以,函数单调减区间为:和 …………………6分
(2),
,所以,向量……………12分
17、(本小题满分12分)
解:(Ⅰ)某同学被抽到的概率为………………2分
设有名男同学,则,男、女同学的人数分别为………………4分
(Ⅱ)把名男同学和名女同学记为,则选取两名同学的基本事件有共种,其中有一名女同学的有种
选出的两名同学中恰有一名女同学的概率为……………………………8分
(Ⅲ),
,
第二同学的实验更稳定………………………12分
18、(本小题满分12分)
解:(Ⅰ)证明:因为平面∥平面,且平面分别交
平面、平面于直线、,所以∥.
同理,∥.
因此,四边形为平行四边形. ……(1)
因为,而为在底面上的射影,所以.
因为,所以∥.
因此,. ……(2)
由(1)、(2)可知:四边形是菱形;…………………6分
(Ⅱ)连结、、、,则
,,且几何体是以正方形为底面的正四棱柱的一部分,
该几何体的体积为,
同理,得
所以,,
即几何体的体积为2. …………………12分
19、(本小题满分13分)
解:(Ⅰ)函数的定义域为,
当,即时,为单调递增函数;
当,即时,为单调递减函数;
所以,的单调递增区间是,的单调递减区间是…………6分
(Ⅱ)由不等式,得,令,则
由题意可转化为:在区间内,,
,令,得
- 0 +
递减 极小值 递增
由表可知:的极小值是且唯一,
所以。 因此,所求的取值范围是。…………12分
20、(本小题满分13分)
解:(Ⅰ)设等比数列的首项为,公比为,
依题意,有
由 及,得 ,或
当时,式不成立;当时,符合题意 ┉┉┉┉┉4分
把代入(2)得,所以, ┉┉┉┉┉6分
(Ⅱ) ┉┉┉┉┉┉┉┉7分
(3)-(4)得
┉┉┉┉┉10分
,即,
又当时,
当时, ┉┉┉┉┉┉┉┉12分
故使成立的正整数的最小值为5 . ┉┉┉┉┉┉┉┉13分
21、(本小题满分13分)
解:(Ⅰ)因为椭圆的方程为,(), ∴ ,
即椭圆的方程为, ∵ 点在椭圆上, ∴ ,
解得 或(舍), 由此得,
所以,所求椭圆的标准方程为. …… 6分
(Ⅱ)由(Ⅰ)知,,又,则得,
所以,即, 是, 所以,以为直径的圆必过点,因此,过 点能引出该圆的切线,设切线为,交轴于点, 又的中点为,则显然,
而 , 所以的斜率为,
因此,过 点引圆的切线方程为:, 即
令,则,,又,
所以,
因此,所求的图形面积是 =
…… 13分
①正方形
②圆锥
③三棱台
④正四棱锥
f (x)
A
B
F
y
x
P
OO
A M O F Q x
y
P
数学试卷(文科)
一、选择题(每题只有一个正确答案,每小题5分,计50分):
1、 已知,,,则 ( )
A. B. C. D.
2、若将复数表示为(,是虚数单位)的形式,则 ( )
A. B. C. D.
3、下列几何体各自的三视图中,有且仅有两个视图相同的是 ( )
A.①② B.①③ C.①④ D.②④
4、某程序框图如图所示,现输入如下四个函数,则可以输出的函数是 ( )
A. B.
C. D.
5、若, , , ,则 ( )
A. B. C. D.
6、已知函数(其中)的图象如下面右图所示,则函数的图象是( )
A. B. C. D.
7、 抛物线的准线与双曲线的右准线重合,则的值是 ( )
A. B. C. D.
8、若实数x,y满足不等式组:,则该约束条件所围成的平面区域的面积是( )
A.3 B. C.2 D.
9、给出命题:
(1)在空间里,垂直于同一平面的两个平面平行;
(2)设是不同的直线,是一个平面,若,∥,则;
(3)已知表示两个不同平面,为平面内的一条直线,则“”是“”的充要条件;
(4)是两条异面直线,为空间一点, 过总可以作一个平面与之一垂直,与另一个平行。
其中正确命题个数是 ( )
A.0 B.1 C.2 D.3
10、已知直线及与函数图像的交点分别为,与函数图像的交点分别为
、,则直线与 ( )
A. 相交,且交点在第I象限 B. 相交,且交点在第II象限
C. 相交,且交点在第IV象限 D. 相交,且交点在坐标原点
二、填空题(每小题5分,计25分):
11、设是第三象限角,,则 ;
12、已知定义在上的函数满足:,若,则 ;
13、已知数列{an}的前n项和,则= ;
14、 已知点是的重心,( , ),若,,则的最小值是 ;
15、已知函数(是常数且).对于下列命题:
①函数f(x)的最小值是-1;②函数f(x)在R上是单调函数;③若在上恒成立,则的取值范围是;④对任意且,恒有.
其中正确命题的序号是 .
三、解答题(共计6题,计75分):
16、(本小题12分)已知函数.
(Ⅰ)已知:,求函数单调减区间;
(Ⅱ)若函数按向量平移后得到函数,且函数,求向量。
17、(本小题12分)某中学的高二(1)班男同学有名,女同学有名,老师按照分层抽样的方法组建了一个人的课外兴趣小组.
(Ⅰ)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(Ⅱ)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
(Ⅲ)试验结束后,第一次做试验的同学得到的试验数据为,第二次做试验的同学得到的试验数据为,请问哪位同学的实验更稳定?并说明理由.
18、(本小题12分)如图是以正方形为底面的正四棱柱被一平面所截得的几何体,四边形为截面,且,,,
(Ⅰ)证明:截面四边形是菱形;
(Ⅱ)求几何体的体积.
19、(本小题13分)已知函数,
(Ⅰ)求函数的单调区间;
(Ⅱ)在区间内存在,使不等式成立,求的取值范围。
20、(本小题13分)已知等比数列满足:,且是,的等差中项。
(Ⅰ)求数列的通项公式;
(Ⅱ)若,,求 成立的正整数的最小值。
21、(本题13分)已知椭圆的方程是,点分别是椭圆的长轴的左、右端点,
左焦点坐标为,且过点。
(Ⅰ)求椭圆的方程;
(Ⅱ)已知是椭圆的右焦点,以为直径的圆记为圆,试问:过点能否引圆的切线,若能,求出这条切线与轴及圆的弦所对的劣弧围成的图形的面积;若不能,说明理由。
2011届淮南市第一次模拟考试
数学(文科)试卷(参考答案)
一、 1-5 BCDDA; 6-10 ABCBD
二、 11、; 12、; 13、350; 14、 ; 15、①③④
三、解答题:
16、(本小题满分12分)
解:(1)
=. …………………2分
,,
当时,; 当时,,
又,;
所以,函数单调减区间为:和 …………………6分
(2),
,所以,向量……………12分
17、(本小题满分12分)
解:(Ⅰ)某同学被抽到的概率为………………2分
设有名男同学,则,男、女同学的人数分别为………………4分
(Ⅱ)把名男同学和名女同学记为,则选取两名同学的基本事件有共种,其中有一名女同学的有种
选出的两名同学中恰有一名女同学的概率为……………………………8分
(Ⅲ),
,
第二同学的实验更稳定………………………12分
18、(本小题满分12分)
解:(Ⅰ)证明:因为平面∥平面,且平面分别交
平面、平面于直线、,所以∥.
同理,∥.
因此,四边形为平行四边形. ……(1)
因为,而为在底面上的射影,所以.
因为,所以∥.
因此,. ……(2)
由(1)、(2)可知:四边形是菱形;…………………6分
(Ⅱ)连结、、、,则
,,且几何体是以正方形为底面的正四棱柱的一部分,
该几何体的体积为,
同理,得
所以,,
即几何体的体积为2. …………………12分
19、(本小题满分13分)
解:(Ⅰ)函数的定义域为,
当,即时,为单调递增函数;
当,即时,为单调递减函数;
所以,的单调递增区间是,的单调递减区间是…………6分
(Ⅱ)由不等式,得,令,则
由题意可转化为:在区间内,,
,令,得
- 0 +
递减 极小值 递增
由表可知:的极小值是且唯一,
所以。 因此,所求的取值范围是。…………12分
20、(本小题满分13分)
解:(Ⅰ)设等比数列的首项为,公比为,
依题意,有
由 及,得 ,或
当时,式不成立;当时,符合题意 ┉┉┉┉┉4分
把代入(2)得,所以, ┉┉┉┉┉6分
(Ⅱ) ┉┉┉┉┉┉┉┉7分
(3)-(4)得
┉┉┉┉┉10分
,即,
又当时,
当时, ┉┉┉┉┉┉┉┉12分
故使成立的正整数的最小值为5 . ┉┉┉┉┉┉┉┉13分
21、(本小题满分13分)
解:(Ⅰ)因为椭圆的方程为,(), ∴ ,
即椭圆的方程为, ∵ 点在椭圆上, ∴ ,
解得 或(舍), 由此得,
所以,所求椭圆的标准方程为. …… 6分
(Ⅱ)由(Ⅰ)知,,又,则得,
所以,即, 是, 所以,以为直径的圆必过点,因此,过 点能引出该圆的切线,设切线为,交轴于点, 又的中点为,则显然,
而 , 所以的斜率为,
因此,过 点引圆的切线方程为:, 即
令,则,,又,
所以,
因此,所求的图形面积是 =
…… 13分
①正方形
②圆锥
③三棱台
④正四棱锥
f (x)
A
B
F
y
x
P
OO
A M O F Q x
y
P
同课章节目录
