1.1.2集合间的基本关系课件
文档属性
| 名称 | 1.1.2集合间的基本关系课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 216.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-02-13 00:00:00 | ||
图片预览







文档简介
课件25张PPT。1.1.2 集合间的基本关系复习元素与集合的关系——属于与不属于的关系,填以下空白:
(1)0 N;(2) Q;(3)-1.5 R
(2)类比实数的大小关系,如5<7,2≤2,试想集合间是否有类似的“大小”关系呢?(4)C={x|x是三条边相等的三角形}
D={x|X是三个内角相等的三角形}他们的关系是:
(1),(2),(3)中集合A中的每一个元素都是集合B的元素,
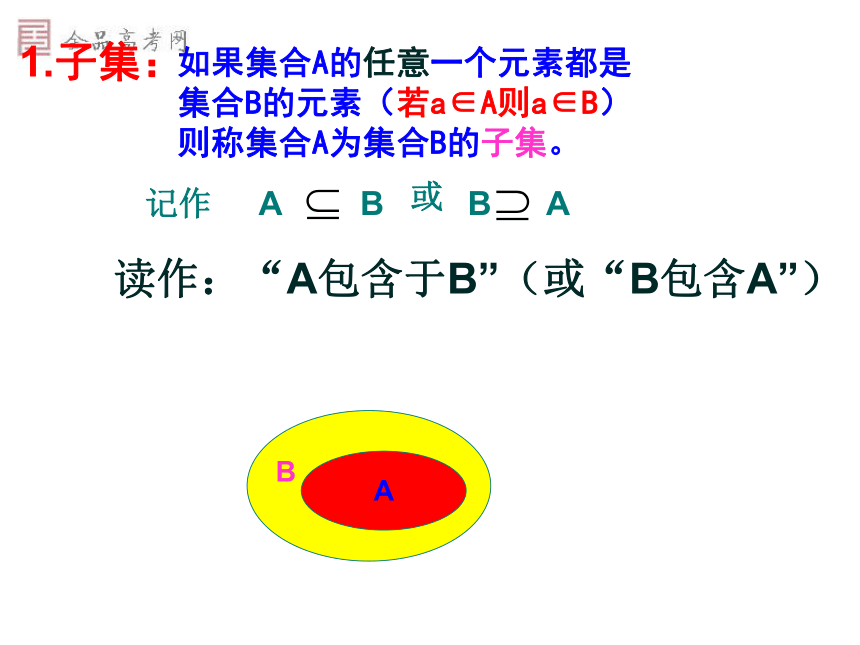
(4)小题中,集合C中的元素和集合D中的元素相同,这两个集合应该相等.1.子集:如果集合A的任意一个元素都是
集合B的元素(若a∈A则a∈B)
则称集合A为集合B的子集。或BAA读作:“A包含于B”(或“B包含A”)练习:
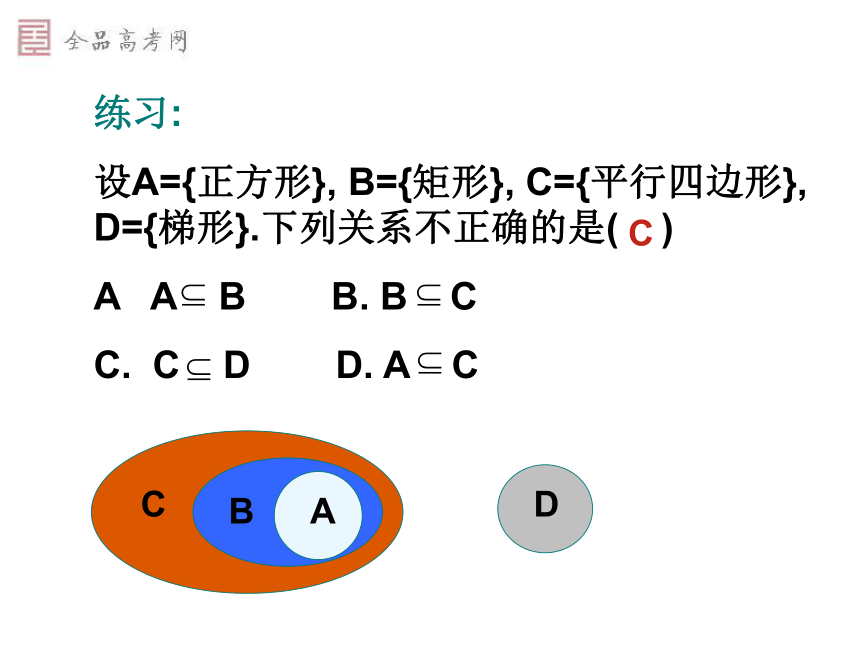
设A={正方形}, B={矩形}, C={平行四边形}, D={梯形}.下列关系不正确的是( )
A A B B. B C
C. C D D. A CCBADC子集的特点:
如果 ,则A必须符合以下条件:① A中的元素都是B中的元素 ② card(A) ≤ card(B)判别A是B的子集的条件真子集:如果集合 ,但存在元素 ,且 ,则称集合A是集合B的真子集,记作A B(或B A)真子集的特点:
如果A B,则A必须符合以下条件① ,即A中的元素必须在B内 ② card(A) < card(B)判别A是B的真子集的条件二、真子集的概念三 集合相等:如果集合A是集合B的子集,且集合B是集A的子集,此时,集合A与集合B中的元素是一样的,因此,集合A与集合B相等,记作A=B练习:判别下列两个集合之间的关系
① A={ 1, 2, 4 } , B={ x | x是8的约数}
②
③A={ x| x是4与10的公倍数, }A BB AA=BABC空集的定义不含任何元素的集合叫做空集
记为:
空集是任何非空集合的真子集.空集是任意集合的子集.1.用适当的符号填空:
(1) 0_____φ
(2) N_____Q
(3) {0}____φ
(4) {0} {{0},{0,1},{1}} 练习: 2.以下六个关系式:① { }
∈{ } ③ {0} φ ④0 φ⑤ φ≠{0} ⑥φ={φ},其中正确的序号是:①②③④⑤要记住的五个结论:(1)对于集合A,B,C,如果A B、B C,那么A C
(2)任何一个集合都是它本身的子集.
(3)空集是任何集合的子集.
(4)空集是任何非空集合的真子集.
(5)空集没有真子集.集合与元素的关系集合与集合的关系属于
不属于包含真包含相等实数< > ≤ ≥=四、区别练习:用恰当的符号填空
①
②
③
④
⑤
⑥
⑦
⑧例1 写出集合{a,b}的所有子集,并指出哪些是它的真子集.
解:集合{a,b}的
所有子集为?,{a},{b},{a,b}.
真子集为 ? ,{a},{b}.
写集合子集的一般方法:先写空集,然后按照集合元素从少到多的顺序写出来,一直到集合本身.写集合真子集时除去集合本身外其余子集都是它的真子集.真子集:写出集合{1,2,3}的所有子集。练习:Φ,{1},{2},{3},{1,2},{1,3},{2,3}思考:集合{a1,a2,…,an}有多少个子集?多少个真子集?多少个非空真子集?2n2n-1{a,b,c,d}2005年天津高考题:集合A={x︱0≤x<3,x∈N}的真子集个数是 ( )
A 16 B 8 C 7 D 4C2n-2Φ,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}课堂练习 练习1 设A={x,x2,xy}, B={1,x,y},且A=B,求实数x,y的值. 练习2 若A={x -3≤x≤4}, B={x 2m-1≤x≤m+1},当B A时,求实数m的取值范围.1、已知集合P={x︱x2+x-6=0},
S ={x︱ax+1=0},若S P,
求实数a的取值集合。2、已知集合A={x︱ax2+2x+1=0,a、x∈R},
至多只有一个真子集,求实数a的取值
集合。能力提高已知集合M满足{1,2} M {1,2,3,4,5},
则这样的集合M共有_______个?82n-m3.五、小结1、子集与真子集的概念2、空集的概念与性质3、对比集合与元素的关系注意符号的使用对象集合之间的基本性质:(1)任何一个集合是它本身的子集,即:
A A;(2)对于集合、A、B、C,如果A B,且B C,那么 A C。作业题:必做:课本习题3
选做:若a、x R,A={2,4,x2-5x+9},
B={3,x2+ax+a},C={x2+(a+1)x-3,1},求:
(1)使A={2,3,4}的X的值;
(2)使2 B,B A的a、x的值;
(3)使B=C的a、x的值。
(1)0 N;(2) Q;(3)-1.5 R
(2)类比实数的大小关系,如5<7,2≤2,试想集合间是否有类似的“大小”关系呢?(4)C={x|x是三条边相等的三角形}
D={x|X是三个内角相等的三角形}他们的关系是:
(1),(2),(3)中集合A中的每一个元素都是集合B的元素,
(4)小题中,集合C中的元素和集合D中的元素相同,这两个集合应该相等.1.子集:如果集合A的任意一个元素都是
集合B的元素(若a∈A则a∈B)
则称集合A为集合B的子集。或BAA读作:“A包含于B”(或“B包含A”)练习:
设A={正方形}, B={矩形}, C={平行四边形}, D={梯形}.下列关系不正确的是( )
A A B B. B C
C. C D D. A CCBADC子集的特点:
如果 ,则A必须符合以下条件:① A中的元素都是B中的元素 ② card(A) ≤ card(B)判别A是B的子集的条件真子集:如果集合 ,但存在元素 ,且 ,则称集合A是集合B的真子集,记作A B(或B A)真子集的特点:
如果A B,则A必须符合以下条件① ,即A中的元素必须在B内 ② card(A) < card(B)判别A是B的真子集的条件二、真子集的概念三 集合相等:如果集合A是集合B的子集,且集合B是集A的子集,此时,集合A与集合B中的元素是一样的,因此,集合A与集合B相等,记作A=B练习:判别下列两个集合之间的关系
① A={ 1, 2, 4 } , B={ x | x是8的约数}
②
③A={ x| x是4与10的公倍数, }A BB AA=BABC空集的定义不含任何元素的集合叫做空集
记为:
空集是任何非空集合的真子集.空集是任意集合的子集.1.用适当的符号填空:
(1) 0_____φ
(2) N_____Q
(3) {0}____φ
(4) {0} {{0},{0,1},{1}} 练习: 2.以下六个关系式:① { }
∈{ } ③ {0} φ ④0 φ⑤ φ≠{0} ⑥φ={φ},其中正确的序号是:①②③④⑤要记住的五个结论:(1)对于集合A,B,C,如果A B、B C,那么A C
(2)任何一个集合都是它本身的子集.
(3)空集是任何集合的子集.
(4)空集是任何非空集合的真子集.
(5)空集没有真子集.集合与元素的关系集合与集合的关系属于
不属于包含真包含相等实数< > ≤ ≥=四、区别练习:用恰当的符号填空
①
②
③
④
⑤
⑥
⑦
⑧例1 写出集合{a,b}的所有子集,并指出哪些是它的真子集.
解:集合{a,b}的
所有子集为?,{a},{b},{a,b}.
真子集为 ? ,{a},{b}.
写集合子集的一般方法:先写空集,然后按照集合元素从少到多的顺序写出来,一直到集合本身.写集合真子集时除去集合本身外其余子集都是它的真子集.真子集:写出集合{1,2,3}的所有子集。练习:Φ,{1},{2},{3},{1,2},{1,3},{2,3}思考:集合{a1,a2,…,an}有多少个子集?多少个真子集?多少个非空真子集?2n2n-1{a,b,c,d}2005年天津高考题:集合A={x︱0≤x<3,x∈N}的真子集个数是 ( )
A 16 B 8 C 7 D 4C2n-2Φ,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}课堂练习 练习1 设A={x,x2,xy}, B={1,x,y},且A=B,求实数x,y的值. 练习2 若A={x -3≤x≤4}, B={x 2m-1≤x≤m+1},当B A时,求实数m的取值范围.1、已知集合P={x︱x2+x-6=0},
S ={x︱ax+1=0},若S P,
求实数a的取值集合。2、已知集合A={x︱ax2+2x+1=0,a、x∈R},
至多只有一个真子集,求实数a的取值
集合。能力提高已知集合M满足{1,2} M {1,2,3,4,5},
则这样的集合M共有_______个?82n-m3.五、小结1、子集与真子集的概念2、空集的概念与性质3、对比集合与元素的关系注意符号的使用对象集合之间的基本性质:(1)任何一个集合是它本身的子集,即:
A A;(2)对于集合、A、B、C,如果A B,且B C,那么 A C。作业题:必做:课本习题3
选做:若a、x R,A={2,4,x2-5x+9},
B={3,x2+ax+a},C={x2+(a+1)x-3,1},求:
(1)使A={2,3,4}的X的值;
(2)使2 B,B A的a、x的值;
(3)使B=C的a、x的值。
