第三章4.2换底公式
图片预览






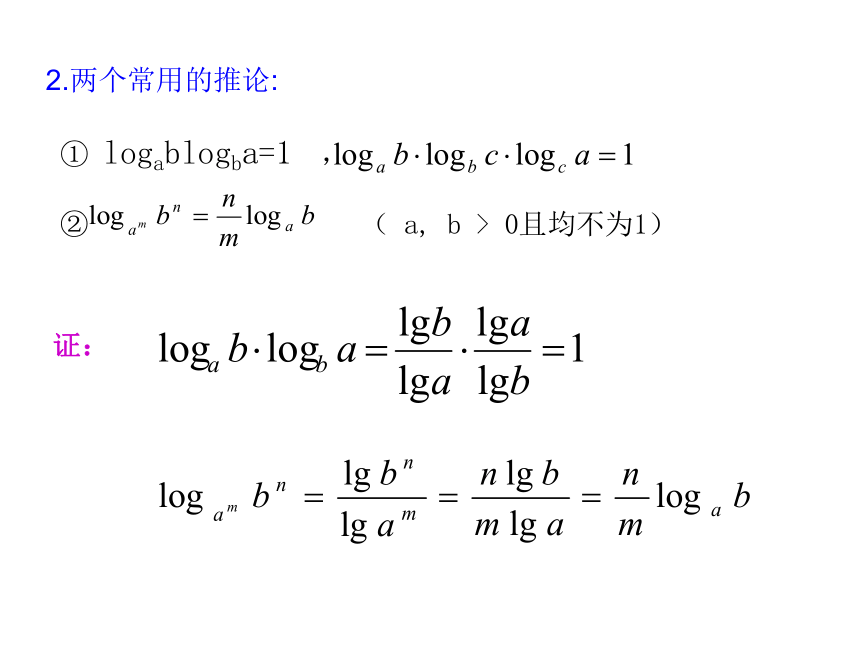
文档简介
课件15张PPT。(一)复习
积、商、幂的对数运算法则:
如果 a > 0,a ? 1,M > 0, N > 0 有:练习:
1.已知lg2=a , lg3=b , 请用a ,b 表示 lg12 .
2.计算lg ( 103-102)的结果( )。
A. 1 B. C. 90 D.2+lg9
解: 1. lg12 =lg(4×3) 2. lg ( 103-102)
=lg4+lg3 = lg [102( 10-1)]
=2lg2+lg3 = lg(102× 9)
=2a +b =lg102+lg9
=2+lg9
解法一: 解法二: ⑴ 若⑵ 的值为______⑶提高练习:2
证明: 设 logaN=x ,则 ax= N,两边取以m为底的对数:
从而得:
∴ (二)、新课:
① logablogba=1 ,
② ( a, b > 0且均不为1)
2.两个常用的推论:证:(三)、讲解范例:
例1 求log89.log2732的值.
一般情况下,可换成常用对数,也可根据真、底数的特征,换成其它合适的底数.
分析:利用换底公式统一底数:
解:因为log23 = a,则 , 又∵ log3 7 = b,
∴
例3 计算:① ②
例2 已知 log2 3 = a, log3 7 = b,用 a, b 表示 log42 56
解:①原式 =
②原式 = 例4
1. 证明:解: 分析:由于x作为真数,故可直接利用对数定义求解;另外,由于等式右端为两实数和的形式,b的存在使变形产生困难,故可考虑将 logac移到等式左端,或者将b变为对数形式
例5 已知 logax= logac+b,求x请大家解决。(四)课堂练习:P86练习:T2,3,4(五)、小结
利用换底公式“化异为同”是解决有关对数问题的基本思想方法,它在求值或恒等变形中作了重要作用,在解题过程中应注意:
1.针对具体问题,选择好底数.
2.注意换底公式与对数运算法则结合使用.
3.换底公式的正用与反用.
1.已知 log18 9 = a , 18b = 5 , 用 a, b 表示 log36 45
2.若 log8 3 = p , log3 5 = q , 求 lg 5
3.已知a = (a﹥0),求log a
4.计算:
(1)log 9+log927+( )log4
(2)7lg20﹒( )lg0.7
作 业
积、商、幂的对数运算法则:
如果 a > 0,a ? 1,M > 0, N > 0 有:练习:
1.已知lg2=a , lg3=b , 请用a ,b 表示 lg12 .
2.计算lg ( 103-102)的结果( )。
A. 1 B. C. 90 D.2+lg9
解: 1. lg12 =lg(4×3) 2. lg ( 103-102)
=lg4+lg3 = lg [102( 10-1)]
=2lg2+lg3 = lg(102× 9)
=2a +b =lg102+lg9
=2+lg9
解法一: 解法二: ⑴ 若⑵ 的值为______⑶提高练习:2
证明: 设 logaN=x ,则 ax= N,两边取以m为底的对数:
从而得:
∴ (二)、新课:
① logablogba=1 ,
② ( a, b > 0且均不为1)
2.两个常用的推论:证:(三)、讲解范例:
例1 求log89.log2732的值.
一般情况下,可换成常用对数,也可根据真、底数的特征,换成其它合适的底数.
分析:利用换底公式统一底数:
解:因为log23 = a,则 , 又∵ log3 7 = b,
∴
例3 计算:① ②
例2 已知 log2 3 = a, log3 7 = b,用 a, b 表示 log42 56
解:①原式 =
②原式 = 例4
1. 证明:解: 分析:由于x作为真数,故可直接利用对数定义求解;另外,由于等式右端为两实数和的形式,b的存在使变形产生困难,故可考虑将 logac移到等式左端,或者将b变为对数形式
例5 已知 logax= logac+b,求x请大家解决。(四)课堂练习:P86练习:T2,3,4(五)、小结
利用换底公式“化异为同”是解决有关对数问题的基本思想方法,它在求值或恒等变形中作了重要作用,在解题过程中应注意:
1.针对具体问题,选择好底数.
2.注意换底公式与对数运算法则结合使用.
3.换底公式的正用与反用.
1.已知 log18 9 = a , 18b = 5 , 用 a, b 表示 log36 45
2.若 log8 3 = p , log3 5 = q , 求 lg 5
3.已知a = (a﹥0),求log a
4.计算:
(1)log 9+log927+( )log4
(2)7lg20﹒( )lg0.7
作 业
