对数函数的图像和性质第2课时(性质的应用)
文档属性
| 名称 | 对数函数的图像和性质第2课时(性质的应用) |  | |
| 格式 | rar | ||
| 文件大小 | 178.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-02-15 15:51:00 | ||
图片预览




文档简介
课件18张PPT。复习上节内容 1、对数函数 y = log a x ( a>0 且 a ≠1 ) 是
指数函数 y = a x ( a>0 且 a ≠1 ) 的反函数。2、对数函数的图象与性质:例1、比较下列各组数中两个数的大小:
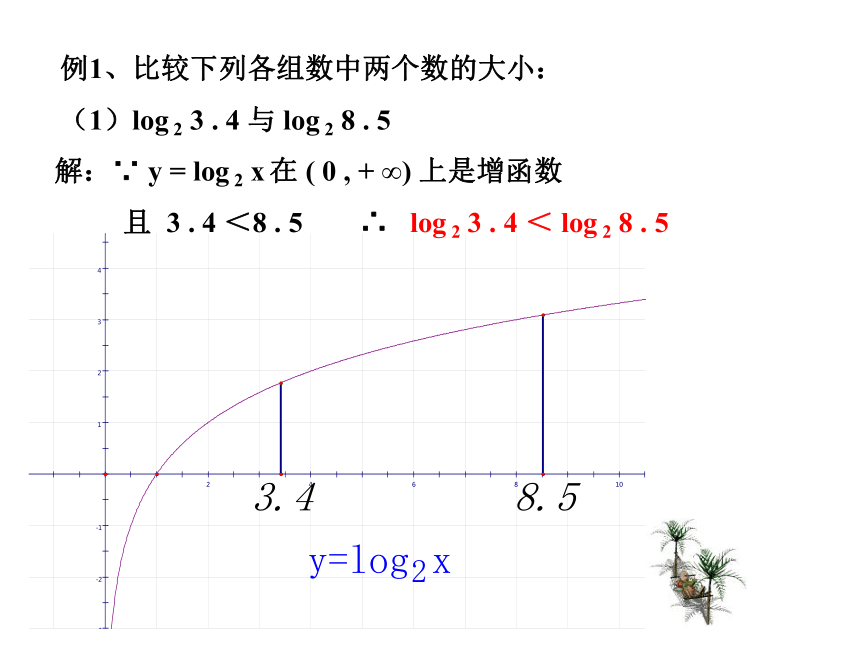
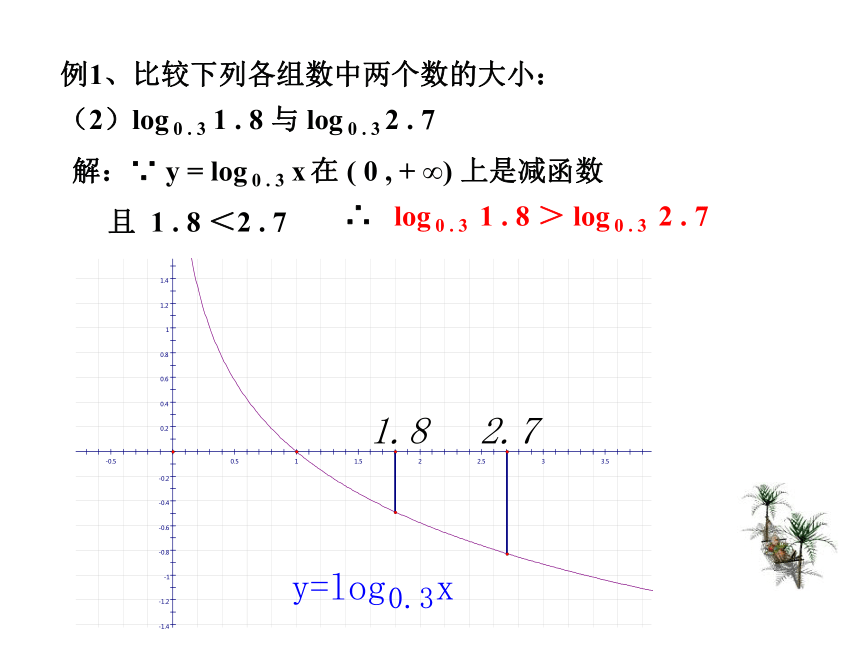
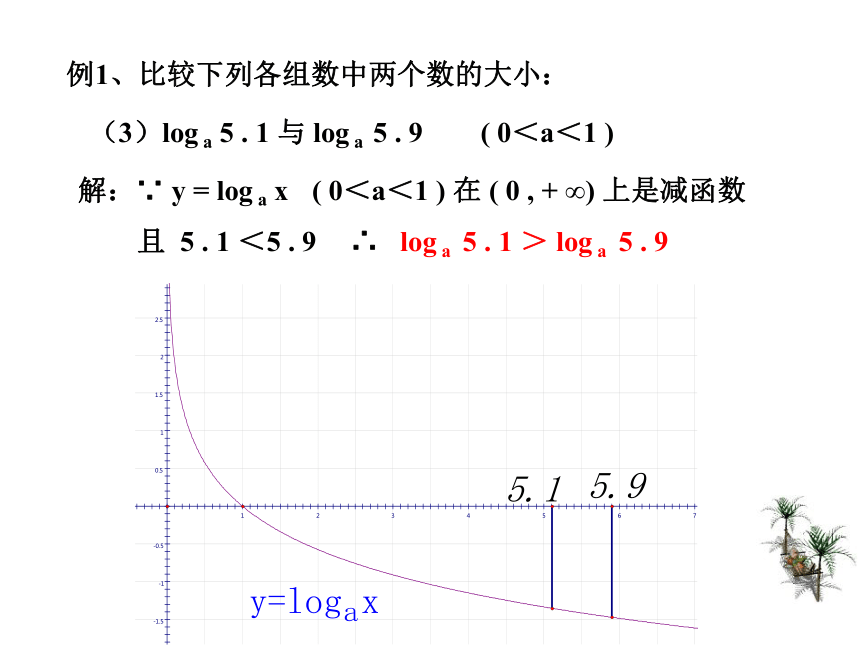
(1)log 2 3 . 4 与 log 2 8 . 5 解:∵ y = log 2 x 在 ( 0 , + ∞) 上是增函数且 3 . 4 <8 . 5∴ log 2 3 . 4 < log 2 8 . 5 例1、比较下列各组数中两个数的大小:(2)log 0 . 3 1 . 8 与 log 0 . 3 2 . 7解:∵ y = log 0 . 3 x 在 ( 0 , + ∞) 上是减函数且 1 . 8 <2 . 7∴ log 0 . 3 1 . 8 > log 0 . 3 2 . 7 例1、比较下列各组数中两个数的大小:(3)log a 5 . 1 与 log a 5 . 9 ( 0<a<1 )解:∵ y = log a x ( 0<a<1 ) 在 ( 0 , + ∞) 上是减函数且 5 . 1 <5 . 9∴ log a 5 . 1 > log a 5 . 9 例2:比较下列各组数中两个值的大小:
(1)log 6 7 与 log 7 6解:∵ log 6 7 > log 6 6 = 1 且 log 7 6 < log 7 7 = 1 ∴ log 6 7 > log 7 6(2) log 3 π 与 log 2 0 . 8解:∵ log 3 π > log 3 1 = 0 且 log 2 0 . 8 < log 2 1 = 0 ∴ log 3 π > log 2 0 . 8例2:比较下列各组数中两个值的大小:(3) log 2 7 与 log 3 7解:∵ log 7 3 > log 7 2 >0∴ log 2 7 > log 3 7(4) log 0 . 2 0 . 8 与 log 0 . 3 0 . 8解:∵ log 0 . 8 0 . 2 > log 0 . 8 0 . 3且 log 0 . 8 0 . 2 、 log 0 . 8 0 . 3 >0∴ log 0 . 2 0 . 8 < log 0 . 3 0 . 8例3、设 0<x<1,a>0 且 a≠1,试比较
| log a ( 1-x ) | 与 | log a ( 1 + x ) | 的大小。| log a ( 1-x ) | - | log a ( 1 + x ) | ∵ 0<x<1∴ 0<1-x<1<1 + x <2即 | log a ( 1-x ) | - | log a ( 1 + x ) | >0∴ | log a ( 1-x ) | > | log a ( 1 + x ) |解:当01时,则有=-log a ( 1-x ) -log a ( 1 + x ) =-log a ( 1-x ) ( 1 + x ) | log a ( 1-x ) | > | log a ( 1 + x ) |当a>1时,有当0(1)求 f ( x ) 的定义域;解:由题 a x -b x >0 得 a x > b x∵ a>1>b>0∴ x >0故 f ( x ) 的定义域为 ( 0 , + ∞ )∴ 例5、已知 f ( x ) = lg ( a x -b x ) ( a>1>b>0 )(2)判断 f ( x ) 的单调性。解:设 0<x 1<x 2 < + ∞,则 f ( x 1 ) -f ( x 2 ) =∵ a>1>b>0即 f ( x 1 ) -f ( x 2 ) <0∴ f ( x 1 ) < f ( x 2 ) 故 f ( x ) 在( 0 , + ∞ ) 上是增函数(3)此函数的图象上不存在不同两点,使过两点直线平行
于 x 轴。证:设 A ( x 1 , y 1 )、B ( x 2 , y 2 ) 且 x 1 ≠ x 2∵ f ( x ) 在( 0 , + ∞ ) 上是增函数∴ y 1 ≠ y 2故 过这两点的直线不平行于 x 轴。例5、已知 f ( x ) = lg ( a x -b x ) ( a>1>b>0 )∴ 当x 1 y 2 当x 1 >x 2时,例5、已知 f ( x ) = lg ( a x -b x ) ( a>1>b>0 )(4)当 a、b 满足什么条件时,f ( x ) 在区间 [ 1 , + ∞) 上恒
为正。解:∵ f ( x ) 在( 0 , + ∞ ) 上是增函数∴ f ( x ) min = f ( 1 ) = lg ( a -b )只要使 lg ( a -b ) > 0就可以了,故满足 a -b >1 要使f ( x ) 在区间 [ 1 , + ∞) 上恒为正。(一)同底数比较大小时
1、当底数确定时,则可由函数的单调
性直接进行判断。
2、当底数不确定时,应对底数进
行分类讨论(三)若底数、真数都不相同, 则常借
助1、0等中间量进行比较 (二)同真数的比较大小, 常借助函数图象 进行比较 小结:两个对数比较大小同学们 再见!
指数函数 y = a x ( a>0 且 a ≠1 ) 的反函数。2、对数函数的图象与性质:例1、比较下列各组数中两个数的大小:
(1)log 2 3 . 4 与 log 2 8 . 5 解:∵ y = log 2 x 在 ( 0 , + ∞) 上是增函数且 3 . 4 <8 . 5∴ log 2 3 . 4 < log 2 8 . 5 例1、比较下列各组数中两个数的大小:(2)log 0 . 3 1 . 8 与 log 0 . 3 2 . 7解:∵ y = log 0 . 3 x 在 ( 0 , + ∞) 上是减函数且 1 . 8 <2 . 7∴ log 0 . 3 1 . 8 > log 0 . 3 2 . 7 例1、比较下列各组数中两个数的大小:(3)log a 5 . 1 与 log a 5 . 9 ( 0<a<1 )解:∵ y = log a x ( 0<a<1 ) 在 ( 0 , + ∞) 上是减函数且 5 . 1 <5 . 9∴ log a 5 . 1 > log a 5 . 9 例2:比较下列各组数中两个值的大小:
(1)log 6 7 与 log 7 6解:∵ log 6 7 > log 6 6 = 1 且 log 7 6 < log 7 7 = 1 ∴ log 6 7 > log 7 6(2) log 3 π 与 log 2 0 . 8解:∵ log 3 π > log 3 1 = 0 且 log 2 0 . 8 < log 2 1 = 0 ∴ log 3 π > log 2 0 . 8例2:比较下列各组数中两个值的大小:(3) log 2 7 与 log 3 7解:∵ log 7 3 > log 7 2 >0∴ log 2 7 > log 3 7(4) log 0 . 2 0 . 8 与 log 0 . 3 0 . 8解:∵ log 0 . 8 0 . 2 > log 0 . 8 0 . 3且 log 0 . 8 0 . 2 、 log 0 . 8 0 . 3 >0∴ log 0 . 2 0 . 8 < log 0 . 3 0 . 8例3、设 0<x<1,a>0 且 a≠1,试比较
| log a ( 1-x ) | 与 | log a ( 1 + x ) | 的大小。| log a ( 1-x ) | - | log a ( 1 + x ) | ∵ 0<x<1∴ 0<1-x<1<1 + x <2即 | log a ( 1-x ) | - | log a ( 1 + x ) | >0∴ | log a ( 1-x ) | > | log a ( 1 + x ) |解:当0
于 x 轴。证:设 A ( x 1 , y 1 )、B ( x 2 , y 2 ) 且 x 1 ≠ x 2∵ f ( x ) 在( 0 , + ∞ ) 上是增函数∴ y 1 ≠ y 2故 过这两点的直线不平行于 x 轴。例5、已知 f ( x ) = lg ( a x -b x ) ( a>1>b>0 )∴ 当x 1
为正。解:∵ f ( x ) 在( 0 , + ∞ ) 上是增函数∴ f ( x ) min = f ( 1 ) = lg ( a -b )只要使 lg ( a -b ) > 0就可以了,故满足 a -b >1 要使f ( x ) 在区间 [ 1 , + ∞) 上恒为正。(一)同底数比较大小时
1、当底数确定时,则可由函数的单调
性直接进行判断。
2、当底数不确定时,应对底数进
行分类讨论(三)若底数、真数都不相同, 则常借
助1、0等中间量进行比较 (二)同真数的比较大小, 常借助函数图象 进行比较 小结:两个对数比较大小同学们 再见!
