勾股定理同步练习
图片预览



文档简介
第十八章 勾股定理
18.1勾股定理(1)
预习练习:
1. 在直角三角形ABC中,斜边AB=1,则AB的值是( )
A.2 B.4 C.6 D.8
2. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,
在花铺内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),
却踩伤了花草.
3. 直角三角形两直角边长分别为5和12,则它斜边上的高为_______.
4. 如图所示,一根旗杆于离地面12处断裂,犹如装有铰链那样倒向地面,旗杆顶落于离旗杆地步16,旗杆在断裂之前高多少?
5.如图,如下图,今年的冰雪灾害中,一棵大树在离地面3米处折断,树的顶端落在离树杆底部4米处,那么这棵树折断之前的高度是 米.
课堂练习:
1.在直角三角形中,若两直角边的长分别为1cm,2cm ,则斜边长为_____________.
2.已知直角三角形的两边长为3、2,则另一条边长是________________.
3.在一个直角三角形中,若斜边长为5cm,直角边的长为3cm,则另一条直角边的长为( ).
A.4cm B.4cm或 C. D.不存在
4.在数轴上作出表示的点.
5.一种盛饮料的圆柱形杯,测得内部底面半径为2.5㎝,
高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?
6. 飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米,求飞机每小时飞行多少千米
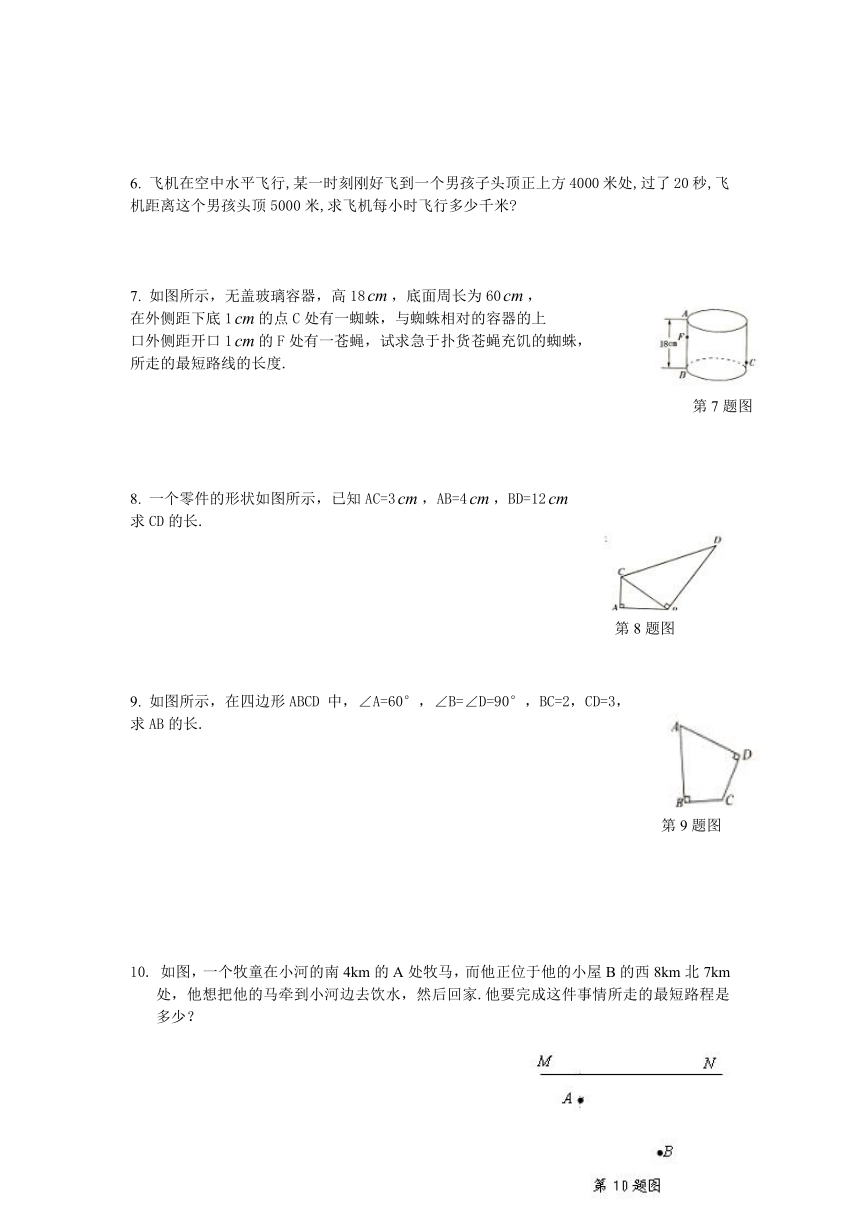
7. 如图所示,无盖玻璃容器,高18,底面周长为60,
在外侧距下底1的点C处有一蜘蛛,与蜘蛛相对的容器的上
口外侧距开口1的F处有一苍蝇,试求急于扑货苍蝇充饥的蜘蛛,
所走的最短路线的长度.
8. 一个零件的形状如图所示,已知AC=3,AB=4,BD=12
求CD的长.
9. 如图所示,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,
求AB的长.
10. 如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
课后练习:
1.把一根长为10㎝的铁丝弯成一个直角三角形的两条直角边,如果要使三角形的面积是9㎝2,那么还要准备一根长为____的铁丝才能把三角形做好.
2.如图,将一个边长分别为4、8的长方形纸片ABCD折叠,使C点与A点重合,则EB的长是( ).
A.3 B.4
C. D.5
3.如图:带阴影部分的半圆的面积是多少?(取3)
4.已知,如图在ΔABC中,AB=BC=CA=2cm,AD是边BC上的高.
求 ①AD的长; ②ΔABC的面积.
5.在直角ΔABC中,斜边长为2,周长为2+,求ΔABC的面积.
6.已知:如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线交BC于D,垂足为E,BD=4cm.求AC的长.
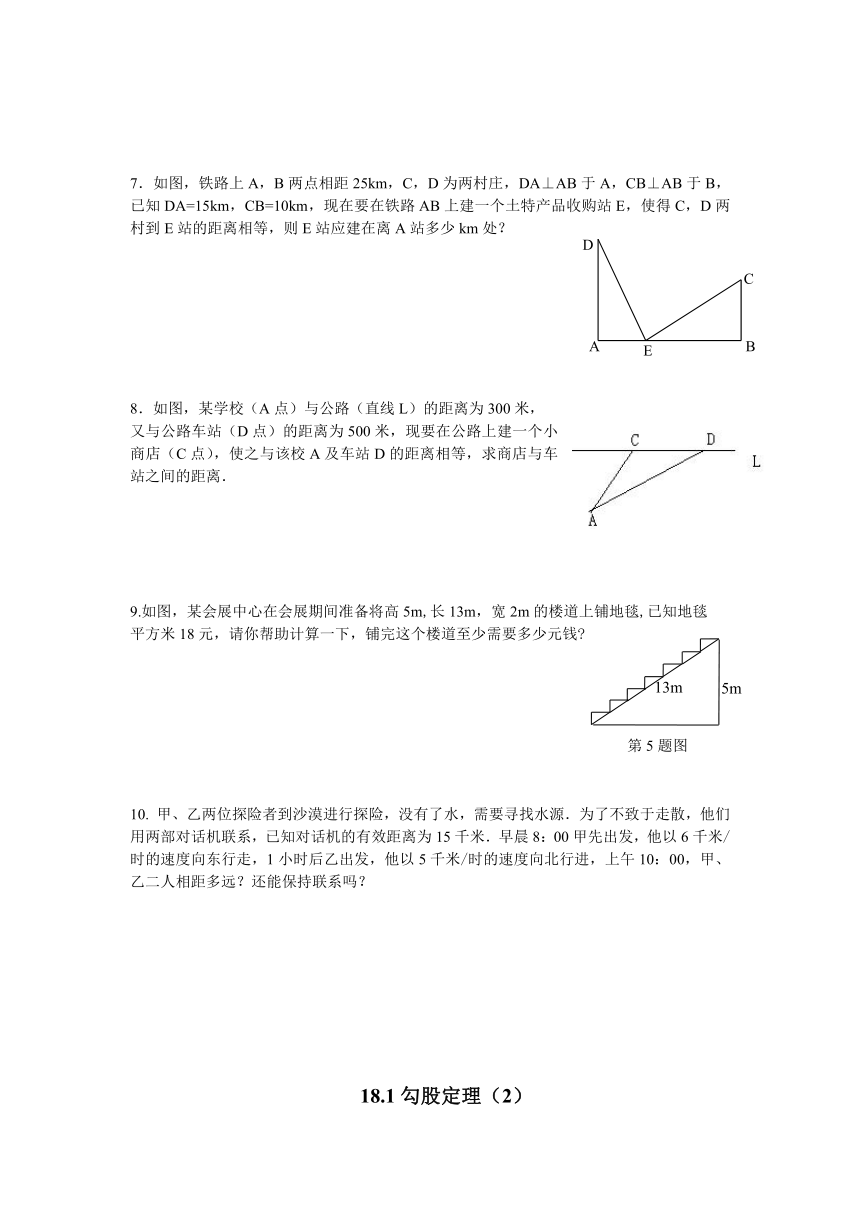
7.如图,铁路上A,B两点相距25km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
8.如图,某学校(A点)与公路(直线L)的距离为300米,
又与公路车站(D点)的距离为500米,现要在公路上建一个小商店(C点),使之与该校A及车站D的距离相等,求商店与车站之间的距离.
9.如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯
平方米18元,请你帮助计算一下,铺完这个楼道至少需要多少元钱
10. 甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为15千米.早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?
18.1勾股定理(2)
预习练习:
1. 下列说法正确的是( )
A.若 a、b、c是△ABC的三边,则a2+b2=c2
B.若 a、b、c是Rt△ABC的三边,则a2+b2=c2
C.若 a、b、c是Rt△ABC的三边,,则a2+b2=c2
D.若 a、b、c是Rt△ABC的三边,,则a2+b2=c2
2. △ABC的三条边长分别是、、,则下列各式成立的是( )
A. B. C. D.
3.一个直角三角形中,两直角边长分别为3和4,下列说法正确的是( )
A.斜边长为25 B.三角形周长为25
C.斜边长为5 D.三角形面积为20
4.在中, ,
(1)如果a=3,b=4,则c= ;
(2)如果a=6,b=8,则c= ;
(3)如果a=5,b=12,则c= ;
(4) 如果a=15,b=20,则c= .
5.如图,三个正方形中的两个的面积S1=25,S2=144,则另一个的面积S3为_______
课堂练习:
1.直角三角形中,以直角边为边长的两个正方形的面积为7,8,则以斜边为边长的正方形的面积为_________.
2.如图一个圆柱,底圆周长6cm,高4cm,一只蚂蚁沿外
壁爬行,要从A点爬到B点,则最少要爬行 cm
3.小雨用竹杆扎了一个长80cm、宽60cm的长方形框架,由于四边形容易变形,需要用一根竹杆作斜拉杆将四边形定形,则斜拉杆最长需________cm .
4.小杨从学校出发向南走150米,接着向东走了360米到九龙山商场,学校与九龙山商场的距离是 米.
5.已知直角三角形两直角边长分别为5和12, 求斜边上的高.
6.利用四个全等的直角三角形可以拼成如图所示的图形,这个图形被称为弦图.观察图形,验证:c2=a2+b2.
7.如图,小李准备建一个蔬菜大棚,棚宽4m,高3m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请计算阳光透过的最大面积.
8.下面是数学课堂的一个学习片段, 阅读后, 请回答下面的问题:
学习勾股定理有关内容后, 张老师请同学们交流讨论这样一个问题: “已知直角三角形ABC的两边长分别为3和4, 请你求出第三边.”
同学们经片刻的思考与交流后, 李明同学举手说: “第三边长是5”; 王华同学说: “第三边长是.” 还有一些同学也提出了不同的看法……
(1)假如你也在课堂上, 你的意见如何 为什么
(2)通过上面数学问题的讨论, 你有什么感受 (用一句话表示)
9.蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)
10.已知:如图,△ABC中,AB>AC,AD是BC边上的高.
求证:AB2-AC2=BC(BD-DC).
课后练习:
1.已知直角三角形中30°角所对的直角边长是cm,则另一条直角边的长是( )
A. 4cm B. cm C. 6cm D. cm
2.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42 B.32 C.42 或 32 D.37 或 33
3.一架25分米长的梯子,斜立在一竖直的墙上,这时梯足距离墙底端7分米.如果梯子的顶端沿墙下滑4分米,那么梯足将滑动( )
A. 9分米 B. 15分米 C. 5分米 D. 8分米
4. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草.
5. 在△ABC中,∠C=90°,(1)已知 a=2.4,b=3.2,则c= ;(2)已知c=17,b=15,则△ABC面积等于 ;(3)已知∠A=45°,c=18,则a= .
6. 一个矩形的抽斗长为24cm,宽为7cm,在里面放一根铁条,那么铁条最长可以是 .
7.小明想测量学校旗杆的高度,他采用如下的方法:先降旗
杆上的绳子接长一些,让它垂到地面还多1米,然后将绳子
下端拉直,使它刚好接触地面,测得绳下端离旗杆底部5米,
你能帮它计算一下旗杆的高度.
8.有一只鸟在一棵高4米的小树梢上捉虫子,它的伙伴在离该树12米,高20米的一棵大树的树梢上发出友好的叫声,它立刻以4米/秒的速度飞向大树树梢.那么这只鸟至少几秒才能到达大树和伙伴在一起.
9. 如图∠B=90 ,AB=16cm,BC=12cm,AD=21cm,CD=29cm
求四边形ABCD的面积.
10.如图,一个梯子AB长2.5 米,顶端A靠在墙AC上,这时
梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置
上,测得BD长为0.5米,求梯子顶端A下落了多少米?
18.2 勾股定理的逆定理(1)
预习练习:
1. 分别以下列四组数为一个三角形的边长:(1)3,4,5;(2)5,12,13;(3)8,15,17;(4)4,5,6.其中能构成直角三角形的有( )
A.4组 B.3组 C.2组 D.1组
2. 三角形的三边长分别为 a2+b2、2ab、a2-b2(a、b都是正整数),则这个三角形是()
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
3.如果把直角三角形的两条直角边同时扩大到原来的2倍,那么斜边扩大到原来的( )
A.1倍 B. 2倍 C. 3倍 D. 4倍
4. 下列各命题的逆命题不成立的是( )
A.两直线平行,同旁内角互补 B.若两个数的绝对值相等,则这两个数也相等
C.对顶角相等 D.如果a=b,那么a2=b2
5.五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是( )
A B C D
课堂练习:
1.若△ABC的三个外角的度数之比为3:4:5,最大边AB与最小边BC的关系是_________.
2.若一个三角形的周长12cm,一边长为3cm,其他两边之差为cm,则这个三角形
是______________________.
3.将直角三角形的三边扩大相同的倍数后,得到的三角形是 ( ).
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不是直角三角形
4满足下列条件的三角形中,不是直角三角形的是( )
A.三个内角比为1∶2∶1 B.三边之比为1∶2∶
C.三边之比为∶2∶ D. 三个内角比为1∶2∶3
5.下列命题中是假命题的是( ).
A.△ABC中,若∠B=∠C-∠A,则△ABC是直角三角形.
B.△ABC中,若a2=(b+c)(b-c),则△ABC是直角三角形.
C.△ABC中,若∠A∶∠B∶∠C=3∶4∶5则△ABC是直角三角形.
D.△ABC中,若a∶b∶c=5∶4∶3则△ABC是直角三角形.
6.在△ABC中,,那么△ABC是( ).
A.等腰三角形 B.钝角三角形 C.直角三角形 D.等腰直角三角形
7.如图,四边形ABCD中,F为DC的中点,E为BC上一点,
且.你能说明∠AFE是直角吗?
8. 如图所示的一块地,已知AD=4m,CD=3m, AD⊥DC,AB=13m,BC=12m,求这块地的面积.
9. 一个零件的形状如左图所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如右图所示,这个零件符合要求吗?
10. 如图,E、F分别是正方形ABCD中BC和CD边上的点,且AB=4,CE=BC,F为CD的中点,连接AF、AE,问△AEF是什么三角形?请说明理由.
课后练习:
1.下列各组数据中,不能作为直角三角形三边长的是( )
A.9,12,15 B. C.0.2,0.3,0.4 D.40,41,9
2.已知三角形两边长为2和6,要使这个三角形为直角三角形,则第三边的长为( )
A. B. C. D.以上都不对
3. △ABC的三边分别是7、24、25,则三角形的最大内角的度数是 .
4.三边为9、12、15的三角形,其面积为 .
5.已知三角形ABC的三边长为满足,,则此三角形为
三角形.
6.在三角形ABC中,AB=12,AC=5,BC=13,则BC边上的高为AD= .
7. 如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,
求四边形ABCD的面积.
8. 如图,E、F分别是正方形ABCD中BC和CD边上的点,且AB=4,CE=BC,F为CD的中点,连接AF、AE,问△AEF是什么三角形?请说明理由.
9. 如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的
C处有一筐水果,一只猴子从D处上爬到树顶A处,
利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处
滑到地面B,再由B跑到C,已知两猴子所经路程都是15m,
求树高AB.
10. 观察下列勾股数:
第一组:3=2×1+1, 4=2×1×(1+1), 5=2×1×(1+1)+1;
第二组:5=2×2+1, 12=2×2×(2+1), 13=2×2×(2+1)+1;
第三组:7=2×3+1, 24=2×3×(3+1), 25=2×3×(3+1)+1;
第三组:9=2×4+1, 40=2×4×(4+1), 41=2×4×(4+1)+1;
……
观察以上各组勾股数的组成特点,你能求出第七组的各应是多少吗?第组呢?
18.2 勾股定理的逆定理(2)
预习练习:
1. 如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是( )
A.7,24,25 B.3,4,5 C.3,4,5 D.4,7,8
2.在下列说法中是错误的( )
A.在△ABC中,∠C=∠A一∠B,则△ABC为直角三角形.
B.在△ABC中,若∠A:∠B:∠C=5:2:3,则△ABC为直角三角形.
C.在△ABC中,若a=c,b=c,则△ABC为直角三角形.
D.在△ABC中,若a:b:c=2:2:4,则△ABC为直角三角形.
3. 有六根细木棒,它们的长度分别为2,4,6,8,10,12(单位:cm),从中取出三根首尾顺次连接搭成一个直角三角形,则这根木棒的长度分别为( )
A.2,4,8 B.4,8,10 C.6,8,10 D.8,10,12
4.将勾股数3,4,5扩大2倍,3倍,4倍,…,可以得到勾股数6,8,10;9,12,15;12,16,20;…,则我们把3,4,5这样的勾股数称为基本勾股数,请你也写出三组基本勾股数 , , .
5.若三角形的两边长为4和5,要使其成为直角三角形,则第三边的长为 .
课堂练习:
1.△ABC的三边分别为a=3cm,b=4cm,c=5cm,则△ABC中的最小角为_____。
2. 已知直角三角形的两边长分别为3、4,则第三边的平方为__________。
3.分别以下列四组数为一个三角形的边长:(1)6、8、10;(2)13、12、5;(3)1、2、3;
(4)4、5、6.其中能构成直角三角形的有( )
A.4组 B.3组 C.2组 D.1组
4. 已知△ABC的三边为a、b、c,有下列各组条件,判断△ABC的形状。
a=41,b=40,c=9;
5. 在△ABC中,AB=15,BD=14,AD=13,求BD边上的高AC。
6. 在四边形ABCD中, C是直角,AB=13,BC=4,CD=3,AD=12,求证:AD⊥BD
7.如图,已知等腰△ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,求△ABC的周长.
8.如图,三个村庄A、B、C之间的距离分别为AB=5km,BC=12km,AC=13km.要从B修一条公路BD直达AC.已知公路的造价为26000元/km,求修这条公路的最低造价是多少?
9.如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处上爬到树顶A处,利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处滑到地面B,再由B跑到C,已知两猴子所经路程都是15m,求树高AB.
10.如图,在△ABC中,∠ACB=90 ,AC=BC,P是△ABC内的一点,且PB=1,PC=2,PA=3,求∠BPC的度数.
课后练习:
1.已知在一个三角形ABC中,BC=6,BC边上的高为7,若AC=5,则AC边上的高为 _________.
2.已知一个三角形的三边分别为3k,4k,5k(k为自然数),则这个三角形为______,理由是_______.
3.一个三角形的三边分别为7cm,24 cm,25 cm,则此三角形的面积为_________。
4.若一个三角形的三边之比为5:12:13,且周长为60cm,则它的面积为_________。 .
5.给出下列几组数:① ;②8,15,16;③n2-1,2n,n2+1;④m2-n2,2mn,m2+n2(m>n>0).其中—定能组成直角三角形三边长的是( ).
A.①② B.③④ C.①③④ D.④
6.下列各组数能构成直角三角形三边长的是( ).
A.1,2,3 B.4,5,6 C.12,13,14 D.9,40,41
7.等边三角形的三条高把这个三角形分成直角三角形的个数是( ).
A.8个 B.10个 C.11个 D.12个
8.如果一个三角形一边的平方为2(m2+1),其余两边分别为m-1,m + l,那么这个三角形是( );
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
9. 下列数组中,能组成一个直角三角形的有( )
(1) 15,20,25;(2)10,24,25;(3)9,80,81;(4)8,15,17
A.1组 B.2组 C.3组 D.4组
10.我们知道,以3,4,5为边长的三角形为直角三角形,称3,4,5为勾股数组,记为(3,4,5),类似地,还可得到下列勾股数组:(8,6,10),(15,8,17),(24,10,26)等.
(1)请你根据上述四组勾股数的规律,写出第六组勾股数;
(2)试用数学等式描述上述勾股数组的规律;
(3)请证明你所发现的规律.
第十八章《勾股定理》测试题
(时间:100分钟 总分:100分)
一、相信你一定能选对!(每小题3分,共24分)
1. 三角形的三边长分别为6,8,10,它的最短边上的高为( )
A. 6 B. 4.5 C. 2.4 D. 8
2. 下面几组数:①7,8,9;②12,9,15;③m2 + n2, m2–n2, 2mn(m,n均为正整数,mn);④,,.其中能组成直角三角形的三边长的是( )
A. ①② B. ②③ C. ①③ D. ③④
3. 三角形的三边为a、b、c,由下列条件不能判断它是直角三角形的是( )
A.a:b:c=8∶16∶17 B. a2-b2=c2
C.a2=(b+c)(b-c) D. a:b:c =13∶5∶12
4. 三角形的三边长为,则这个三角形是( )
A. 等边三角形 B. 钝角三角形 C. 直角三角形 D. 锐角三角形.
5.已知一个直角三角形的两边长分别为3和4,则第三边长是( )
A.5 B.25 C. D.5或
6.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是( )
A. 24cm2 B. 36cm2 C. 48cm2 D. 60cm2
7.直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )
A.121 B.120 C.90 D.不能确定
8. 放学以后,小红和小颖从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖20分钟到家,小红和小颖家的直线距离为( )
A.600米 B. 800米 C. 1000米 D. 不能确定
二、你能填得又快又对吗?(每小题3分,共24分)
9. 在△ABC中,∠C=90°, AB=5,则++=_______.
10. 如图,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成.如果图中大、小正方形的面积分别为52和4,那么一个直角三角形的两直角边的和等于 .
11.直角三角形两直角边长分别为5和12,则它斜边上的高为_______.
12.直角三角形的三边长为连续偶数,则这三个数分别为__________.
13. 如图,一根树在离地面9米处断裂,树的顶部落在离底部12米处.树折断之前有 米.
14.如图所示,是一个外轮廓为矩形的机器零件平面示意图,根据图中标出尺寸(单位:mm)计算两圆孔中心A和B的距离为 .
15.如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2米,梯子的顶端B到地面的距离为7米.现将梯子的底端A向外移动到A’,使梯子的底端A’到墙根O的距离等于3米,同时梯子的顶端 B下降至 B’,那么 BB’的值: ①等于1米;②大于1米5;③小于1米.其中正确结论的序号是 .
16.小刚准备测量河水的深度,他把一根竹竿插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,河水的深度为 .
三、认真解答,一定要细心哟!(共52分)
17.(5分)右图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试分别画出一条长度是有理数的线段和一条长度是无理数的线段.
18.(5分)已知a、b、c是三角形的三边长,a=2n2+2n,b=2n+1,c=2n2+2n+1(n为大于1的自然数),试说明△ABC为直角三角形.
19.(5分)小东拿着一根长竹竿进一个宽为3米的城门,他先横着拿不进去,又竖起来拿,结果竿比城门高1米,当他把竿斜着时,两端刚好顶着城门的对角,问竿长多少米?
20.(5分)如图所示,某人到岛上去探宝,从A处登陆后先往东走4km,又往北走1.5km,遇到障碍后又往西走2km,再折回向北走到4.5km处往东一拐,仅走0.5km就找到宝藏。问登陆点A与宝藏埋藏点B之间的距离是多少?
21.(5分)如图,将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和10㎝的长方体无盖盒子中,求细木棒露在盒外面的最短长度是多少?
22.(5分)印度数学家什迦逻(1141年-1225年)曾提出过“荷花问题”:
“平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅?”
请用学过的数学知识回答这个问题.
23.(5分)如图,甲乙两船从港口A同时出发,甲船以16海里/时速度向北偏东40°航行,乙船向南偏东50°航行,3小时后,甲船到达C岛,乙船到达B岛.若C、B两岛相距60海里,问乙船的航速是多少?
24.(5分)如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿
∠CAB的角平分线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
25.(6分)如图,铁路上A、B两点相距25km, C、D为两村庄,若DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.求E应建在距A多远处?
26.(6分)如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
第5题图
第7题图
第8题图
第9题图
5m
13m
第5题图
A
D
E
B
C
8
6
A
E
C
D
B
A
第5题图
S1
S2
S3
3m
4m
20m
D
A
C
C
B
A
D
第4题图
D
C
B
F
E
A
C
B
D
第7题图
F
E
A
C
B
D
第8题图
B
A
C
D
.
第9题图
D
B
C
A
B
12 5
C 路、 D..13 D A
B
A
C
D
.
A
C
P
B
60
1200
140
60
B
A
C
第10题图
第13题图
第14题图
第15题图
A
B
4
1.5
2
4.5
0.5
A
C
B
A
E
C
D
B
C
A
B
D
E
10
15
A
B
小河
东
北
牧童
小屋
18.1勾股定理(1)
预习练习:
1. 在直角三角形ABC中,斜边AB=1,则AB的值是( )
A.2 B.4 C.6 D.8
2. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,
在花铺内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),
却踩伤了花草.
3. 直角三角形两直角边长分别为5和12,则它斜边上的高为_______.
4. 如图所示,一根旗杆于离地面12处断裂,犹如装有铰链那样倒向地面,旗杆顶落于离旗杆地步16,旗杆在断裂之前高多少?
5.如图,如下图,今年的冰雪灾害中,一棵大树在离地面3米处折断,树的顶端落在离树杆底部4米处,那么这棵树折断之前的高度是 米.
课堂练习:
1.在直角三角形中,若两直角边的长分别为1cm,2cm ,则斜边长为_____________.
2.已知直角三角形的两边长为3、2,则另一条边长是________________.
3.在一个直角三角形中,若斜边长为5cm,直角边的长为3cm,则另一条直角边的长为( ).
A.4cm B.4cm或 C. D.不存在
4.在数轴上作出表示的点.
5.一种盛饮料的圆柱形杯,测得内部底面半径为2.5㎝,
高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?
6. 飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米,求飞机每小时飞行多少千米
7. 如图所示,无盖玻璃容器,高18,底面周长为60,
在外侧距下底1的点C处有一蜘蛛,与蜘蛛相对的容器的上
口外侧距开口1的F处有一苍蝇,试求急于扑货苍蝇充饥的蜘蛛,
所走的最短路线的长度.
8. 一个零件的形状如图所示,已知AC=3,AB=4,BD=12
求CD的长.
9. 如图所示,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,
求AB的长.
10. 如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
课后练习:
1.把一根长为10㎝的铁丝弯成一个直角三角形的两条直角边,如果要使三角形的面积是9㎝2,那么还要准备一根长为____的铁丝才能把三角形做好.
2.如图,将一个边长分别为4、8的长方形纸片ABCD折叠,使C点与A点重合,则EB的长是( ).
A.3 B.4
C. D.5
3.如图:带阴影部分的半圆的面积是多少?(取3)
4.已知,如图在ΔABC中,AB=BC=CA=2cm,AD是边BC上的高.
求 ①AD的长; ②ΔABC的面积.
5.在直角ΔABC中,斜边长为2,周长为2+,求ΔABC的面积.
6.已知:如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线交BC于D,垂足为E,BD=4cm.求AC的长.
7.如图,铁路上A,B两点相距25km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
8.如图,某学校(A点)与公路(直线L)的距离为300米,
又与公路车站(D点)的距离为500米,现要在公路上建一个小商店(C点),使之与该校A及车站D的距离相等,求商店与车站之间的距离.
9.如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯
平方米18元,请你帮助计算一下,铺完这个楼道至少需要多少元钱
10. 甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为15千米.早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?
18.1勾股定理(2)
预习练习:
1. 下列说法正确的是( )
A.若 a、b、c是△ABC的三边,则a2+b2=c2
B.若 a、b、c是Rt△ABC的三边,则a2+b2=c2
C.若 a、b、c是Rt△ABC的三边,,则a2+b2=c2
D.若 a、b、c是Rt△ABC的三边,,则a2+b2=c2
2. △ABC的三条边长分别是、、,则下列各式成立的是( )
A. B. C. D.
3.一个直角三角形中,两直角边长分别为3和4,下列说法正确的是( )
A.斜边长为25 B.三角形周长为25
C.斜边长为5 D.三角形面积为20
4.在中, ,
(1)如果a=3,b=4,则c= ;
(2)如果a=6,b=8,则c= ;
(3)如果a=5,b=12,则c= ;
(4) 如果a=15,b=20,则c= .
5.如图,三个正方形中的两个的面积S1=25,S2=144,则另一个的面积S3为_______
课堂练习:
1.直角三角形中,以直角边为边长的两个正方形的面积为7,8,则以斜边为边长的正方形的面积为_________.
2.如图一个圆柱,底圆周长6cm,高4cm,一只蚂蚁沿外
壁爬行,要从A点爬到B点,则最少要爬行 cm
3.小雨用竹杆扎了一个长80cm、宽60cm的长方形框架,由于四边形容易变形,需要用一根竹杆作斜拉杆将四边形定形,则斜拉杆最长需________cm .
4.小杨从学校出发向南走150米,接着向东走了360米到九龙山商场,学校与九龙山商场的距离是 米.
5.已知直角三角形两直角边长分别为5和12, 求斜边上的高.
6.利用四个全等的直角三角形可以拼成如图所示的图形,这个图形被称为弦图.观察图形,验证:c2=a2+b2.
7.如图,小李准备建一个蔬菜大棚,棚宽4m,高3m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请计算阳光透过的最大面积.
8.下面是数学课堂的一个学习片段, 阅读后, 请回答下面的问题:
学习勾股定理有关内容后, 张老师请同学们交流讨论这样一个问题: “已知直角三角形ABC的两边长分别为3和4, 请你求出第三边.”
同学们经片刻的思考与交流后, 李明同学举手说: “第三边长是5”; 王华同学说: “第三边长是.” 还有一些同学也提出了不同的看法……
(1)假如你也在课堂上, 你的意见如何 为什么
(2)通过上面数学问题的讨论, 你有什么感受 (用一句话表示)
9.蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)
10.已知:如图,△ABC中,AB>AC,AD是BC边上的高.
求证:AB2-AC2=BC(BD-DC).
课后练习:
1.已知直角三角形中30°角所对的直角边长是cm,则另一条直角边的长是( )
A. 4cm B. cm C. 6cm D. cm
2.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42 B.32 C.42 或 32 D.37 或 33
3.一架25分米长的梯子,斜立在一竖直的墙上,这时梯足距离墙底端7分米.如果梯子的顶端沿墙下滑4分米,那么梯足将滑动( )
A. 9分米 B. 15分米 C. 5分米 D. 8分米
4. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草.
5. 在△ABC中,∠C=90°,(1)已知 a=2.4,b=3.2,则c= ;(2)已知c=17,b=15,则△ABC面积等于 ;(3)已知∠A=45°,c=18,则a= .
6. 一个矩形的抽斗长为24cm,宽为7cm,在里面放一根铁条,那么铁条最长可以是 .
7.小明想测量学校旗杆的高度,他采用如下的方法:先降旗
杆上的绳子接长一些,让它垂到地面还多1米,然后将绳子
下端拉直,使它刚好接触地面,测得绳下端离旗杆底部5米,
你能帮它计算一下旗杆的高度.
8.有一只鸟在一棵高4米的小树梢上捉虫子,它的伙伴在离该树12米,高20米的一棵大树的树梢上发出友好的叫声,它立刻以4米/秒的速度飞向大树树梢.那么这只鸟至少几秒才能到达大树和伙伴在一起.
9. 如图∠B=90 ,AB=16cm,BC=12cm,AD=21cm,CD=29cm
求四边形ABCD的面积.
10.如图,一个梯子AB长2.5 米,顶端A靠在墙AC上,这时
梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置
上,测得BD长为0.5米,求梯子顶端A下落了多少米?
18.2 勾股定理的逆定理(1)
预习练习:
1. 分别以下列四组数为一个三角形的边长:(1)3,4,5;(2)5,12,13;(3)8,15,17;(4)4,5,6.其中能构成直角三角形的有( )
A.4组 B.3组 C.2组 D.1组
2. 三角形的三边长分别为 a2+b2、2ab、a2-b2(a、b都是正整数),则这个三角形是()
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
3.如果把直角三角形的两条直角边同时扩大到原来的2倍,那么斜边扩大到原来的( )
A.1倍 B. 2倍 C. 3倍 D. 4倍
4. 下列各命题的逆命题不成立的是( )
A.两直线平行,同旁内角互补 B.若两个数的绝对值相等,则这两个数也相等
C.对顶角相等 D.如果a=b,那么a2=b2
5.五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是( )
A B C D
课堂练习:
1.若△ABC的三个外角的度数之比为3:4:5,最大边AB与最小边BC的关系是_________.
2.若一个三角形的周长12cm,一边长为3cm,其他两边之差为cm,则这个三角形
是______________________.
3.将直角三角形的三边扩大相同的倍数后,得到的三角形是 ( ).
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不是直角三角形
4满足下列条件的三角形中,不是直角三角形的是( )
A.三个内角比为1∶2∶1 B.三边之比为1∶2∶
C.三边之比为∶2∶ D. 三个内角比为1∶2∶3
5.下列命题中是假命题的是( ).
A.△ABC中,若∠B=∠C-∠A,则△ABC是直角三角形.
B.△ABC中,若a2=(b+c)(b-c),则△ABC是直角三角形.
C.△ABC中,若∠A∶∠B∶∠C=3∶4∶5则△ABC是直角三角形.
D.△ABC中,若a∶b∶c=5∶4∶3则△ABC是直角三角形.
6.在△ABC中,,那么△ABC是( ).
A.等腰三角形 B.钝角三角形 C.直角三角形 D.等腰直角三角形
7.如图,四边形ABCD中,F为DC的中点,E为BC上一点,
且.你能说明∠AFE是直角吗?
8. 如图所示的一块地,已知AD=4m,CD=3m, AD⊥DC,AB=13m,BC=12m,求这块地的面积.
9. 一个零件的形状如左图所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如右图所示,这个零件符合要求吗?
10. 如图,E、F分别是正方形ABCD中BC和CD边上的点,且AB=4,CE=BC,F为CD的中点,连接AF、AE,问△AEF是什么三角形?请说明理由.
课后练习:
1.下列各组数据中,不能作为直角三角形三边长的是( )
A.9,12,15 B. C.0.2,0.3,0.4 D.40,41,9
2.已知三角形两边长为2和6,要使这个三角形为直角三角形,则第三边的长为( )
A. B. C. D.以上都不对
3. △ABC的三边分别是7、24、25,则三角形的最大内角的度数是 .
4.三边为9、12、15的三角形,其面积为 .
5.已知三角形ABC的三边长为满足,,则此三角形为
三角形.
6.在三角形ABC中,AB=12,AC=5,BC=13,则BC边上的高为AD= .
7. 如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,
求四边形ABCD的面积.
8. 如图,E、F分别是正方形ABCD中BC和CD边上的点,且AB=4,CE=BC,F为CD的中点,连接AF、AE,问△AEF是什么三角形?请说明理由.
9. 如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的
C处有一筐水果,一只猴子从D处上爬到树顶A处,
利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处
滑到地面B,再由B跑到C,已知两猴子所经路程都是15m,
求树高AB.
10. 观察下列勾股数:
第一组:3=2×1+1, 4=2×1×(1+1), 5=2×1×(1+1)+1;
第二组:5=2×2+1, 12=2×2×(2+1), 13=2×2×(2+1)+1;
第三组:7=2×3+1, 24=2×3×(3+1), 25=2×3×(3+1)+1;
第三组:9=2×4+1, 40=2×4×(4+1), 41=2×4×(4+1)+1;
……
观察以上各组勾股数的组成特点,你能求出第七组的各应是多少吗?第组呢?
18.2 勾股定理的逆定理(2)
预习练习:
1. 如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是( )
A.7,24,25 B.3,4,5 C.3,4,5 D.4,7,8
2.在下列说法中是错误的( )
A.在△ABC中,∠C=∠A一∠B,则△ABC为直角三角形.
B.在△ABC中,若∠A:∠B:∠C=5:2:3,则△ABC为直角三角形.
C.在△ABC中,若a=c,b=c,则△ABC为直角三角形.
D.在△ABC中,若a:b:c=2:2:4,则△ABC为直角三角形.
3. 有六根细木棒,它们的长度分别为2,4,6,8,10,12(单位:cm),从中取出三根首尾顺次连接搭成一个直角三角形,则这根木棒的长度分别为( )
A.2,4,8 B.4,8,10 C.6,8,10 D.8,10,12
4.将勾股数3,4,5扩大2倍,3倍,4倍,…,可以得到勾股数6,8,10;9,12,15;12,16,20;…,则我们把3,4,5这样的勾股数称为基本勾股数,请你也写出三组基本勾股数 , , .
5.若三角形的两边长为4和5,要使其成为直角三角形,则第三边的长为 .
课堂练习:
1.△ABC的三边分别为a=3cm,b=4cm,c=5cm,则△ABC中的最小角为_____。
2. 已知直角三角形的两边长分别为3、4,则第三边的平方为__________。
3.分别以下列四组数为一个三角形的边长:(1)6、8、10;(2)13、12、5;(3)1、2、3;
(4)4、5、6.其中能构成直角三角形的有( )
A.4组 B.3组 C.2组 D.1组
4. 已知△ABC的三边为a、b、c,有下列各组条件,判断△ABC的形状。
a=41,b=40,c=9;
5. 在△ABC中,AB=15,BD=14,AD=13,求BD边上的高AC。
6. 在四边形ABCD中, C是直角,AB=13,BC=4,CD=3,AD=12,求证:AD⊥BD
7.如图,已知等腰△ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,求△ABC的周长.
8.如图,三个村庄A、B、C之间的距离分别为AB=5km,BC=12km,AC=13km.要从B修一条公路BD直达AC.已知公路的造价为26000元/km,求修这条公路的最低造价是多少?
9.如图,AB为一棵大树,在树上距地面10m的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处上爬到树顶A处,利用拉在A处的滑绳AC,滑到C处,另一只猴子从D处滑到地面B,再由B跑到C,已知两猴子所经路程都是15m,求树高AB.
10.如图,在△ABC中,∠ACB=90 ,AC=BC,P是△ABC内的一点,且PB=1,PC=2,PA=3,求∠BPC的度数.
课后练习:
1.已知在一个三角形ABC中,BC=6,BC边上的高为7,若AC=5,则AC边上的高为 _________.
2.已知一个三角形的三边分别为3k,4k,5k(k为自然数),则这个三角形为______,理由是_______.
3.一个三角形的三边分别为7cm,24 cm,25 cm,则此三角形的面积为_________。
4.若一个三角形的三边之比为5:12:13,且周长为60cm,则它的面积为_________。 .
5.给出下列几组数:① ;②8,15,16;③n2-1,2n,n2+1;④m2-n2,2mn,m2+n2(m>n>0).其中—定能组成直角三角形三边长的是( ).
A.①② B.③④ C.①③④ D.④
6.下列各组数能构成直角三角形三边长的是( ).
A.1,2,3 B.4,5,6 C.12,13,14 D.9,40,41
7.等边三角形的三条高把这个三角形分成直角三角形的个数是( ).
A.8个 B.10个 C.11个 D.12个
8.如果一个三角形一边的平方为2(m2+1),其余两边分别为m-1,m + l,那么这个三角形是( );
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
9. 下列数组中,能组成一个直角三角形的有( )
(1) 15,20,25;(2)10,24,25;(3)9,80,81;(4)8,15,17
A.1组 B.2组 C.3组 D.4组
10.我们知道,以3,4,5为边长的三角形为直角三角形,称3,4,5为勾股数组,记为(3,4,5),类似地,还可得到下列勾股数组:(8,6,10),(15,8,17),(24,10,26)等.
(1)请你根据上述四组勾股数的规律,写出第六组勾股数;
(2)试用数学等式描述上述勾股数组的规律;
(3)请证明你所发现的规律.
第十八章《勾股定理》测试题
(时间:100分钟 总分:100分)
一、相信你一定能选对!(每小题3分,共24分)
1. 三角形的三边长分别为6,8,10,它的最短边上的高为( )
A. 6 B. 4.5 C. 2.4 D. 8
2. 下面几组数:①7,8,9;②12,9,15;③m2 + n2, m2–n2, 2mn(m,n均为正整数,mn);④,,.其中能组成直角三角形的三边长的是( )
A. ①② B. ②③ C. ①③ D. ③④
3. 三角形的三边为a、b、c,由下列条件不能判断它是直角三角形的是( )
A.a:b:c=8∶16∶17 B. a2-b2=c2
C.a2=(b+c)(b-c) D. a:b:c =13∶5∶12
4. 三角形的三边长为,则这个三角形是( )
A. 等边三角形 B. 钝角三角形 C. 直角三角形 D. 锐角三角形.
5.已知一个直角三角形的两边长分别为3和4,则第三边长是( )
A.5 B.25 C. D.5或
6.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是( )
A. 24cm2 B. 36cm2 C. 48cm2 D. 60cm2
7.直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )
A.121 B.120 C.90 D.不能确定
8. 放学以后,小红和小颖从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖20分钟到家,小红和小颖家的直线距离为( )
A.600米 B. 800米 C. 1000米 D. 不能确定
二、你能填得又快又对吗?(每小题3分,共24分)
9. 在△ABC中,∠C=90°, AB=5,则++=_______.
10. 如图,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成.如果图中大、小正方形的面积分别为52和4,那么一个直角三角形的两直角边的和等于 .
11.直角三角形两直角边长分别为5和12,则它斜边上的高为_______.
12.直角三角形的三边长为连续偶数,则这三个数分别为__________.
13. 如图,一根树在离地面9米处断裂,树的顶部落在离底部12米处.树折断之前有 米.
14.如图所示,是一个外轮廓为矩形的机器零件平面示意图,根据图中标出尺寸(单位:mm)计算两圆孔中心A和B的距离为 .
15.如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2米,梯子的顶端B到地面的距离为7米.现将梯子的底端A向外移动到A’,使梯子的底端A’到墙根O的距离等于3米,同时梯子的顶端 B下降至 B’,那么 BB’的值: ①等于1米;②大于1米5;③小于1米.其中正确结论的序号是 .
16.小刚准备测量河水的深度,他把一根竹竿插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,河水的深度为 .
三、认真解答,一定要细心哟!(共52分)
17.(5分)右图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试分别画出一条长度是有理数的线段和一条长度是无理数的线段.
18.(5分)已知a、b、c是三角形的三边长,a=2n2+2n,b=2n+1,c=2n2+2n+1(n为大于1的自然数),试说明△ABC为直角三角形.
19.(5分)小东拿着一根长竹竿进一个宽为3米的城门,他先横着拿不进去,又竖起来拿,结果竿比城门高1米,当他把竿斜着时,两端刚好顶着城门的对角,问竿长多少米?
20.(5分)如图所示,某人到岛上去探宝,从A处登陆后先往东走4km,又往北走1.5km,遇到障碍后又往西走2km,再折回向北走到4.5km处往东一拐,仅走0.5km就找到宝藏。问登陆点A与宝藏埋藏点B之间的距离是多少?
21.(5分)如图,将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和10㎝的长方体无盖盒子中,求细木棒露在盒外面的最短长度是多少?
22.(5分)印度数学家什迦逻(1141年-1225年)曾提出过“荷花问题”:
“平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅?”
请用学过的数学知识回答这个问题.
23.(5分)如图,甲乙两船从港口A同时出发,甲船以16海里/时速度向北偏东40°航行,乙船向南偏东50°航行,3小时后,甲船到达C岛,乙船到达B岛.若C、B两岛相距60海里,问乙船的航速是多少?
24.(5分)如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿
∠CAB的角平分线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
25.(6分)如图,铁路上A、B两点相距25km, C、D为两村庄,若DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.求E应建在距A多远处?
26.(6分)如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
第5题图
第7题图
第8题图
第9题图
5m
13m
第5题图
A
D
E
B
C
8
6
A
E
C
D
B
A
第5题图
S1
S2
S3
3m
4m
20m
D
A
C
C
B
A
D
第4题图
D
C
B
F
E
A
C
B
D
第7题图
F
E
A
C
B
D
第8题图
B
A
C
D
.
第9题图
D
B
C
A
B
12 5
C 路、 D..13 D A
B
A
C
D
.
A
C
P
B
60
1200
140
60
B
A
C
第10题图
第13题图
第14题图
第15题图
A
B
4
1.5
2
4.5
0.5
A
C
B
A
E
C
D
B
C
A
B
D
E
10
15
A
B
小河
东
北
牧童
小屋
